Neliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä. Kummalla on suurempi piiri, neliöllä vai ympyrällä?

Tähän ongelmaan on olemassa monta hieman erilaista ratkaisutapaa. Muiden muassa Pythagoraan lauseen, kehäkulmien ja keskuskulmien sekä trigonometrian peruskaavan kautta vastaus voidaan päätellä. Tässä esittelemäni ratkaisulinja nojaa puolestaan yhdenmuotoisiin kolmioihin, ja koska siihen liittyy eräs elegantti tulos, on se mielestäni erityisen kiinnostava. Alun perin tämä ongelma ratkaisuineen tuli vastaan Colin Beveridgen blogissa.

Täydennettään alkuperäistä kuvaa hieman. 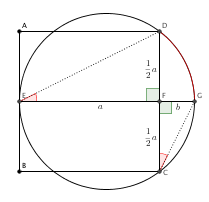Piirretään ympyrälle halkaisija , joka leikkaa neliön sivua pisteessä . Merkitään neliön sivun pituudeksi ja janan pituutta . Yhdenmuotoisissa kolmioissahan vastinosien pituuksien suhde säilyy. Kolmioiden yhdenmuotoisuuden osoittamiseksi riittää näyttää, että kolmioissa on kaksi yhtä suurta vastinkulmaparia. Kuvan kolmiot ja  ovat yhdenmuotoiset, sillä kulma  on molemmissa suora ja lisäksi molemmista kolmioista löytyy samaa kaarta  vastaavat kehäkulmat, jotka kehäkulmalauseen mukaan ovat yhtä suuret.

Nyt, koska vastinsivujen suhde säilyy, saadaan yhtälö , eli  josta , eli ympyrän halkaisija on -kertainen neliön sivuun verrattuna. Tästä seuraa se, että ympyrän piiri on , joka on hieman vähemmän kuin neliön piiri .

Minun mielestäni ratkaisun hienous perustuu juuri tähän yhdenmuotoisten kolmioiden käyttöön, sillä se tekee ratkaisusta hyvin lyhyen ja suoraviivaisen. Itse asiassa tässä hyödynnetään kaikille jännenelikulmioille yhteistä ominaisuutta: lävistäjien leikkauspiste jakaa lävistäjät siten, että leikkautuvien osien tulo on vakio. Tämä tulos saadaan välittömästi yhdenmuotoisista kolmioista, olipa jännenelikulmio millainen tahansa. Tulosta voi kokeilla oheisella Geogebra-appletilla pisteitä liikuttelemalla.