Kuvitellaan kaksi tuomioistuinta. Ensimmäisessä tuomioistuimessa istuu kolme tuomaria, joista kaksi osaa toisistaan riippumatta tehdä oikeudenmukaisen ratkaisun päätöksissään todennäköisyydellä ![]() . Kolmas tuomari heittää päätöksensä aina kolikolla. Ratkaisu saadaan enemmistöpäätöksellä. Toinen tuomioistuin koostuu vain yhdestä tuomarista, joka osaa tehdä oikean päätöksen todennäköisyydellä
. Kolmas tuomari heittää päätöksensä aina kolikolla. Ratkaisu saadaan enemmistöpäätöksellä. Toinen tuomioistuin koostuu vain yhdestä tuomarista, joka osaa tehdä oikean päätöksen todennäköisyydellä ![]() . Kumpi tuomioistuin antaa todennäköisemmin oikean tuomion?
. Kumpi tuomioistuin antaa todennäköisemmin oikean tuomion?
Ratkaisu: Molemmat tuomioistuimet ovat yhtä hyviä. Ensimmäisessä tuomioistuimessa on kolme mahdollista tapausta, joissa ratkaisu on oikeudenmukainen:
- Ensimmäinen ja toinen tuomari osuvat oikeaan. Tällöin lantinheittäjätuomarin ratkaisulla ei ole väliä. Todennäköisyys tälle on riippumattomuuden nojalla
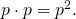
- Ensimmäinen on oikeassa, toinen väärässä ja lantinheittäjä oikeassa. Todennäköisyys tälle on
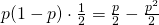 .
. - Ensimmäinen erehtyy, toinen on oikeassa ja lantinheittäjä on oikeassa. Tämänkin todennäköisyys on
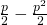 .
.
Koska tapaukset ovat erillisiä, on tuomioistuimen onnistumistodennäköisyys näiden kolmen tapauksen todennäköisyyksien summa, eli
![]()
Tämä pulma on Frederick Mostellerin kirjasta Fifty Challenging Problems in Probability with Solutions (Dover Publications, 1965).

