todennäköisyyslaskenta

2

Kolme rahakuorta

|

Seuraava pulma on jälleen Thomas Poveyn peruja. Se on sukua kuuluisalle Monty Hallin ongelmalle, mutta siinä on oma pieni lisämausteensa.

Saat kirjekuoren, jossa on tietty summa rahaa. Tämän jälkeen näytän sinulle kaksi muuta kuorta, joista toisessa on kaksinkertainen rahasumma ja toisessa puolet kirjekuoresi rahasummasta. Suljen kaksi muuta kuorta ja sekoitan ne niin, ettei niistä voi mitenkään päätellä, kumpi oli kumpi. Nyt sinulla on kaksi vaihtoehtoa: voit joko pitää nykyisen kuoresi tai vaihtaa jompaan kumpaan toisista kuorista. Mitä sinun kannattaisi tehdä?

Ratkaisu: Tutkitaan ongelmaa odotusarvon käsitteen kautta. Odotusarvo tarkoittaa eräänlaista satunnaisilmiön jakauman keskiarvoa, jota laskettaessa satunnaismuuttujan arvot painottuvat niiden todennäköisyyksien suhteessa.

Olkoon nyt kirjekuoressasi oleva rahasumma X. Näin ollen kahdessa muussa kuoressa olevat rahasummat ovat 2X sekä \frac{1}{2}X. Nyt on kaksi mahdollista tapausta.

  1. Et vaihda kuoria. Tällöin saamasi rahasumman odotusarvo on varmasti X.
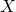  2. Vaihdat. Nyt voit todennäköisyydellä 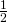\frac{1}{2} saada kuoren, jossa on 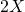2X, ja samoin todennäköisyydellä 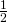\frac{1}{2} kuoren, jossa on 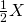\frac{1}{2}X. Saamasi rahasumman odotusarvo on nyt \frac{1}{2}\cdot 2X+\frac{1}{2}\cdot\frac{1}{2}X=\frac{5}{4}X.

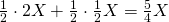Näin ollen vaihto kannattaa.

 

2

Laskut sekaisin

|

Kiireinen yrittäjä lähettää kuudelle asiakkaalleen laskun ja sulkee ne kirjekuoriin. Äkkiä hän huomaa, että osoitetarrat unohtuivat kuorien päältä. Millä todennäköisyydellä hän saa sattumanvaraisesti lätkimistään tarroista täsmälleen viisi oikeisiin kuoriin?

Kirjuri Ezra (n. 700-l.) Kuvalähde: Wikimedia Commons/Public domain

Kirjuri Ezra (n. 700-l.) Kuvalähde: Wikimedia Commons/Public domain

Ratkaisu: Todennäköisyys on nolla. Jos viisi osoitetta menee oikein, myös kuudes menee.

0

Kolikonheittoa shakkilaudalla

|

Pyöreä kolikko pudotetaan sattumanvaraisesti suurelle shakkilaudalle. Shakkilaudan ruudun sivu on kaksinkertainen kolikon halkaisijaan verrattuna. Millä todennäköisyydellä kolikko putoaa sekä mustan että valkean ruudun päälle?

Tämä hauska pikku pulma tuli vastaan Alex Bellosin The Guardianissa pitämää pulmapalstaa selatessani. Hän puolestaan sanoi löytäneensä ongelman kirjasta, jolla on hieno nimi: Professor Povey’s Perplexing Problems. Tämä Thomas Poveyn kirja lähtikin heti tilaukseen. Pitäkää siis varanne jatkossakin, rakkaat pulmakulman lukijat!

Ratkaisu: 

Tarkastellaan shakkilautaa, jonka ruudun sivun pituus on 2a. Tällöin kolikon halkaisija on a, ja kolikkoja mahtuu kerralla yhden ruudun sisälle neljä. Tässä asetelmassa kolikkojen keskipisteet muodostavat neliön, jonka sivun pituus on a. image

Jos nyt pudotamme kolikon shakkiruudulle, ei se ulotu toisen ruudun puolelle, mikäli sen keskipiste jää tummennetun neliön sisälle. Tämän tummennetun neliön ala on \frac{1}{4} koko ruudun alasta, joten vastaus kysymykseen on tietenkin \frac{3}{4}.

0

Lisää tyttöjä – ratkaisu

|

Eräässä teoreettisessa valtiossa haluttiin, että naisten osuus väestöstä kasvaisi. Niinpä valtion parlamentti hyväksyi lain, jonka mukaan kuhunkin perheeseen piti saada tyttölapsi. Jos perheeseen oli syntynyt tyttö, oli lasten hankkiminen lopetettava. Jos taas perheessä oli vain poikalapsia, oli lasten hankkimista jatkettava tytön syntymiseen asti. Oletetaan, että jokainen syntyvä lapsi on joko tyttö tai poika. Oletetaan myös, että tyttöjen ja poikien syntymätodennäköisyydet ovat samat. Kun populaation koko vähitellen tasoittuu, kuinka suureksi tyttöjen osuus syntyvistä lapsista kasvaa? Jatko-ongelmana voidaan pohtia, mikä on suurin mahdollinen tyttöjen osuus populaatiosta ja millä (riittävän humaaneilla) keinoilla se voidaan saavuttaa.

Ongelman ratkaisu on hyvin yksinkertainen, ja samalla saadaan vastaus myös jatko-ongelmaan. Jos nimittäin tyttöjen ja poikien syntymätodennäköisyydet ovat kuitenkin samat, on lapsista puolet tyttöjä ja puolet poikia, eikä suhde millään peukaloinnilla siitä muutu.

Asia voidaan järkeillä vielä vaikka seuraavasti. Perheiden ensimmäisistä lapsista puolet on tyttöjä, puolet poikia. Perheiden toisista lapsista puolet on tyttöjä ja puolet poikia. Perheiden kolmansista lapsista puolet on tyttöjä, puolet poikia. Ja niin edelleen. Puolet ja puolet.

0

Lisää tyttöjä

|

Eräässä teoreettisessa valtiossa haluttiin, että naisten osuus väestöstä kasvaisi. Niinpä valtion parlamentti hyväksyi lain, jonka mukaan kuhunkin perheeseen piti saada tyttölapsi. Jos perheeseen oli syntynyt tyttö, oli lasten hankkiminen lopetettava. Jos taas perheessä oli vain poikalapsia, oli lasten hankkimista jatkettava tytön syntymiseen asti. Toisin sanoen perheiden oli hankittava lapsia tytön syntymiseen asti.

Oletetaan, että jokainen syntyvä lapsi on joko tyttö tai poika. Oletetaan myös, että tyttöjen ja poikien syntymätodennäköisyydet ovat samat. Kun populaation koko vähitellen tasoittuu, kuinka suureksi tyttöjen osuus syntyvistä lapsista kasvaa? Jatko-ongelmana voidaan pohtia, mikä on suurin mahdollinen tyttöjen osuus populaatiosta ja millä (riittävän humaaneilla) keinoilla se voidaan saavuttaa.

Tämä pulma kuuluu tilastomatematiikan klassikkoihin. Viimeisimpänä sen tapasin The Guardianiin pähkinäpalstaa kirjoittavan Alex Bellosin videoblogista. Bellos on kirjoittanut kirjoja paitsi matematiikasta myös jalkapallosta, joten hän on sikälikin sangen fiksu heppu.

Ongelman ratkaisu on tässä.