Tehtävänäsi on pelata kolme erää squashia ja voittaa niistä kaksi peräkkäin. Vastaasi asettuu vuoron perään hyvä pelaaja ja kehno pelaaja. Kumpi vastustajista sinun kannattaa kohdata ensin? Eli kannattaako sinun pelata erät järjestyksessä hyvä–kehno–hyvä vai kehno–hyvä–kehno?
Ratkaisu: Parempi järjestys on hyvä–kehno–hyvä. Ratkaisua voidaan lähestyä ainakin kahdella tavalla. Ensinnäkin, koska tehtävänäsi on voittaa kaksi peräkkäistä erää, on sinun välttämättä voitettava eristä keskimmäinen. Sen voittotodennäköisyys kannattaa maksimoida, joten kehno pelaaja kannattaa kohdata nimenomaan silloin.
Ratkaisu voidaan toki osoittaa oikeaksi myös matemaattisesti. Olkoon todennäköisyys sille, että voitat hyvän pelaajan ![]() , ja kehnon pelaajan voittamiselle
, ja kehnon pelaajan voittamiselle ![]() . Nyt tietenkin
. Nyt tietenkin ![]() , eli hyvän pelaajan voittaminen on epätodennäköisempää kuin kehnon. Näillä merkinnöillä häviät hyvälle pelaajalle todennäköisyydellä
, eli hyvän pelaajan voittaminen on epätodennäköisempää kuin kehnon. Näillä merkinnöillä häviät hyvälle pelaajalle todennäköisyydellä ![]() ja kehnolle todennäköisyydellä
ja kehnolle todennäköisyydellä ![]() . Oletetaan, että peräkkäisten erien voittotodennäköisyydet eivät riipu toisistaan.
. Oletetaan, että peräkkäisten erien voittotodennäköisyydet eivät riipu toisistaan.
Erilaisia tapoja voittaa kaksi erää peräkkäin on kolme:
- voitto, voitto, voitto
- voitto, voitto, tappio
- tappio, voitto, voitto
Nämä ovat erillisiä, riippumattomia tapauksia, joten yhden tapauksen todennäköisyys saadaan tulon avulla ja kokonaistodennäköisyys laskemalla yksittäisten todennäköisyyksien summa. Tutkitaan ensin järjestys hyvä–kehno–hyvä. Tästä saadaan todennäköisyys
![]()
Vastaavasti järjestykselle kehno–hyvä–kehno saadaan todennäköisyys
![]()
Koska ![]() , niin
, niin ![]() , joten
, joten ![]() .
.
Tämäkin ongelma tuli vastaan Alex Bellosin pulmapalstan kautta. Bellos kreditoi pulman lähteeksi Frederick Mostellerin kirjan Fifty Challenging Problems in Statistics with Solutions. Tämä pulmablogiharrastus alkaa käydä kukkarolleni, sillä Mostellerin kirjan lisäksi nettikirjakaupasta tarttui (taas kerran) mukaan muutama muukin alan teos. Niistä luultavasti tuonnempana lisää.



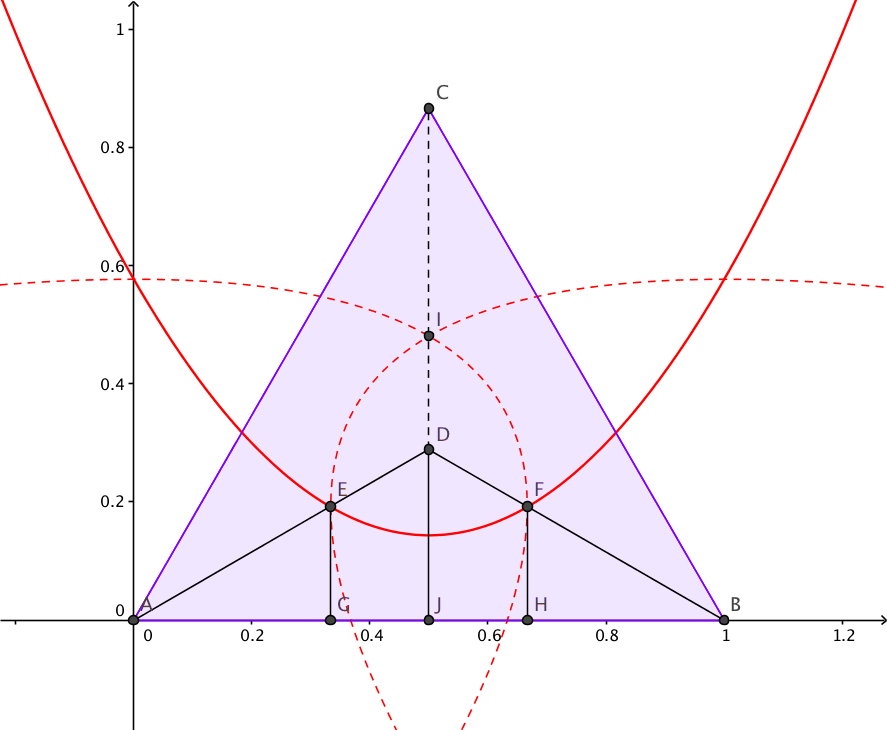 Yleisyydestä luopumatta voimme sijoittaa kolmion yhden kärjen origoon ja asettaa sivun pituudeksi
Yleisyydestä luopumatta voimme sijoittaa kolmion yhden kärjen origoon ja asettaa sivun pituudeksi ![Rendered by QuickLaTeX.com \[A_{EFGH}=\int_{\frac{1}{3}}^{\frac{2}{3}} \left(\sqrt{3}\left(x-\frac{1}{2}\right)^2+\frac{\sqrt{3}}{12}\right)dx=\frac{5}{54\sqrt{3}}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-22d13220cc06a67c90e684df193bc745_l3.png)
![Rendered by QuickLaTeX.com \[\frac{A_{ABD}-A_{AGE}-A_{EFGH}-A_{BHF}}{A_{ABD}}=\frac{\frac{\sqrt{3}}{12}-\frac{\sqrt{3}}{54}-\frac{5}{54\sqrt{3}}-\frac{\sqrt{3}}{54}}{\frac{\sqrt{3}}{12}}=\frac{5}{27}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-eea62c67a2ca7772f472cc09b2d53025_l3.png)


 On mahdollista, että neula joko putoaa reunan päälle tai sitten ei. Olkoon
On mahdollista, että neula joko putoaa reunan päälle tai sitten ei. Olkoon 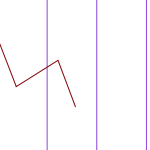 en, eli
en, eli 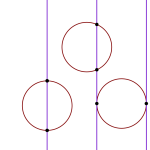 Neula, jonka pituus on
Neula, jonka pituus on 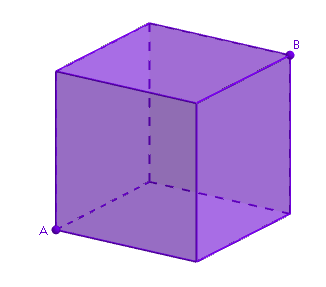 Muurahainen lähtee liikkeelle kuution kärjestä
Muurahainen lähtee liikkeelle kuution kärjestä