suhteellinen nopeus

0

Kärpänen – ratkaisu

|

Auto ajaa 60 km/h. Sitä vastaan lähtee 100 kilometrin päästä mopo, jonka nopeus on 40 km/h. Auton etupuskurilta lähtee samalla hetkellä lentoon kärpänen, joka lentää 80 km/h kohti mopoa. Kun kärpänen saavuttaa mopon, se lähtee takaisin kohti autoa, jonka luona se kääntyy välittömästi kohti mopoa ja niin edelleen. Kuinka pitkän matkan kärpänen ehtii lentää ennen kuin auto ja mopo kohtaavat?

Auto ja mopo kohtaavat tunnin kuluttua lähdöstä. Siis kärpänen lentää 80 kilometriä. Kuten eräs vakiokommentaattori Twitterissä totesi, kannattaisi ehkä uskoa vähitellen #viikonhelppo-tunnistetta. Toki tämän ongelman voi ehkä ratkoa jollakin hankalammallakin tavalla…

Niin, ja ilmeisesti ongelmassa hämäsi myös sen epäluonnollisuus. Minulle valistettiin, että kärpäsen lentonopeus on oikeastaan noin 8 km/h. Mutta tämä olikin matemaattinen erikoiskärpänen. Pistemäinen, ja niin edelleen.

0

Juokseva koira – ratkaisu

|

Koira lähtee juoksemaan vakionopeudella 50 metriä pitkän jonon perältä kohti jonon kärkeä. Jono lähtee samaan aikaan liikkeelle, myös vakionopeudella. Kun koira saavuttaa jonon kärjen, se kääntyy välittömästi takaisin (oletetaan siis, että tähän ei kulu aikaa) ja jatkaa matkaansa samalla vakionopeudella kohti jonon häntää. Kun koira saavuttaa jonon hännän, on jono edennyt 50 metriä. Kuinka pitkän matkan koira juoksi?

Juoksevan koiran ongelman ratkaiseminen vaatii hieman yksinkertaista ymmärrystä fysiikasta (mikä kuvaa täsmälleen omaa tasoani) sekä lievää luovuutta käytettävien yksiköiden kanssa. Päärooli on nopeuden, matkan ja ajan välisellä perusyhteydellä 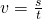v=\frac{s}{t}, josta saadaan, että aika 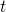t voidaan ilmaista t=\frac{s}{v}.

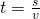Aletaan ensin muokata käytettäviä yksiköitä meille sopiviksi. Olkoon 50 metriä 1 ”matka” ja olkoon ajan 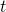t yksikkönä ”aika, joka jonolta kuluu 1 matkan kulkemiseen”. Tällöin jonon nopeutta voidaan merkitä 1:llä.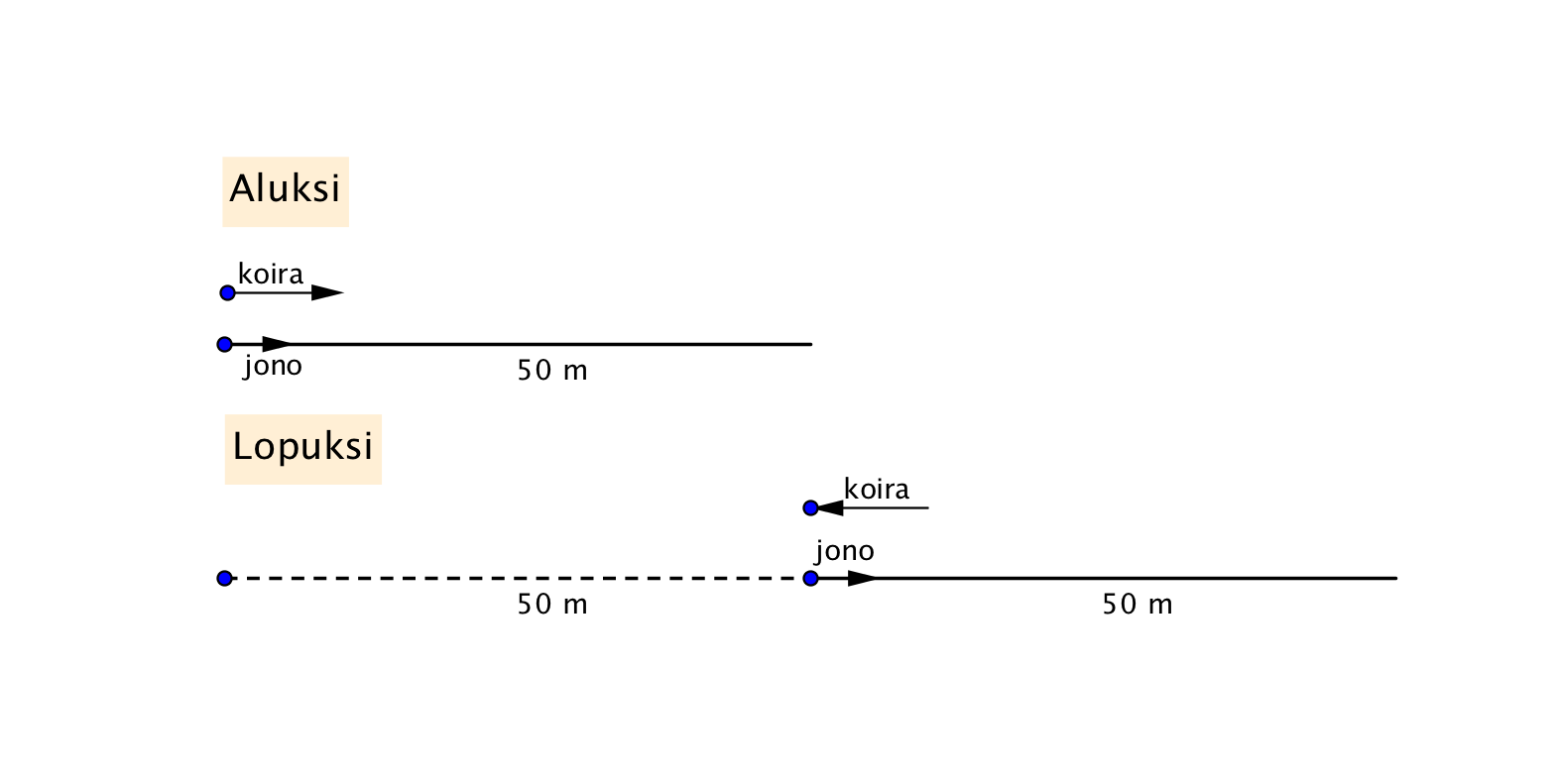koiranratkaisuTutkitaan sitten koiran juoksemiseen kuluvaa aikaa. Jaetaan aika kahteen osaan, jonon kärjen saavuttamiseen 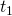t_1 ja jonon hännille palaamiseen 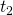t_2. Nyt siis 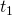t_1 on aika, jossa koira juoksee 50 metriä (eli yhden ”matkan”) jonoa enemmän. Merkitään koiran nopeutta  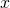x, jolloin sen nopeus suhteessa jonoon on 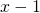x-1. Näin ollen 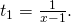t_1=\frac{1}{x-1}. Vastaavasti paluumatkalla koiran nopeus suhteessa jonoon on 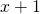x+1, joten 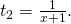t_2=\frac{1}{x+1}. 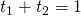Koska t_1+t_2=1, saadaan yhtälö, joka ratkaisee ongelman: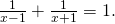  \frac{1}{x-1}+\frac{1}{x+1}=1.

Yhtälö saadaan muokattua muotoon 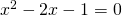x^2-2x-1=0. Tämän yhtälön juurista 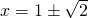x=1\pm\sqrt{2} vain positiivinen vaihtoehto 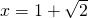x=1+\sqrt{2} hyväksytään. Koiran nopeus on siis  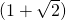(1+\sqrt{2}) 50 metrin matkaa ajassa, joka jonolta 50 metriin kuluu, joten ongelman vastaus on  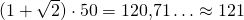(1+\sqrt{2})\cdot 50=120,71\ldots\approx 121 metriä.

Juoksevan koiran ongelma johtaa toiseen, hieman haastavampaan pulmaan: mitäpä, jos koira juoksisikin neliön muotoisen marssimuodostelman ympäri? Jos neliön sivu olisi 50 metriä ja muodostelma etenisi 50 metriä, kuinka pitkän matkan koira juoksisi? Ratkaisussa tarvittava yhtälö on vain hieman monimutkaisempi kuin tässä esitelty. Kokeilepa ratkaista, ja kerro tuloksistasi vaikkapa tämän blogin kommenttiosioon!