Kollegani Petri Kuukkanen antoi minulle melkoisen pirulaisen ratkottavaksi. Näin se kuuluu:
Järjestä luvut ![]() lukujonoksi
lukujonoksi ![]() niin, että
niin, että
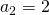 ja
ja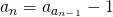 , kun
, kun 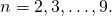
Ratkaisu: Pulma on varsin originaali, en ole törmännyt aiemmin tällaiseen, eikä ole Petrikään, joka pulman on laatinut. Hän on myös tarkastanut, ettei pulmaan löydy kuin yksi ratkaisu. Tietenkinhän pulma voidaan ratkoa myös kokeilemalla, mahdollisia järjestyksiä on vain ![]() kappaletta, mutta mekaaninen ratkaisu olisi vähän tylsä. Mennään siis loogisella päättelyllä tekemääni ratkaisuun.
kappaletta, mutta mekaaninen ratkaisu olisi vähän tylsä. Mennään siis loogisella päättelyllä tekemääni ratkaisuun.
Poimitaan helpot ensin. Jo tehtävänanto lupaa, että ![]() . Tästä seuraa heti, että
. Tästä seuraa heti, että ![]()
Seuraavaksi joudutaan jo vähän pohtimaan. Koska rekursiokaavan mukaan ![]() , kun
, kun ![]() , on
, on ![]() Koska
Koska ![]() kuuluu rekursiokaavan ulkopuolelle, on tehtävä johtopäätös, että koko jonon suurin termi on
kuuluu rekursiokaavan ulkopuolelle, on tehtävä johtopäätös, että koko jonon suurin termi on ![]() . Tämän perusteella puolestaan ratkeaa, että
. Tämän perusteella puolestaan ratkeaa, että ![]() Edelleen, koska
Edelleen, koska ![]() , saadaan termiksi
, saadaan termiksi ![]() .
.
Järjestämättä ovat vielä arvot ![]() ja
ja ![]() termeiksi
termeiksi ![]() ja
ja ![]() . Koska
. Koska ![]() ja koska
ja koska ![]() , niin
, niin ![]() . Nyt minulle tuli hetkeksi tenkkapoo, ja myönnänkin edenneeni seuraavaan vaiheeseen arvaamalla1. Käytettävissä olevien lukujen nojalla tämä jättää vaihtoehdot
. Nyt minulle tuli hetkeksi tenkkapoo, ja myönnänkin edenneeni seuraavaan vaiheeseen arvaamalla1. Käytettävissä olevien lukujen nojalla tämä jättää vaihtoehdot ![]() tai
tai ![]() . Näistä vaihtoehto
. Näistä vaihtoehto ![]() johtaa ristiriitaan (kokeile vain!).
johtaa ristiriitaan (kokeile vain!).
Kun ![]() , on edellä olleen yhtälön nojalla
, on edellä olleen yhtälön nojalla ![]() . Nyt myös
. Nyt myös ![]() ja vielä
ja vielä ![]() .
.
Koko jono on siis
![]()

