ratkaisut

0

Kaksi jokilaivaa – ratkaisu

|

Kaksi jokilaivaa lähtee samaan aikaan joen vastakkaisilta rannoilta tasaisella nopeudella suoraviivaisesti kohti vastarantaa; toinen laivoista on nopeampi. Kun laivat kohtaavat, on lähempi ranta 720 metrin päässä. Molemmat laivat pysähtyvät rannalle kymmeneksi minuutiksi, ja kun ne kohtaavat seuraavan kerran, ovat ne 400 metrin päässä toisesta rannasta. Kuinka leveä joki on?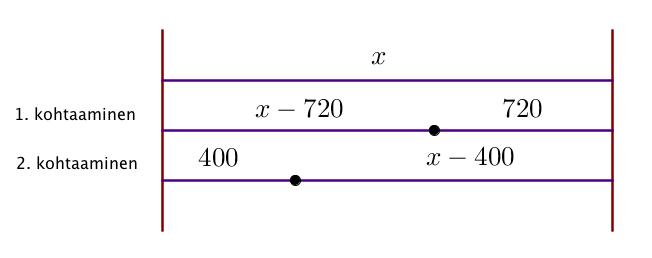Kaksi jokilaivaa

Olkoon joen leveys x metriä. Kumpikin laiva pysähtyy kymmeneksi minuutiksi, joten tällä ei ole merkitystä ratkaisun kannalta. Voidaan keskittyä pelkästään joella kulutettuun aikaan. Koska laivat kulkevat tasaisella nopeudella, ovat kuljettu matka ja käytetty aika suoraan verrannolliset. Tämä johtaa pariin melko yksinkertaiseen ratkaisumalliin.

Ensinnäkin, kun laivat kohtaavat ensimmäisen kerran, ovat ne taittaneet matkaa yhteensä x metriä. Toisen kohtaamisen hetkellä matkaa on taitettu puolestaan 3x metriä (molemmat laivat kertaallen koko välin ja vajaan toisen välin), joten kulutettu aikakin on kolminkertainen. Nopeamman laivan kulkemaa matkaa tutkimalla tästä saadaan yhtälö

    \[3(x-720)=2x-400,\]

jonka ratkaisu x=1760 (metriä) on joen leveys.

Toisaalta matkan ja käytetyn ajan verrannollisuus johtaa myös laivojen kulkemista matkoista laadittuun verrantoyhtälöön 

    \[\frac{x-720}{720}=\frac{2x-400}{x+400},\]

 josta nimittäjät pois kertomalla ja termejä järjestelemällä saadaan x^2-1760x=0. Tämän yhtälön positiivinen juuri on tietenkin sama x=1760.

2

Tiukka tennisottelu – ratkaisu

|

Tennisottelu kestää täydet viisi erää. Toisen pelaajan erissä voittamat pelit muodostavat aritmeettisen jonon. Kumpi voitti ottelun, kun kumpikin pelaajista voitti yhtä monta peliä?

Aritmeettisella jonolla tarkoitetaan lukujonoa, jossa peräkkäisten termien erotus on vakio. Siis esimerkiksi parilliset positiiviset kokonaisluvut muodostavat aritmeettisen jonon (2,4,6,\ldots), mutta kakkosen potenssit (1,2,4,8,\ldots) eivät.

Tennisottelussa erän voittamiseen tarvitaan yleensä 6, joskus 7 ja ainoastaan viidennen erän ollessa kyseessä mahdollisesti enemmän kuin 7 voitettua peliä. Siispä mikäli ”aritmeettinen” pelaaja voittaisi ottelun, olisi hänen voitettava erissä 6, 7 ja 8 peliä. Näin ollen hänen erissä voittamiensa pelien jono olisi välttämättä 4, 5, 6, 7, 8. Näin ollen voidaan pitää varmana, että erien tulokset ovat 4–6, 5–7, 6–X, 7–Y ja 8–6, missä 0\leq X\leq 4 ja Y=5 tai Y=6. Näissä tapauksissa aritmeettinen pelaaja voittaisi 30 peliä ja vastapelaaja 19+X+Y peliä, mikä selvästi on mahdotonta. Siis aritmeettinen pelaaja ei voi voittaa.

Minkälaisin pistein aritmeettinen pelaaja sitten voi hävitä ottelun? Voittaakseen kaksi erää neljästä ensimmäisestä hänen on saavutettava niissä 6 ja 7 voitettua peliä. Kävisikö 7, 6, 5, 4, 3? Tällöin ottelun tulos voisi olla A–7, B–6, 7–5, 6–4, 6–3. Koska aritmeettinen pelaaja voittaisi tässä mallissa 25 peliä ja koska A=5 tai A=6, voi B olla vastaavasti joko 1 tai 0. Mahdollisia ratkaisuja ovat siis ainakin 5–7, 1–6, 7–5, 6–4, 6–3 ja 6–7, 0–6, 7–5, 6–4, 6–3. Toisinpäin tämä tulosjono ei toimi – aritmeettinen ei siis voi ensin alkaa hävitä eriä.

Vai voiko sittenkin? Itse asiassa voi, mutta tällöin tarvitaan aritmeettinen jono 4, 5, 6, 7, 8. Tämä johtaa loppupisteisiin 6–4, 7–5, 1–6, 6–7, 10–8 tai 6–4, 7–5, 2–6, 5–7, 10–8. Erikoistapauksena siis viidennessä erässä ei pelata tie-breakia, joten sen erän voi hävitä myös 8 peliä voitettuaan.

Jos otetaan lukuun erikoistapaus, jossa vakiojono lasketaan aritmeettiseksi, saadaan vielä seuraavankaltainen tulossarja: 4–6, 4–6, 7–6, 7–6, 8–6. Tässä neljän ensimmäisen erän tulokset ovat järjestettävissä mihin tahansa järjestykseen, joten kaikkiaan tennisotteluongelmaan on 10 ratkaisua – joissa kaikissa voittajaksi selviytyy ei-aritmeettinen pelaaja. Tennistä pelatessaan kannattaa siis jättää lukujonot syrjään ja treenata esimerkiksi ykkössyöttö kuntoon!