peliteoria

0

Sata lanttia

|

Antti ja Petri pelaavat kiehtovaa rahapeliä: he ovat asettaneet sata kolikkoa riviin ja alkavat nostaa niitä yksi kerrallaan itselleen. Kolikot ovat kaikenlaisia viisisenttisistä kahden euron arvoisiin ja ne ovat satunnaisessa järjestyksessä. Sääntöihin kuuluu, että vuorollaan saa ottaa vain rivin reunimmaisen kolikon; kummasta tahansa päästä riviä saa nostaa.  Pelin voittaa se, kumpi saa kerättyä enemmän rahaa.

Antti aloittaa. Osoita, että Antti voi kerätä aina vähintään yhtä paljon rahaa kuin Petri.

Kuva: Branko Collin / Flickr (CC BY-SA 2.0)

Kuva: Branko Collin / Flickr (CC BY-SA 2.0)

Ratkaisu: Numeroidaan kolikot yhdestä sataan. Antti voi halutessaan varmasti poimia kaikki parilliset tai kaikki parittomat kolikot, sillä hänen haluamansa järjestysluku löytyy varmasti aina joko jonon kärjestä tai hänniltä. Niinpä hänen riittää aluksi vain katsoa, kummat kolikot kannattaa valita.

Jos kolikoita olisi yksi enemmän, etu voi siirtyä Petrille, vaikka hän saisikin yhden kolikon vähemmän kuin Antti. Jos parillisten ja parittomien arvojen ero on suurempi kuin Antin ensimmäisen kolikon arvo, 101 kolikon pelissä Petri ei ainakaan häviäisi.

0

Hyvät, pahat ja rumat

|

Sergio Leonen lännenelokuvan Hyvät, pahat ja rumat (1966) loppukohtauksessa Clint Eastwood, Lee Van Cleef ja Eli Wallach käyvät kuuluisan kolmintaistelun hautausmaalla, jonka asetelma on myös matemaattisesti kiintoisa: tällaisessa tilanteessahan nopein vetäjä ei automaattisesti olekaan vahvimmilla. Tarvitaan jonkinlaista optimointistrategiaa, jota voidaan mallintaa todennäköisyyslaskennan keinoin.

Kuva: Jacques Meynier de Malviala / Flickr (CC BY-NC-ND 2.0)

Kuva: Jacques Meynier de Malviala / Flickr (CC BY-NC-ND 2.0)

Leonen elokuvassa käsikirjoitus tietysti sanelee lopputuloksen, mutta kokeillaanpa kolmintaistelua tiukemmilla säännöillä. Arvotaan ensin ampumisjärjestys ja noudatetaan sitä loppuun asti. Ammutaan vuorojärjestyksessä yksi kuti kerrallaan minne tahansa, kunnes pystyssä on enää yksi mies. Oletetaan, että Clint osuu kohteeseensa aina, Lee 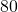80 prosentin varmuudella ja Eli 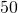50 prosentin varmuudella. Oletetaan vielä, että kaikki noudattavat parasta strategiaa, ja että kehenkään ei osu vahinkokimmokkeita. Kuka kolmikosta on todennäköisin taistelun voittaja? Mitkä ovat kunkin miehen täsmälliset selviytymismahdollisuudet?

Ongelman löysin jälleen Martin Gardnerin kautta; hän kertoo, että se on esiintynyt useissa lähteissä ainakin 1930-luvun lopulta alkaen.

Ratkaisu: Todennäköisin ammuskelun henkiinjäänyt on Eli. Hänelle paras strategia on ammuskella ilmaan siihen asti, kunnes jäljellä on vain toinen vastapelureista, sillä he tähtäävät varmasti toisiaan niin kauan kuin heissä henki pihisee, ja hyökätä sitten henkiinjääneen kimppuun. Mutta käydään nyt kunkin pyssysankarin mahdollisuudet läpi.

Clintin henkiinjäämisprosentti on helppo selvittää. Jos hän aloittaa Leetä vastaan, hän ampuu tämän. Jos taas Lee aloittaa, on Clintillä 20 prosentin mahdollisuus selvitä. Koska nämä tapaukset ovat erilliset ja yhtä todennäköiset, on Clintin selviämismahdollisuus Leetä vastaan 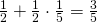\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{5}=\frac{3}{5}. Koska tämän jälkeen Clint selviää 50 prosentin todennäköisyydellä Elin laukauksesta, joten kaikkiaan Clintin eloonjäämistodennäköisyys on \frac{3}{5}\cdot\frac{1}{2}=\frac{3}{10}=30\%.

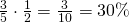Lee selviytyy voittajana Clintiä vastaan todennäköisyydellä 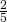\frac{2}{5}. Tämän jälkeen hän ajautuu kaksintaisteluun Elin kanssa. Jos hän selviytyy Elin ensimmäisestä laukauksesta, voittaa hän 80 prosentin todennäköisyydellä. Tämän jälkeen hän voi voittaa toisella laukauksellaan, ellei Eli osu, ja edelleen kolmannella, neljännellä, viidennellä laukauksella, kunnes ratkaisu tulee. Ensimmäisen laukauksen voiton todennäköisyys on 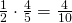\frac{1}{2}\cdot\frac{4}{5}=\frac{4}{10}, toisen laukauksen 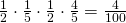\frac{1}{2}\cdot\frac{1}{5}\cdot\frac{1}{2}\cdot\frac{4}{5}=\frac{4}{100} ja niin edelleen. Kaikkiaan Leen voittomahdollisuudet mittelössä Elin kanssa muodostavat geometrisen summan

    \[\frac{4}{10}+\frac{4}{100}+\frac{4}{1000}+\frac{4}{10000}+\cdots\]

Tämä taas voidaan ilmoittaa päättymättömänä desimaalikehitelmänä 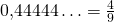0,44444\ldots=\frac{4}{9}. Lee siis voittaa Elin todennäköisyydellä \frac{4}{9}, joka yhdistettynä voittotodennäköisyyteen Clintiä vastaan antaa Leen kokonaistodennäköisyydeksi selvitä \frac{2}{5}\cdot\frac{4}{9}=\frac{8}{45}\approx 17,8\%.

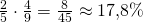Elin voittotodennäköisyys on nyt 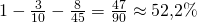1-\frac{3}{10}-\frac{8}{45}=\frac{47}{90}\approx 52,2\% ja siis selvästi paras kolmesta.

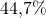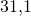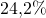Jos Eli ei paukuttelisikaan ilmaan, vaan tähtäisi vaarallisimpaan vastustajaansa vuorollaan alusta asti, hänen selviämismahdollisuutensa olisi noin 44,7\%. Tällöin Leen mahdollisuudet nousisivat 31,1 prosenttiin ja Clintin mahdollisuudet olisivat vain noin 24,2\%.