logiikka

0

Monivalintakysymys

|

Jos vastaat tähän kysymykseen sattumanvaraisesti, millä todennäköisyydellä vastaat oikein?

  1. 25 %
  2. 50 %
  3. 60 %
  4. 25 %

Tämä kysymys on kierrellyt jo jonkin aikaa ympäri nettiä. Kiitos kontribuutiosta, Mikko Saari!

Ratkaisu: Pulmaa ei tietenkään voida ratkaista sen itseensä viittaavan luonteen vuoksi. Toisin sanoen pulma ei ole hyvin määritelty. Se ei tietenkään tarkoita sitä, etteikö se olisi hauska. Juuri tällaisista paradokseista ja kielivitseistä minä olen pitänyt koko ikäni. Lisää tästä teemasta löytyy esimerkiksi Alexander Bogomolnyn mainiolta Cut the Knot -sivustolta.

0

Hullun loogikon vangit

|

Petri ja Eemil joutuivat hullun loogikon vangeiksi. Heidät suljettaisiin tuota pikaa selleihin, ja kummallekin annettaisiin ainoastaan virheetön kolikko. Heidän molempien pitäisi heittää tunnin ajan kerran minuutissa kolikkoa, siis yhteensä 60 kertaa. Kunkin heiton jälkeen he joutuisivat veikkamaan, saiko toinen herroista kruunan vai klaavan. Ja jos edes kerran molemmat olisivat yhtä aikaa oikeassa veikkauksessaan, hullu loogikko tappaisi heidät molemmat!

Ennen lopullista selleihin lukitsemista Petri ja Eemil saisivat keskustella keskenään vielä kymmenen minuutin ajan, mutta selleihin päädyttyään heillä ei olisi minkäänlaisia mahdollisuuksia kommunikoida keskenään. Oman kolikkonsa he toki näkisivät.

Viikon vaikea pulma on yrittää pelastaa Petrin ja Eemilin henki.

Kuva: Tom Blackwell/Flickr (CC BY-NC 2.0)

Kuva: Tom Blackwell/Flickr (CC BY-NC 2.0)

Ratkaisu: Petri ja Eemil voivat pelastua hyvin yksinkertaisella tempulla. Jos Petri veikkaa Eemilille aina samaa tulosta kuin oma heittonsa ja Eemil puolestaan vastakkaista Petrille, saavat he jokaisella heittokerralla täsmälleen yhden oikean arvauksen. Mahdollisia tapauksia on vain neljä, ja ne ovat tässä:

  1. Petri saa kruunan, veikkaa kruunaa. Eemil saa kruunan, veikkaa klaavaa. Petri on oikeassa, Eemil väärässä.
  2. Petri saa kruunan, veikkaa kruunaa. Eemil saa klaavan, veikkaa kruunaa. Petri on väärässä, Eemil oikeassa.
  3. Petri saa klaavan, veikkaa klavaa. Eemil saa kruunan, veikkaa klaavaa. Petri on väärässä, Eemil oikeassa.
  4. Petri saa klaavan, veikkaa klaavaa. Eemil saa klaavan, veikkaa kruunaa. Petri on oikeassa, Eemil väärässä.

Tämä pulma oli Alex Bellosin Monday Puzzle -palstalta The Guardianista.

4

Jännä jono

|

Aikakauslehtien pulmapalstoilta löytyy silloin tällöin tehtäviä, joissa täytyy jatkaa loogisesti annettua lukujonoa. Periaatteessa näissä tehtävissä ei ole päätä eikä häntää, sillä ellei äärettömäksi tarkoitetun jonon muodostamissääntöä ole annettu, voidaan sitä jatkaa millä tavalla tahansa. Siis valideja jatkotapoja jonolle 2, 4, 8,\ldots olisivat 16, 32, 64,\ldots yhtä hyvin kuin 90, 0, 22, \ldots. Kysymyksen muotoilun pitäisikin siis olla, että millä säännöllä kyseinen jono voidaan muodostaa ja miten se sillä säännöllä jatkuisi.

Mutta eipä takerruta liikaa tähän semantiikkaan. Yksi suosikkijonoistani alkaa

    \[13, 1113, 3113, 132113,\ldots\]

Viikon vaikea kysymys on, kuinka sitä jatketaan loogisesti.

Ratkaisu: Jono jatkuu 1113122113, 311311222113, \ldots eli aivan kuten kommentoijamme Mikko tuossa alla jo toteaakin. Kyseessä on niin kutsuttu ”sano mitä näet”-jono, eli logiikka taustalla on sanoa, mitä jonon edellisessä termisasä on. Näin ollen termiä 13 seuraa yksi ykkönen ja yksi kolmonen, siis 1113. Tämän jälkeen tulee kolme ykköstä ja yksi kolmonen, eli 3113. Sitten yksi kolmonen, kaksi ykköstä, yksi kolmonen, eli 132113. Ja niin edelleen.

Lukujonoista kiinnostuneiden aarreaitta on Neil Sloanen jo 1960-luvulta asti ylläpitämä tietokanta The On-Line Encyclopedia of Integer Sequences eli OEIS, joka löytyy osoitteesta oeis.org. Sieltä löytyy ”ihan kaikki”, ja sivusto päivittyy yhä aktiivisesti. Tämän pulman lukujono löytyy sieltä koodilla A006715.

2

Rehdit, retkut ja normaalit

|

Loogisten arvoitusten erikoismiehen Raymond Smullyanin kirjassa Mikä tämän kirjan nimi on? (Terra Cognita 2003, suom. Hannele Salminen) tutkitaan usein rehtejä, jotka puhuvat aina totta, ja aina valehtelevia retkuja. Joissakin ongelmissa mukana on myös kolmas kasti: normaalit, joista ei voi olla varma, puhuvatko he totta vai valehtelevatko. Niin myös tässä hauskassa pulmassa.

Rehtien, normaalien ja retkujen yhteisössä vallitsee tiukka kastijako. Rehdit ovat ylintä kastia, normaalit keskikastia ja retkut alinta kastia. Antti ja Tuomo esittävät seuraavat repliikit:

Antti: ”Olen alempaa kastia kuin Tuomo.”

Tuomo: ”Ei pidä paikkaansa!”

Voimmeko tästä päätellä, mihin kasteihin Antti ja Tuomo kuuluvat? Entä voimmeko päätellä, onko kumpikaan repliikeistä totta?

Ratkaisu: Antti ja Tuomo ovat normaaleja. Antti valehtelee, mutta Tuomo puhuu totta.

Antti ei voi olla rehti, sillä silloin hän ei voisi olla alempaa kastia kuin Tuomo. Jos Antti olisi retku, olisi hänen väitteensä valhetta, jolloin Tuomonkin olisi oltava retku. Tällöin taas Tuomon oma väittämä olisi totta, mikä on ristiriita retkuuden kanssa. Antin on siis oltava normaali.

Tuomo ei voi olla rehti, sillä silloin hän ei voisi totuudessa pysyen kiistää Antin väittämää. Jos taas Tuomo olisi retku, olisi hänen väittämänsä yhä ristiriidassa totuuden kanssa. Tuomo on siis totta puhuva normaali ja Antti normaali valehtelija.

0

Kössin syntymäpäivät

|

Pulmakulman ylläpidossa alkaa pian hyvin ansaittu kesäloma. Loma on kiireettömyyden ja rentoutumisen aikaa, ja niinpä juhlistammekin sitä pulmalla, jonka ajattelin laittaa tänne jo viime keväänä, kun koko sivusto oli vasta pilkkeenä silmäkulmassani. Se kiersi laajasti ympäri nettiä viime vuonna, mutta älkää nyt ihan vielä sieltä vastausta etsikö – ei se niin vaikea ole! Pulma oli Singapore and Asian Schools Maths Olympiad -kilpailun tehtävänä noin 15-vuotiaille koululaisille.

Kössillä on synttärit tulossa ja juhlat pitäisi järjestää, mutta Mikko ja Toni eivät valitettavasti tiedä, koska ne ovat. Pulmakulmaa pitkään seuranneella Kössillä on kuitenkin ketunhäntä kainalossaan. Hän paljastaa, että syntymäpäivä on jokin seuraavista:

  • 15., 16. tai 19. toukokuuta
  • 17. tai 18. kesäkuuta
  • 14. tai 16. heinäkuuta
  • 14., 15. tai 17. elokuuta

Sitten Kössi kuiskaa Mikolle oikean kuukauden ja Tonille oikean päivän. Loistavat loogikot Mikko ja Toni käyvät seuraavan keskustelun:

Mikko: ”En tiedä vastausta, mutta tiedän, ettei Tonikaan tiedä.”

Toni:  ”Ihan aluksi en minäkään tiennyt, mutta nytpä tiedän!”

Mikko: ”Ha! No niin tiedän minäkin!”

Milloin Kössin syntymäpäivä on?

Ratkaisu: Mikko voi oikean kuukauden kuultuaan poissulkea toukokuun ja kesäkuun, sillä 19. päivä on mahdollisuutena vain toukokuussa ja 18. päivä kesäkuussa. Jos Kössin syntymäpäivä olisi ollut jompi kumpi näistä, olisi Toni tiennyt sen heti ilman lisätietoa kuukaudesta.

Nyt Toni sai kuitenkin oivallista lisäinformaatiota siitä, mikä kuukausista on oikein. Ja koska sekä heinäkuussa että elokuussa on mahdollisena päivänä 14. päivä, ei se voi olla ratkaisu, jos Toni kerran tällä yhdellä lisävihjeellä ratkaisun selvitti. Jäljellä olevat vaihtoehdot ovat siis 15., 16. tai 17. päivä – kuukaudella ei Tonille ole enää merkitystä.

Mikko tietää oikean kuukauden, muttei päivää. Koska elokuulle jää kaksi vaihtoehtoa, mutta heinäkuulle enää yksi, on oikea syntymäpäivä välttämättä 16. heinäkuuta.

0

Kuulat purkissa

|

Purkissa on 75 valkoista kuulaa ja 150 mustaa kuulaa. Purkin vieressä on kasa mustia kuulia. Vähän tylsistynyt opettaja H. ottaa kuulia purkista seuraavilla säännöillä: hän nostaa silmät kiinni kaksi kuulaa ja katsoo, minkä värisiä ne ovat. Jos hän nostaa kaksi valkoista kuulaa, hän heittää ne pois ja laittaa purkkiin yhden mustan kuulan viereisestä kasasta. Jos taas hän nostaa ainakin yhden mustan kuulan, laittaa hän sen viereiseen kasaan ja palauttaa toisen kuulan takaisin purkkiin sen väristä riippumatta. Jokaisen nostokierroksen jälkeen purkissa on yksi kuula vähemmän kuin aiemmin. Lopulta purkkiin jää vain yksi kuula. Minkä värinen se on?

Kuva: Lenny Hirsch / Flickr (CC BY-NC-ND 2.0)

Kuva: Lenny Hirsch / Flickr (CC BY-NC-ND 2.0)

 

Ratkaisu: Purkin viimeinen kuula on valkoinen, sillä valkoiset kuulat poistuvat purkista vain pareittain.

0

Pimeät sukat

|

Pimeän vaatehuoneen sukkalaatikossa on 16 punaista sukkaa ja 20 sinistä sukkaa. Montako sukkaa minun pitää vähintään laatikosta ottaa, jotta saan varmasti parin samanvärisiä sukkia?

No. Tämä oli ihan liian helppo. Laitetaan vähän lisää panoksia. Laatikossa on yhtä monta sinistä ja punaista sukkaa. Tiedetään, että pienin määrä, joka sukkia pitää nostaa laatikosta, jotta saataisiin ainakin kaksi samanväristä sukkaa, on sama kuin määrä, joka pitää nostaa, jotta saataisiin varmasti kaksi eriväristä sukkaa. Montako sukkaa laatikossa on?

Ratkaisu: Ensimmäisen kysymyksen vastaus on kolme. Toisen kysymyksen vastaus on neljä.

0

Tuomaan talo

|

Tuomas asuu kadulla, jonka talonnumerot ovat väliltä 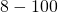8-100. Kössi tahtoo saada selville, mikä Tuomaan talon numero on.

Kössi kysyy, onko numero suurempi kuin 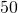50. Tuomas vastaa, mutta valehtelee.

Seuraavaksi Kössi kysyy, onko numero jaollinen neljällä. Tuomas vastaa, mutta valehtelee taas.

Sitten Kössi kysyy, onko numero jonkin luvun neliö. Nyt, kaikkien hämmästykseksi, Tuomas vastaa totuudenmukaisesti.

Kössi sanoo, että jos Tuomas vielä kertoisi, onko ensimmäinen numero 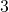3, hän tietäisi oikean talonnumeron. Tuomas vastaa Kössille, mutta emme tiedä, puhuiko hän totta. Tämän jälkeen Kössi ilmoittaa vastauksensa, joka valitettavasti on väärä.

Missä numerossa Tuomas oikeasti asuu?

Kuva: Bert Kaufmann/Flickr (CC BY-SA 2.0)

Kuva: Bert Kaufmann/Flickr (CC BY-SA 2.0)

Ratkaisu: Kössi ei tietenkään tiedä, että Tuomas puhuu suurimman osan ajasta puhdasta palturia. Siksi Kössi perustaa veikkauksensa siihen, mitä Tuomas vastaa, ja se puolestaan vie meidät ratkaisun jäljille.

Koska ensimmäiseen kysymykseen Tuomas valehteli ja lopuksi Kössi haluaa tietää, onko ensimmäinen numero 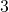3, on oikea talonnumero tietenkin suurempi kuin 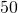50. Koska välillä 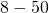8-50 on vain kaksi neljällä jaollista neliötä (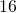16 ja 36) ja lukuisia sellaisia lukuja, jotka eivät ole joko jaollisia neljällä tai neliöitä tai kumpaakaan näistä, on Tuomas vastannut sekä neljälläjaollisuuskysymykseen (valheellisesti) että neliökysymykseen (todenmukaisesti) kyllä.

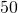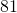Tämä kaikki tarkoittaa sitä, että todellisuudessa Tuomas asuu talossa, jonka numero on suurempi kuin 50, ei ole neljällä jaollinen ja on jonkin luvun neliö. Ainoa kyseeseen tuleva talonnumero on 81.

 

2

Lentävän hollantilaisen aarre

|
image

Johann Gehrts (1887): Lentävä hollantilainen/Wikimedia Commons (Public Domain)

Tämänkertainen viikon vaikea vie meidät merta edemmäs, tarkkaan ottaen Itämerta edemmäs, sillä pulma löytyi hollantilaiselta The Ultimate Puzzle Site -sivustolta.

Lentävä hollantilainen haaksirikkoutui, ja viiden merirosvon kopla on saanut haltuunsa 1000 kultarahan aarteen. Nämä eivät olekaan mitään aivan tavanomaisia piraatteja, vaan heillä kaikilla on kolme yhtenevää piirrettä:

  1. He ovat ahneita. He haluavat niin paljon rahaa kuin vain ikinä saavat.
  2. He ovat verenhimoisia. He vaikka tappavat toverinsa, jos hyötyvät siitä.
  3. He ovat täydellisen loogisia optimoijia. He tekevät aina itselleen tuottoisimmat päätökset.

Nyt merirosvojen pitäisi siis jakaa 1000 rahan aarre. He menettelevät seuraavasti. Merirosvot on järjestetty tiukkaan arvojärjestykseen ensimmäisestä viidenteen ja jokaisella merirosvolla on vuorollaan yksi mahdollisuus ehdottaa omasta mielestään sopivaa rahanjakoa. Jos enemmistö merirosvoista hyväksyy jaon, rahat jaetaan esityksen mukaan. Jos taas ehdotus ei saa enemmistöä taakseen, heitetään ehdottaja armotta yli laidan haita kuhisevaan mereen.

Mitä ensimmäinen merirosvo ehdottaa?

1

Loogiset lautapelaajat

|

Ystävykset Hannu, Mikko ja Tuomo pelaavat lautapeliä. Pystytkö selvittämään herrojen pelinappuloiden värit, kun tiedetään, että ne ovat punaiset, vihreät ja violetit, ja että seuraavista väittämistä täsmälleen yksi pitää paikkansa:

  • Hannu pelaa punaisilla.
  • Mikko ei pelaa punaisilla.
  • Tuomo ei pelaa violeteilla.
Kuva: Mikko Saari / Boardgamegeek (CC BY-NC-SA 3.0)

Kuva: Mikko Saari / Boardgamegeek (CC BY-NC-SA 3.0)

Tämä pulma taitaa olla yksi modernin lauselogiikan vanhimmista, ja sen on jossakin muodossa esittänyt jo logiikan ja tietokonearitmetiikan grand old man George Boole, jonka syntymästä tuli marraskuun 2015 alussa kuluneeksi 200 vuotta.

 

Ratkaisu: Erilaisia kolmen pelivärin yhdistelmiä on vain kuusi erilaista. Nämä kaikki läpikäymällä (mikä näin pienen aineiston yhteydessä yleensä on riittävän yksinkertainen ratkaisutapa) oikea väriyhdistelmä löytyy helposti.

Toisaalta pelkkä järkeilykin vie perille. Selvästikään Hannun väri ei voi olla punainen, sillä jos olisi, myös Mikkoa koskeva väite olisi totta. Jos taas Mikko ei pelaa punaisilla, Tuomon olisi pakko pelata violeteilla, tai muuten häntä koskeva väittämä pitäisi paikkansa. Tällöin Hannu saisi punaiset, mikä olisi mahdotonta, koska myös näin tulisi kaksi totta väitettä. Siis on oltava niin, että Tuomo ei pelaa violeteilla on totta. Tällöin Mikko pelaa punaisilla ja Hannu ei, ja koska Tuomo ei pelaa violeteilla, on violetti Hannun ja vihreä Tuomon väri.

(Kyllä, tässä pulmassa esiintyneille henkilöille oikeine peliväreineen saattaa löytyä jonkinlaisia vastineita tosielämässä.)