kulmat

0

Nelikulmion lävistäjä

|

Opiskelijani Timo Hartikainen oli taannoin törmännyt Päivölän opistossa Suomen matemaattisen yhdistyksen olympiavalmennuksessa kiinnostavaan ongelmaan. Tehtävänanto kuuluu seuraavasti:

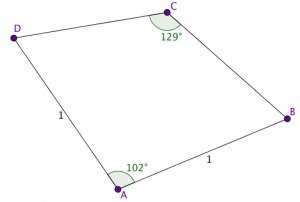
Nelikulmiossa ABCD kulma \angle A=102^{\circ}, kulma \angle C=129^{\circ} ja sivut |AD|=|AB|=1. Laske lävistäjän AC pituus.

Ratkaisu: Pulman ratkaisu perustuu jännenelikulmioon, eli nelikulmioon, jonka kärjet ovat ympyrän kehällä.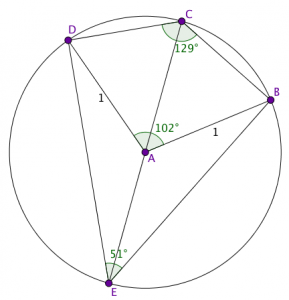 Nyt alkuperäinen nelikulmiomme ABCD ei ole jännenelikulmio, sillä jännenelikulmiossa vastakkaisten kulmien summa on aina 180^{\circ}. Sen sijaan jos täydennämme kuvaa niin, että mukaan tulee kärki E, jossa on 51^{\circ} kulma, tilanne muuttuu. Nyt koska 51^{\circ}=\frac{102^{\circ}}{2}, ja koska ympyrän keskuskulma on kaksinkertainen samaa kaarta vastaavaan kehäkulmaan verrattuna, on A keskipiste ympyrälle, jonka sisään piirretty jännenelikulmio EBCD on. Koska |AB|=|AD|=1, on myös AC=1, sillä sekin on ympyrän säde.

0

Kolmion kulma

|

Otetaanpa välillä yksi mielenkiintoinen perusgeometrian ongelma.colingeo

Oheisessa kuvassa piste P on ympyrän keskipiste ja pisteet A, B ja C ovat ympyrän kehän pisteitä. Piste D on suorien AP ja CB leikkauspiste ja janat PC ja CD ovat yhtä pitkät. Kulman \angle APB suuruus on 69^{\circ}. Kuinka suuri on kulma \alpha?

Ratkaisu: Kolmio PDC on tasakylkinen, joten myös kulma \angle CPD=\alpha. Koska kolmion yhden kulman vieruskulma on kolmion kahden muun kulman summa, saadaan \angle PCB=2\alpha. Koska myös PB on ympyrän säde, on kolmio PCB tasakylkinen, eli \angle PBC=2\alpha. Tästä edelleen vieruskulmalausetta soveltaen huomataan, että 2\alpha+2\alpha = \alpha + 69^{\circ}. Siis \alpha=23^{\circ}.

0

Tylppäkulmainen kolmio

|

Ajattelin aluksi kysyä seuraavaa. Valitaan tasosta kolme sattumanvaraista pistettä. Millä todennäköisyydellä ne ovat tylppäkulmaisen kolmion kärkipisteet?

Tämä pirullisen haastava pulma löytyy Charles Lutwidge Dodgsonin (eli Lewis Carrollin) kirjasta Pillow-Problems. Hän on siis keksinyt ja ratkonut pulman päässään unettomana yönä. Tähän ongelmaan liittyy kuitenkin isohko mutta: se ei ole hyvin määritelty, sillä riippuen ratkaisun lähestymistavasta tehtävään voi saada monta erilaista ratkaisua. Alkuperäisen ongelman täydellinen ratkaisu vaatisi noin seitsemän sivua hyvää matematiikkaa (sisältää juonipaljastuksia – älä avaa, jos haluat ratkoa pulman itse!), mikä ei suinkaan ollut alkuperäinen ajatukseni pulmaa tänne laittaessani. Kysytään siis nyt täsmällisemmin sitä, mitä halusin kysyä. Ihan riittävän vaikea tämä pulma on seuraavanlaisellakin muotoilulla.

Valitaan mielivaltaiset pisteet A ja B tasosta. Millä todennäköisyydellä kolmio ABC on tylppäkulmainen, kun AB on kolmion pisin sivu ja C on satunnainen tämän ehdon täyttävä piste?

Lisähupia ongelmaan saa sillä, että laskee todennäköisyyden tylppäkulmaiselle kolmiolle, kun AB on toiseksi pisin sivu.

Pulmaa muokattu 30.5.2016 klo 19.35 asiasta Facebookissa virinneen keskustelun vuoksi. Kiitokset avusta, Antti Saarinen ja Toni Vaahtera!