Tavarajuna ajaa pysähtymättä 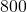kilometriä täsmälleen 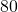kilometrin keskituntinopeudella. Sen nopeus ei kuitenkaan pysy matkan varrella vakiona. Osoita, että juna ajaa jonkin 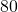kilometrin mittaisen pätkän matkastaan täsmälleen yhdessä tunnissa.

Tämä ongelma on jälleen Martin Gardneria parhaimmillaan, alkujaan Scientific American -lehden joulukuun 1979 numerosta.

Kuva: Henk Sijgers/Flickr (CC BY-NC 2.0)

Ratkaisu: Jaetaan matka-aika kymmeneen tunnin mittaiseen pätkään. Jos juna kulkee jonkin näistä aikana täsmälleen 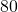kilometriä, on ongelma ratkaistu. Jos taas yhdessäkään näistä juna ei kulje täsmälleen 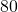kilometriä, valitaan kaksi peräkkäistä pätkää, joista toisen aikana matkataan hieman yli ja toisen aikana hieman alle 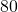kilometriä — kuinka päin, sillä ei ole väliä. Oletetaan yksinkertaisuuden vuoksi, että ensimmäisellä pätkällä keskinopeus oli jonkin verran alle 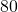km/h.

Kuvitellaan nyt, että meillä on tunnin mittainen aikajanatikku. Asetetaan se ensin ensimmäisen pätkän alkuun ja aletaan sitten liikuttaa sitä kohti jälkimmäisen pätkän loppua. Aikajanatikun osoittamana aikana kuljettu matka on aluksi alle 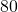kilometriä ja lopuksi yli 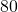kilometriä. Koska muutos on jatkuva, osuu johonkin kohtaan alku- ja loppupisteiden välille tasan tunnin mittainen pätkä, jonka aikana juna kulkee täsmälleen 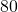kilometriä.

Pulmasta tekemäni Geogebra-appletti on saatavilla vapaasti Geogebratubessa. Ongelmaa vastaava kuvaaja on piirretty aika–matka-koordinaatistoon, jossa kunkin aikavälin keskinopeuden saa sekantin kulmakertoimena.