Kuva: Mark Seton/Flickr (CC BY-NC 2.0)
Tuomas ja Heikki pelaavat seuraavilla säännöillä kolikonheittopeliä. He heittävät (reilua, painottamatonta) kolikkoa, kunnes kolmella peräkkäisellä heitolla tulee joko heittosarja klaava-klaava-kruuna tai klaava-kruuna-kruuna. Tuomas voittaa ensimmäisessä ja Heikki jälkimmäisessä tapauksessa.
Millä todennäköisyydellä Tuomas voittaa pelin?
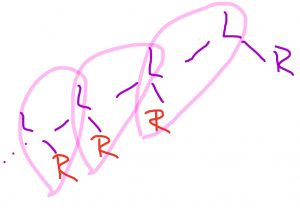
Kuva 1: Klaavaputki toimii Tuomaksen eduksi.
Ratkaisu: Tilannetta voidaan mallintaa monilla tavoilla. Tämäntyyppisissä ongelmissa tykkään itse yleensä lähteä piirtelemään tilannetta auki esimerkiksi puukaavion avulla. Merkitään kruunan heittämistä R:llä ja klaavan heittämistä L:llä. Koska kumpikin voittosarja alkaa klaavalla, voidaan olettaa, että ensimmäinen (relevantti) heitto on ollut klaava.
Jos toinenkin heitto on klaava, ollaan menossa kohti Tuomaksen voittoa (kuva 1). Nyt kruuna katkaisee pelin Tuomaksen eduksi, klaava jatkaa peliä, mutta pitää edelleen Tuomaksella ratkaisevan edun.
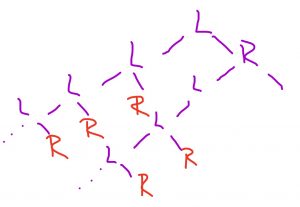
Kuva 2: Lisää Tuomaksen voittolinjoja.
Tuomaksen peli ei ole pelattu, vaikka seuraava heitto olisikin kruuna: yksi klaava lisää, ja tilanne palautuu olennaisesti samaksi kuin edellä (kuva 2).
Entäpä Heikin voittolinja tai voittolinjat? Mistä ne löytyvät? Heikki tarvitsee kaksi peräkkäistä kruunaa klaavan jälkeen. Jos saadan klaava, on Heikki aina kahden peräkkäisen onnistuneen heiton päässä voitosta. Tämä on ratkaiseva ero Tuomaksen hyväksi, sillä Tuomaksella voitto voi olla jo yhden heiton päässä. Kaikki sarjat, jossa kaksi klaavaa esiintyy peräkkäin johtavat lopulta Tuomaksen voittoon. Heikin voitto voi siis tulla vain seuraavilla heittosarjoilla: LRR, LRLRR, LRLRLRR, LRLRLRLRR jne. (kuva 3)
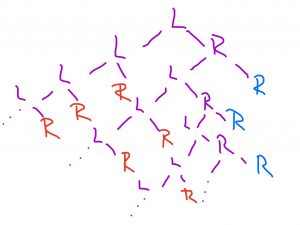
Kuva 3: Heikin voittolinjat.
Lasketaan nyt tarkalleen Heikin voittotodennäköisyys, josta Tuomaksen voittotodennäköisyys saadaan komplementtisääntöä käyttäen. Koska kolikko oli painottamaton, sekä kruunan että klaavan todennäköisyys on 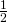 . Koska peräkkäiset heittokerrat ovat toisistaan riippumattomat, voidaan Heikin voittosarjat laskea kertolaskusääntöä soveltaen. Koska tarkastelu voitiin siis aloittaa ensimmäisestä klaavasta, on heittosarjan LRR todennäköisyys sama kuin kahden peräkkäisen kruunan, eli
. Koska peräkkäiset heittokerrat ovat toisistaan riippumattomat, voidaan Heikin voittosarjat laskea kertolaskusääntöä soveltaen. Koska tarkastelu voitiin siis aloittaa ensimmäisestä klaavasta, on heittosarjan LRR todennäköisyys sama kuin kahden peräkkäisen kruunan, eli 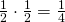 . Vastaavasti heittosarja LRLRR saadaan todennäköisyydellä
. Vastaavasti heittosarja LRLRR saadaan todennäköisyydellä 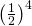 ja niin edelleen. Koska kaikki nämä heittosarjat ovat toisistaan riippumattomia, voidaan niiden yhteinen todennäköisyys laskea summana
ja niin edelleen. Koska kaikki nämä heittosarjat ovat toisistaan riippumattomia, voidaan niiden yhteinen todennäköisyys laskea summana
![Rendered by QuickLaTeX.com \[\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^4+\left(\frac{1}{2}\right)^6+\left(\frac{1}{2}\right)^8+\cdots .\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-c3a687d4d57dd0aba30f7baacfb91891_l3.png)
Tämä puolestaan on geometrinen sarja, jonka suhdeluku on 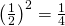 . Näin ollen Heikin voiton todennäköisyydeksi saadaan
. Näin ollen Heikin voiton todennäköisyydeksi saadaan
![Rendered by QuickLaTeX.com \[\frac{\frac{1}{4}}{1-\frac{1}{4}}=\frac{1}{3}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-7a24ad3fedff3b9c716349fd78da27e7_l3.png)
Komplementtisäännön nojalla Tuomas voittaa nyt todennäköisyydellä 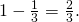
Tämä pulma löytyi Colin Beveridgen loistavalta Flying colors maths -sivustolta, jolla hän esittelee pulmaan ratkaisun parista muusta näkökulmasta. Colin on myös mainion huumorintajuinen heppu, jonka tekstejä on aina ilo lukea. Säännöllisehkön Twitter-yhteydenpitomme pohjalta Colin on lisännyt joihinkiin teksteihinsä Big in Finland -tunnisteen. Aika velikultia.
![]()
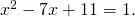 Tämän yhtälön ratkaisut ovat
Tämän yhtälön ratkaisut ovat 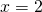 ja
ja 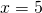 .
.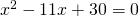 . Tämän ratkaisut ovat
. Tämän ratkaisut ovat 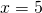 ja
ja 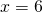 . Lisäehtona on, että kantaluvun
. Lisäehtona on, että kantaluvun 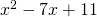 on poikettava nollasta. Kumpikin ratkaisuista totetuttaa tämän vaatimuksen.
on poikettava nollasta. Kumpikin ratkaisuista totetuttaa tämän vaatimuksen.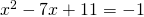 ja
ja 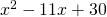 on parillinen. Nämä ehdot toteutuvat, kun
on parillinen. Nämä ehdot toteutuvat, kun 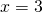 tai
tai 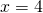 .
.![]() ,
, ![]() ,
, ![]() ,
, ![]() ja
ja ![]() .
.