Yleinen

5

Seepra

|

Seuraava pulma on kuuluisa 1960-luvun ongelma, jonka laatijaa ei varmasti tiedetä. On otaksuttu, että se olisi Albert Einsteinin käsialaa, mutta tämä on epätodennäköistä, sillä pulma ilmestyi ensi kerran vuonna 1962, kun Einstein kuoli jo 1955. Minä löysin sen Alex Bellosilta, mutta tuntuu, että olen törmännyt siihen aiemminkin. Tässä se tulee, pirullisen kiehtova pulma. Ja kyllä – informaatiota on riittävästi, vaikka alkuun siltä ei tunnukaan. Kynä ja paperia esille!

  1. Kadulla on viisi taloa.
  2. Punaisessa talossa asuu skotti.
  3. Kreikkalaisella on koira.
  4. Vihreässä talossa juodaan kahvia.
  5. Bolivialainen juo teetä.
  6. Vihreä talo on harmaan talon oikeanpuoleinen naapuri.
  7. Farkkujen käyttäjällä on etanoita.
  8. Keltaisen talon omistaja käyttää haaremihousuja.
  9. Keskimmäisessä talossa juodaan maitoa.
  10. Tanskalainen asuu ensimmisessä talossa.
  11. Shortsien käyttäjä asuu ketun omistajan naapurissa.
  12. Haaremihousuja käytetään hevosen talon naapurissa.
  13. Trikoiden käyttäjä juo appelsiinimehua.
  14. Japanilaisella on pellavahousut.
  15. Tanskalainen asuu sinisen talon vieressä.

Viikon vaikea pulma on kaksiosainen. Kuka juo vettä? Entä kenen lemmikki on seepra? (Selvennys: joka talossa on asukas eri maista, kaikkialla juodaan eri juomaa ja kaikilla on eri lemmikki ja erilaiset housut.)

Kuva: Bryan Jones / Flickr (CC BY-NC-ND 2.0)

1

Synttärit!

|

imageOpettaja H:n pulmakulma täytti äskettäin vuoden. Hups! Tässä ajassa se on oppinut kosolti uusia temppuja, syömään kiltisti paikallaan, konttaamaan eteen ja taakse sekä julkaisemaan tasaisen epätasaisen tasoisia pulmia kaikkien pähkäiltäväksi. Minulla pulmakulman ylläpidossa on ollut hauska ja opettavainen vuosi – toivottavasti muutkin olette viihtyneet, niin satunnaiset seikkailijat kuin (molemmat) kanta-asiakkaatkin!

Viikon helppona pulmana on antaa palautetta vaikkapa tämän postin kommenttikenttään, niin ruusuja kuin risujakin. Samalla, jos haluatte, voitte myös nimetä jonkin suosikkipulmanne vuoden varrelta.

Pähkäilemisiin!

–Opettaja H.

0

Pennirinki

|

Seuraava pulma on Charles Lutwidge Dodgsonin alias Lewis Carrollin kirjasta Pillow-Problems vuodelta 1895. Kirjassa on 72 ongelmaa, jotka Dodgson kertoo kehitelleensä ja ratkoneensa päässänsä unettomina öinä. Kirjan ongelmien vaikeustaso vaihtelee hurjasta helpohkoihin, ehkäpä yläpäätä painottaen. Tämä ongelma on sieltä kevyemmästä päästä.

Viisi roistoa istuu ringissä ja jokaisella miehellä on yhtä monta penniä. Älykkäin heistä ehdottaa pientä pennipeliä. Ensinnäkin kaikki saavat numeron, älykkäin ykkösen, seuraava kakkosen, sitten kolmonen, nelonen ja vielä vitonen. Nyt älykkäin laittaa kaikki penninsä pussiin, antaa sen kolmoselle, jonka pitää ensin ottaa kummallekin naapurilleen pussista naapurin numeron osoittama määrä pennejä. Sitten kolmosen pitää laittaa pussiin puolet siitä määrästä pennejä, joka pussissa oli sen saapuessa hänelle. Sitten kolmonen antaa pussin vitoselle, joka antaa myös pussista pennit vierustovereille, lisää puolet siitä summasta, joka pussissa oli sen tullessa hänelle, ja antaa pussin kaksi paikkaa eteenpäin. Jos sattuisi käymään niin, että rahanlisäysvaiheessa itsellä ei olisi tarpeeksi rahaa pussin täydentämiseen, saisi kenen tahansa muun paitsi numero ykkösen pennipinosta täydentää puuttuvan määrän.

Kun pussi tulee takaisin ykköselle, hän nakkaa kaksi saamaansa rahaa pussiin, vetää pussin nyörit kiinni ja pakenee vauhdilla paikalta. Muut neljä roistoa jäävät hölmistyineinä katsomaan tyhjin käsin – ryökäle nappasi kaikki rahat! Kuinka monta penniä kullakin roistolla oli aluksi?

Ratkaisu: Olkoon kullakin konnalla aluksi k kolikkoa. Peli etenee seuraavasti:

  1. Numero 3 sai pussin jossa on k kolikkoa ja hän antoi pois 2+4=6 kolikkoa. Sitten hän laittaa pussiin \frac{k}{2} kolikkoa, joten pussiin jää k+\frac{k}{2}-6=\frac{3}{2}k-6 kolikkoa.
  2. Numero 5 jakaa pois 4+1=5 kolikkoa ja puolitoistakertaistaa pussissa olleen rahasumman. Loppusumma hänen vuoronsa jälkeen on siis \frac{3}{2}\left(\frac{3}{2}k-6\right)-5.
  3. Numero 2 jakaa pois 1+3=4 kolikkoa ja puolitoistakertaistaa pussin summan. Pussin rahamäärä on hänen jälkeensä \frac{3}{2}\left(\frac{3}{2}\left(\frac{3}{2}k-6\right)-5\right)-4.
  4. Numero 4 jakaa pois 3+5=8 kolikkoa ja puolitoistakertaistaa pussin summan. Pussin rahamäärä on hänen jälkeensä \frac{3}{2}\left(\frac{3}{2}\left(\frac{3}{2}\left(\frac{3}{2}k-6\right)-5\right)-4\right)-8.
  5. Numero 1 lisää pussiin kaksi kolikkoa, jonka jälkeen pussissa on 5k kolikkoa.

Tästä saadaan yhtälö 

    \[\frac{3}{2}\left(\frac{3}{2}\left(\frac{3}{2}\left(\frac{3}{2}k-6\right)-5\right)-4\right)-8+2=5k,\]

jonka ratkaisu on k=696.

Sivumennen sanoen: olisi ehkä jäänyt ratkaisematta ilman kynän ja paperin apua. Eli onnea vain Lewis Carrollille, jos päässään yöllä tämän pyöritteli loppuun asti.

0

Pojat pimeässä

|

Kössi, Johannes, Tuomas ja Mikko ovat pimeässä metsässä kapean polun päässä. Heidän pitäisi ehtiä 16 minuutin päästä lähtevään linja-autoon, mutta polun vaarojen ja monttujen vuoksi he tarvitsevat lampun. Heillä on vain yksi lamppu, eikä valo riitä kerrallaan kuin kahdelle pojalle turvalliseen kulkuun. Nopsajalkainen Kössi tarvitsee polun kulkemiseen vain minuutin, ponteva Johannes kaksi minuuttia, jalkaansa rakon saanut Tuomas viisi minuuttia ja nilkkansa nyrjäyttänyt Mikko kahdeksan minuuttia. Voivatko pojat ehtiä bussiin?

Kuva: Jon Bunting/Flickr (CC BY 2.0)

Kuva: Jon Bunting/Flickr (CC BY 2.0)

Ratkaisu: Pojat ehtivät bussiin seuraavasti:

  • Kössi ja Johannes menevät ensin. (2 minuuttia)
  • Kössi palaa takaisin tuoden lampun Mikolle ja Tuomaalle. (1 minuutti)
  • Tuomas ja Mikko menevät pysäkille. (8 minuuttia)
  • Johannes palaa takaisin. (2 minuuttia)
  • Johannes ja Kössi palaavat pysäkille. (2 minuuttia)

Yhteensä aikaa kuluu siis 15 minuuttia, joten heillä on aluksi vieläpä minuutti aikaa ratkaista tämä pulma.

 

0

Tangenttikolmio

|

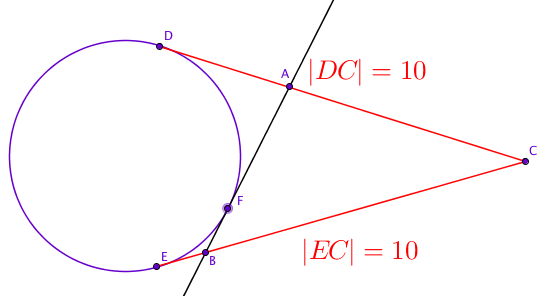Näyttökuva 2015-12-11 kello 15.46.15Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä C. Tangenttien sivuamispisteet D ja E ovat etäisyydellä 10 pisteestä C. Piirretään ympyrälle vielä yksi tangentti pisteiden C ja D välisellä kaarella olevan pisteen F kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet A ja B. Laske kolmion ABC piiri.

Martin Gardner ainakin on tätä ongelmaa esitellyt.

Ratkaisu: Aivan vastaavasti kuin piste C on tangenttikulman kärki, myös pisteet A ja B ovat. Voidaan helposti osoittaa, että tangenttikulman kärki on aina yhtä etäällä molemmista tangenttipisteistä, eli samaan tapaan kuin |DC|=|EC|, voidaan myös todeta, että |AD|=|AF| ja |BE|=|BF|. Siis kolmion ABC piiri on 20.

0

49 jakajana

|

Ensin huomataan, että

    \[\frac{\frac{1}{50}}{1-\frac{1}{50}}=\frac{\frac{1}{50}}{\frac{49}{50}}=\frac{1}{49}.\]

Siis geometriseksi sarjaksi kehiteltynä

    \[\frac{1}{49}=\frac{1}{50}+\left(\frac{1}{50}\right)^2+\left(\frac{1}{50}\right)^3+\left(\frac{1}{50}\right)^4+\ldots .\]

Jos näin muodostuvaa desimaalilukua käsitellään kahden desimaalin palasina, ovat jälkimmäiset kaksi aina yhden viideskymmenesosan eli kaksi sadasosaa edellisistä. Käytännön laskutoimituksissa tämä johtaa yllättävän helppoon desimaalikehitelmän muodostamiseen. Toimi seuraavasti:

  1. Kerro osoittaja kahdella. Kaksi ensimmäistä desimaalia on tässä. Jos tulos on vähintään 50, lisää siihen 1. Jos tulos on vähintään sata, jätä ykkönen alusta pois. Jos tulos on alle 10, lisää nolla eteen.
  2. Kerro edelliset kaksi desimaalia kahdella. Jos tulos on vähintään 50, lisää siihen 1. Jos tulos on vähintään sata, jätä ykkönen alusta pois. Jos tulos on alle 10, lisää nolla eteen.
  3. Ja niin edelleen.

Tämä algoritmi todella toimii! Ja jossain vaiheessa se jaksokin tulee kyllä vastaan – pakkohan sen on, koska kyseessä on ilmeinen rationaaliluku. (Jakson pituus tässä tapauksessa on muuten korkeintaan 42 numeroa.)

Otetaan esimerkiksi luku \frac{18}{49}. Kerrotaan ensin osoittaja kahdella: 2\cdot 18=36. Luvun alku on siis 0,36. Edelleen 36\cdot 2 =72, mutta koska 72\geq 50, lisätään 1. Alku on siis 0,3673. Nyt 73\cdot 2=146, joten tästä jätetään ykkönen alusta pois. Olemme saaneet 0,367346. Ja kun tästä jatkamme, saamme

    \[\frac{18}{49}=0,367346938775510204081632\ldots.\]

Kokeile nyt itse! Muodosta desimaalikehitelmät luvuille \frac{11}{49}, \frac{41}{49} ja \frac{8}{49}.

Jos lukuja jaetaan 7:llä, liittyy näin muodostuviin desimaalikehitelmiin eräs hauska ominaisuus. Muodosta desimaalikehitelmät luvuille \frac{1}{7}, \frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7} ja \frac{6}{7}. Huomaatko? Käytä apuna taitoasi 49:llä jakamisessa.

Vastaava temppu yleistyy myös 499:llä, 4999:llä, 49999:llä jne. jakamiseen. Pienellä vaivalla sovellusalueita löytyy lisääkin.

Opin tämän tempun Colin Beveridgeltä. Lähdeteksti löytyy osoitteesta http://www.flyingcoloursmaths.co.uk/mathematical-ninja-divides-49/.

0

Julkisivuremontti

|

Pulmablogi hakee vähän toimivampaa ulkoasua. Olen joutunut ongelmiin erityisesti matemaattisen typografian, eli \LaTeX-koodauksen kanssa, enkä oikein meinaa löytää hyvää ratkaisua tähän. Tästä syystä lähiaikoina sivuilla nähtäneen monenlaisia kokeiluja sekä huonommin ja paremmin luettavaa matematiikkaa. Joka tapauksessa on selvää, että sivuston ulkoasu muuttuu sangen erilaiseksi, sillä nykyinen sivuteema ei taida tarpeisiini sittenkään kunnolla taipua. Kärsivällisyyttä, ystävät, kyllä tämä tästä ehkä.

0

Uusi pulmablogi!

|

 

Heipä hei!

Tervetuloa Opettaja H:n pulmakulmaan, suomenkieliseen ongelmamatematiikkaan keskittyvään blogiin. Tarkoituksenani on julkaista parin ongelman viikkovauhdilla erinäisistä lähteistä löytämiäni kiinnostavia pulmia. Pyrin tarjoamaan monipuolisia ja monentasoisia pähkinöitä pikku vitseistä huippuhankaliin mallinnustehtäviin. Laadin kaikkiin ongelmiin myös ratkaisut, mutta en tietenkään ihan heti!

Mukavia hetkiä ajanvietematematiikan parissa!