Ratkaisut

0

Lisää tyttöjä – ratkaisu

|

Eräässä teoreettisessa valtiossa haluttiin, että naisten osuus väestöstä kasvaisi. Niinpä valtion parlamentti hyväksyi lain, jonka mukaan kuhunkin perheeseen piti saada tyttölapsi. Jos perheeseen oli syntynyt tyttö, oli lasten hankkiminen lopetettava. Jos taas perheessä oli vain poikalapsia, oli lasten hankkimista jatkettava tytön syntymiseen asti. Oletetaan, että jokainen syntyvä lapsi on joko tyttö tai poika. Oletetaan myös, että tyttöjen ja poikien syntymätodennäköisyydet ovat samat. Kun populaation koko vähitellen tasoittuu, kuinka suureksi tyttöjen osuus syntyvistä lapsista kasvaa? Jatko-ongelmana voidaan pohtia, mikä on suurin mahdollinen tyttöjen osuus populaatiosta ja millä (riittävän humaaneilla) keinoilla se voidaan saavuttaa.

Ongelman ratkaisu on hyvin yksinkertainen, ja samalla saadaan vastaus myös jatko-ongelmaan. Jos nimittäin tyttöjen ja poikien syntymätodennäköisyydet ovat kuitenkin samat, on lapsista puolet tyttöjä ja puolet poikia, eikä suhde millään peukaloinnilla siitä muutu.

Asia voidaan järkeillä vielä vaikka seuraavasti. Perheiden ensimmäisistä lapsista puolet on tyttöjä, puolet poikia. Perheiden toisista lapsista puolet on tyttöjä ja puolet poikia. Perheiden kolmansista lapsista puolet on tyttöjä, puolet poikia. Ja niin edelleen. Puolet ja puolet.

0

Juokseva koira – ratkaisu

|

Koira lähtee juoksemaan vakionopeudella 50 metriä pitkän jonon perältä kohti jonon kärkeä. Jono lähtee samaan aikaan liikkeelle, myös vakionopeudella. Kun koira saavuttaa jonon kärjen, se kääntyy välittömästi takaisin (oletetaan siis, että tähän ei kulu aikaa) ja jatkaa matkaansa samalla vakionopeudella kohti jonon häntää. Kun koira saavuttaa jonon hännän, on jono edennyt 50 metriä. Kuinka pitkän matkan koira juoksi?

Juoksevan koiran ongelman ratkaiseminen vaatii hieman yksinkertaista ymmärrystä fysiikasta (mikä kuvaa täsmälleen omaa tasoani) sekä lievää luovuutta käytettävien yksiköiden kanssa. Päärooli on nopeuden, matkan ja ajan välisellä perusyhteydellä v=\frac{s}{t}, josta saadaan, että aika t voidaan ilmaista t=\frac{s}{v}.

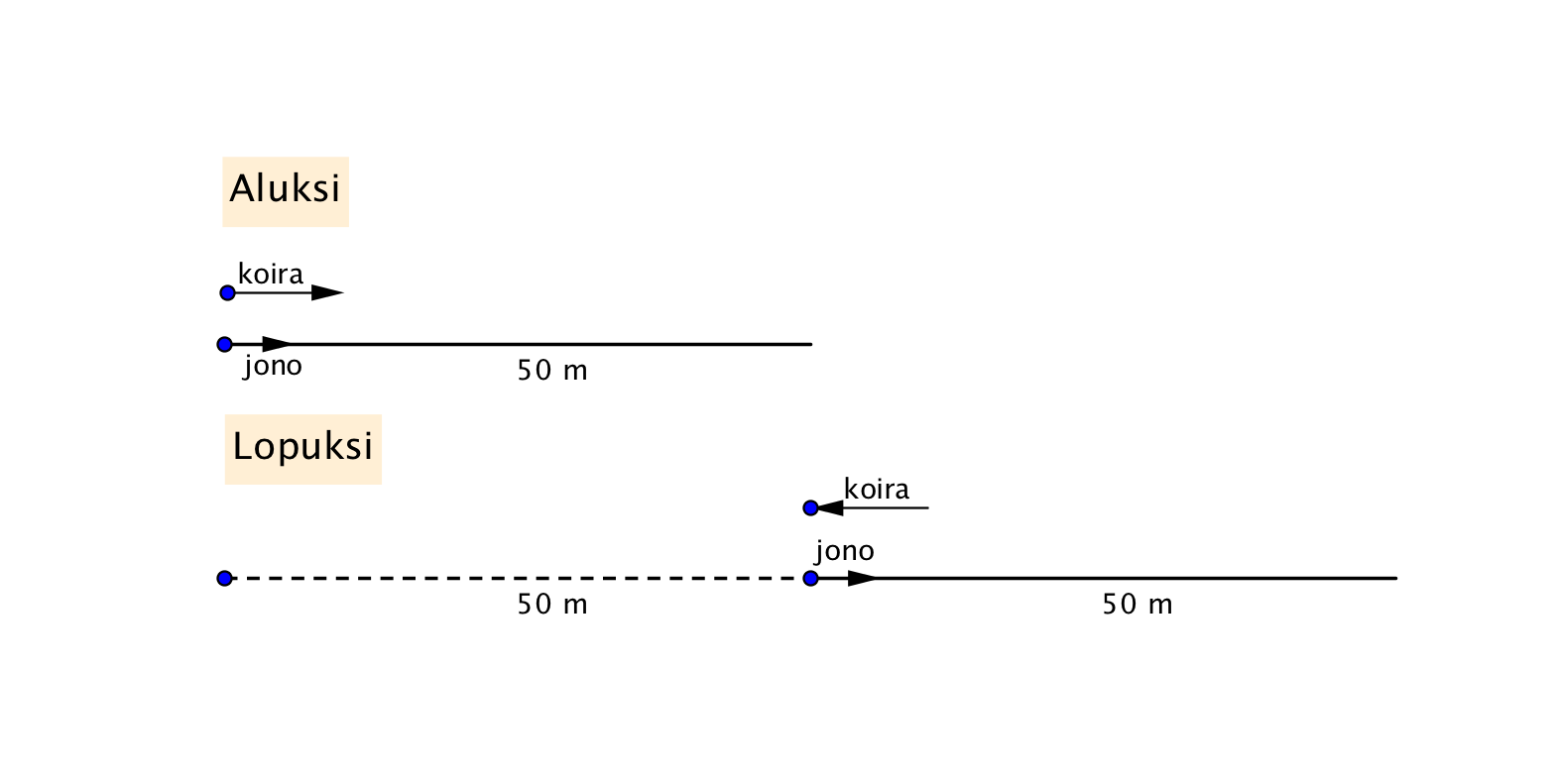Aletaan ensin muokata käytettäviä yksiköitä meille sopiviksi. Olkoon 50 metriä 1 ”matka” ja olkoon ajan t yksikkönä ”aika, joka jonolta kuluu 1 matkan kulkemiseen”. Tällöin jonon nopeutta voidaan merkitä 1:llä.koiranratkaisuTutkitaan sitten koiran juoksemiseen kuluvaa aikaa. Jaetaan aika kahteen osaan, jonon kärjen saavuttamiseen t_1 ja jonon hännille palaamiseen t_2. Nyt siis t_1 on aika, jossa koira juoksee 50 metriä (eli yhden ”matkan”) jonoa enemmän. Merkitään koiran nopeutta  x, jolloin sen nopeus suhteessa jonoon on x-1. Näin ollen t_1=\frac{1}{x-1}. Vastaavasti paluumatkalla koiran nopeus suhteessa jonoon on x+1, joten t_2=\frac{1}{x+1}. Koska t_1+t_2=1, saadaan yhtälö, joka ratkaisee ongelman:  \frac{1}{x-1}+\frac{1}{x+1}=1.

Yhtälö saadaan muokattua muotoon x^2-2x-1=0. Tämän yhtälön juurista x=1\pm\sqrt{2} vain positiivinen vaihtoehto x=1+\sqrt{2} hyväksytään. Koiran nopeus on siis  (1+\sqrt{2}) 50 metrin matkaa ajassa, joka jonolta 50 metriin kuluu, joten ongelman vastaus on  (1+\sqrt{2})\cdot 50=120,71\ldots\approx 121 metriä.

Juoksevan koiran ongelma johtaa toiseen, hieman haastavampaan pulmaan: mitäpä, jos koira juoksisikin neliön muotoisen marssimuodostelman ympäri? Jos neliön sivu olisi 50 metriä ja muodostelma etenisi 50 metriä, kuinka pitkän matkan koira juoksisi? Ratkaisussa tarvittava yhtälö on vain hieman monimutkaisempi kuin tässä esitelty. Kokeilepa ratkaista, ja kerro tuloksistasi vaikkapa tämän blogin kommenttiosioon!

0

Neliön ja ympyrän piiri – ratkaisu

|

Neliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä. Kummalla on suurempi piiri, neliöllä vai ympyrällä?

Tähän ongelmaan on olemassa monta hieman erilaista ratkaisutapaa. Muiden muassa Pythagoraan lauseen, kehäkulmien ja keskuskulmien sekä trigonometrian peruskaavan kautta vastaus voidaan päätellä. Tässä esittelemäni ratkaisulinja nojaa puolestaan yhdenmuotoisiin kolmioihin, ja koska siihen liittyy eräs elegantti tulos, on se mielestäni erityisen kiinnostava. Alun perin tämä ongelma ratkaisuineen tuli vastaan Colin Beveridgen blogissa.

Täydennettään alkuperäistä kuvaa hieman. 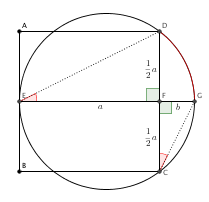Piirretään ympyrälle halkaisija EG, joka leikkaa neliön sivua CD pisteessä F. Merkitään neliön sivun pituudeksi a ja janan FG pituutta b. Yhdenmuotoisissa kolmioissahan vastinosien pituuksien suhde säilyy. Kolmioiden yhdenmuotoisuuden osoittamiseksi riittää näyttää, että kolmioissa on kaksi yhtä suurta vastinkulmaparia. Kuvan kolmiot FED ja FCG ovat yhdenmuotoiset, sillä kulma F on molemmissa suora ja lisäksi molemmista kolmioista löytyy samaa kaarta DG vastaavat kehäkulmat, jotka kehäkulmalauseen mukaan ovat yhtä suuret.

Nyt, koska vastinsivujen suhde säilyy, saadaan yhtälö \frac{EF}{FD}=\frac{CF}{FG}, eli \frac{a}{\frac{1}{2}a}=\frac{\frac{1}{2}a}{b}, josta b=\frac{1}{4}a, eli ympyrän halkaisija on \frac{5}{4}-kertainen neliön sivuun verrattuna. Tästä seuraa se, että ympyrän piiri on \frac{5\pi}{4}a, joka on hieman vähemmän kuin neliön piiri 4a.

Minun mielestäni ratkaisun hienous perustuu juuri tähän yhdenmuotoisten kolmioiden käyttöön, sillä se tekee ratkaisusta hyvin lyhyen ja suoraviivaisen. Itse asiassa tässä hyödynnetään kaikille jännenelikulmioille yhteistä ominaisuutta: lävistäjien leikkauspiste jakaa lävistäjät siten, että leikkautuvien osien tulo on vakio. Tämä tulos saadaan välittömästi yhdenmuotoisista kolmioista, olipa jännenelikulmio millainen tahansa. Tulosta voi kokeilla oheisella Geogebra-appletilla pisteitä liikuttelemalla.

2

Tiukka tennisottelu – ratkaisu

|

Tennisottelu kestää täydet viisi erää. Toisen pelaajan erissä voittamat pelit muodostavat aritmeettisen jonon. Kumpi voitti ottelun, kun kumpikin pelaajista voitti yhtä monta peliä?

Aritmeettisella jonolla tarkoitetaan lukujonoa, jossa peräkkäisten termien erotus on vakio. Siis esimerkiksi parilliset positiiviset kokonaisluvut muodostavat aritmeettisen jonon (2,4,6,\ldots), mutta kakkosen potenssit (1,2,4,8,\ldots) eivät.

Tennisottelussa erän voittamiseen tarvitaan yleensä 6, joskus 7 ja ainoastaan viidennen erän ollessa kyseessä mahdollisesti enemmän kuin 7 voitettua peliä. Siispä mikäli ”aritmeettinen” pelaaja voittaisi ottelun, olisi hänen voitettava erissä 6, 7 ja 8 peliä. Näin ollen hänen erissä voittamiensa pelien jono olisi välttämättä 4, 5, 6, 7, 8. Näin ollen voidaan pitää varmana, että erien tulokset ovat 4–6, 5–7, 6–X, 7–Y ja 8–6, missä 0\leq X\leq 4 ja Y=5 tai Y=6. Näissä tapauksissa aritmeettinen pelaaja voittaisi 30 peliä ja vastapelaaja 19+X+Y peliä, mikä selvästi on mahdotonta. Siis aritmeettinen pelaaja ei voi voittaa.

Minkälaisin pistein aritmeettinen pelaaja sitten voi hävitä ottelun? Voittaakseen kaksi erää neljästä ensimmäisestä hänen on saavutettava niissä 6 ja 7 voitettua peliä. Kävisikö 7, 6, 5, 4, 3? Tällöin ottelun tulos voisi olla A–7, B–6, 7–5, 6–4, 6–3. Koska aritmeettinen pelaaja voittaisi tässä mallissa 25 peliä ja koska A=5 tai A=6, voi B olla vastaavasti joko 1 tai 0. Mahdollisia ratkaisuja ovat siis ainakin 5–7, 1–6, 7–5, 6–4, 6–3 ja 6–7, 0–6, 7–5, 6–4, 6–3. Toisinpäin tämä tulosjono ei toimi – aritmeettinen ei siis voi ensin alkaa hävitä eriä.

Vai voiko sittenkin? Itse asiassa voi, mutta tällöin tarvitaan aritmeettinen jono 4, 5, 6, 7, 8. Tämä johtaa loppupisteisiin 6–4, 7–5, 1–6, 6–7, 10–8 tai 6–4, 7–5, 2–6, 5–7, 10–8. Erikoistapauksena siis viidennessä erässä ei pelata tie-breakia, joten sen erän voi hävitä myös 8 peliä voitettuaan.

Jos otetaan lukuun erikoistapaus, jossa vakiojono lasketaan aritmeettiseksi, saadaan vielä seuraavankaltainen tulossarja: 4–6, 4–6, 7–6, 7–6, 8–6. Tässä neljän ensimmäisen erän tulokset ovat järjestettävissä mihin tahansa järjestykseen, joten kaikkiaan tennisotteluongelmaan on 10 ratkaisua – joissa kaikissa voittajaksi selviytyy ei-aritmeettinen pelaaja. Tennistä pelatessaan kannattaa siis jättää lukujonot syrjään ja treenata esimerkiksi ykkössyöttö kuntoon!