Viikon vaikea

2

Venäläisen talonpojan kertolasku

|

Satun tykkäämään kovasti päässälaskusta ja erilaisista siihen liittyvistä tempuista. Mielestäni sopivan isojen lukujen kertolasku päässä on mainio tapa vaivata hoksottimiaan. Lisäksi päässälasku avaa tehokkaasti erilaisia yhteyksiä lukujen välillä ja kaiken kaikkiaan laajentaa matemaattisen ymmärryksen ja osaamisen skaalaa. Ja hei, jos jokin asia on yksinkertaisesti hauskaa, miksipä sitä ei harrastaisi!

Nyt päässälaskusta on tulossa hyvin ajankohtainen asia myös lukiossa, sillä Ylioppilastutkintolautakunta on keväästä 2016 alkaen uudistamassa sekä lyhyen että pitkän matematiikan koetta. Jatkossa kokeen neljään ensimmäiseen tehtävään vastataan ilman laskimia – avaus, joka ainakin oman kouluni kollegojen keskuudessa on otettu ehdottomasti oikeana ilolla vastaan. Meidän kokeissamme päässälaskuosio on ollut varsinkin alkupään kursseilla mukana jo muutamia vuosia. Odotan kiinnostuneena, kuinka tymäkkää matematiikkaa YTL abiturienteille neljään ensimmäiseen tehtävään tarjoilee.

Mutta asiaan. Selailin tovi sitten Theoni Pappasin hienoa opusta Lisää matematiikan iloja (Terra Cognita 2001), kun silmiini sattui mielenkiintoinen tapa laskea hieman helpotetusti suurehkojen lukujen tuloja – jos ei nyt ihan puhtaana päässälaskuna, niin sutjakasti kynällä ja paperilla kuitenkin. Pappasin mukaan kyseistä menetelmää kutsutaan venäläisen talonpojan kertolaskuksi.

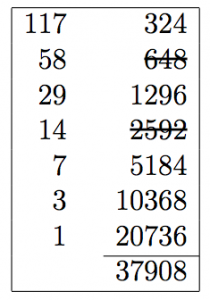Näyttökuva 2015-8-29 kello 20.37.00Otetaan esimerkiksi vaikkapa tulo 117\cdot 324. Homma toimii seuraavasti: jaetaan toista luvuista toistuvasti kakkosella. Jakojäännöksestä ei tarvitse välittää, vain kokonaiset lasketaan. Näin edetään, kunnes ollaan päästy ykköseen. Viereiseen sarakkeeseen aletaan puolestaan kertoa toista luvuista toistuvasti kakkosella. Kun ollaan päästy yhtä pitkälle kuin vasemmalla, vedetään yli kaikki ne luvut, jotka vastaavat parillista lukua vasemmanpuoleisessa sarakkeessa. Jäljelle jäävät luvut lasketaan yhteen, ja halutun tulon arvo on saatu.

Kysymys kuuluukin, että miksi tämä menetelmä toimii mille tahansa kokonaislukujen tulolle. Ratkaisu on tässä.

0

Kaksi jokilaivaa

|
IMLS Digital Collections & Content / Flickr (CC BY 2.0)

IMLS Digital Collections & Content / Flickr (CC BY 2.0)

Kaksi jokilaivaa lähtee samaan aikaan joen vastakkaisilta rannoilta tasaisella nopeudella suoraviivaisesti kohti vastarantaa; toinen laivoista on nopeampi. Kun laivat kohtaavat, on lähempi ranta 720 metrin päässä. Molemmat laivat pysähtyvät rannalle kymmeneksi minuutiksi, ja kun ne kohtaavat seuraavan kerran, ovat ne 400 metrin päässä toisesta rannasta. Kuinka leveä joki on?

Martin Gardnerin ongelma, tietenkin. Ratkaisu löytyy tästä. Ensi viikolle keksin sitten jotain ihan muuta.

0

Kuution sahaus

|

Rubikin kuutio voidaan jakaa kuudella suoralla sahauksella 27 tasakokoiseksi pieneksi kuutioksi kuvan osoittamalla tavalla. Jos yksittäisen sahauksen jälkeen kuution osia voisi mielensä mukaan järjestellä uudelleen, olisiko mahdollista vähentää tarvittavien sahauksien määrää?

Tämäkin ongelma kumartaa kauniisti Martin Gardnerin suuntaan. Ratkaisu löytyy tästä.rubiks-cube-145949_640

4

Kuinka monta rationaalilukua on?

|

Montako on paljon? Kumpi joukoista on suurempi? Kysymys on yksinkertainen siihen asti, kun kaikki joukon alkiot voidaan luetella. Se joukko, jossa on enemmän alkioita, on suurempi. Niin kauan kuin tarkastelemme joukkoja, joissa on sata tai miljardi tai vaikka 10^{4023}  alkiota, on käsiteltäviä alkioita vain äärellinen, laskettavissa oleva määrä, joka voidaan ilmoittaa luonnollisella luvulla.

Asiat muuttuvat, kun alkioita onkin äärettömästi. Äärettömyys on äärettömän kiehtova teema matematiikassa (ja matematiikan opettajien ilmeiset vitsit ovat äärettömän kehnoja). Äärettömyyksiä on eri kokoisia. Numeroituvasti ääretön joukko on sellainen, jonka alkiot voitaisiin luetella jossakin järjestyksessä, mikäli aikaa olisi loputtomiin käytettävissä. Esimerkiksi luonnollisten lukujen joukko \mathbb{N}=\{0,1,2,3,4,\ldots\} on numeroituvasti ääretön, kuten myös vaikkapa parillisten luonnollisten lukujen joukko \{0,2,4,6,\ldots\}. Numeroituvasti äärettömillä joukoilla sanotaan olevan sama kardinaaliluku, mikä tarkoittaa, että (sikäli kuin joukkojen alkioden lukumäärästä voidaan mielekkäästi puhua) joukoissa on yhtä monta alkiota.

Toki näyttää siltä, että luonnollisia lukuja on tuplasti enemmän kuin parillisia luonnollisia lukuja, mutta itse asiassa onkin niin, että niitä on ”yhtä äärettömästi”. Mikä olisi kätevä tapa osoittaa tämä?

Rationaaliluvut ovat tiheitä reaalilukujen joukossa, eli kun valitaan mitkä tahansa kaksi reaalilukua, niin niiden väliin mahtuu aina rationaaliluku. Tämä ominaisuus ei selvästikään ole esimerkiksi luonnollisilla luvuilla voimassa. Mutta voitaisiinko silti osoittaa, että rationaalilukuja on ”yhtä äärettömästi” kuin luonnollisia lukuja?

0

Lisää tyttöjä

|

Eräässä teoreettisessa valtiossa haluttiin, että naisten osuus väestöstä kasvaisi. Niinpä valtion parlamentti hyväksyi lain, jonka mukaan kuhunkin perheeseen piti saada tyttölapsi. Jos perheeseen oli syntynyt tyttö, oli lasten hankkiminen lopetettava. Jos taas perheessä oli vain poikalapsia, oli lasten hankkimista jatkettava tytön syntymiseen asti. Toisin sanoen perheiden oli hankittava lapsia tytön syntymiseen asti.

Oletetaan, että jokainen syntyvä lapsi on joko tyttö tai poika. Oletetaan myös, että tyttöjen ja poikien syntymätodennäköisyydet ovat samat. Kun populaation koko vähitellen tasoittuu, kuinka suureksi tyttöjen osuus syntyvistä lapsista kasvaa? Jatko-ongelmana voidaan pohtia, mikä on suurin mahdollinen tyttöjen osuus populaatiosta ja millä (riittävän humaaneilla) keinoilla se voidaan saavuttaa.

Tämä pulma kuuluu tilastomatematiikan klassikkoihin. Viimeisimpänä sen tapasin The Guardianiin pähkinäpalstaa kirjoittavan Alex Bellosin videoblogista. Bellos on kirjoittanut kirjoja paitsi matematiikasta myös jalkapallosta, joten hän on sikälikin sangen fiksu heppu.

Ongelman ratkaisu on tässä.

2

Neliön ja ympyrän piiri

|

nelio_ja_ympyraNeliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä. Kummalla on suurempi piiri, neliöllä vai ympyrällä?

Tämä ongelma on mielestäni yllättävän haastava – paljon vaikeampi kuin miltä se äkkiseltään näyttää – mutta se on kyllä ratkaistavissa lukion pitkän matematiikan taidoilla. Lisäksi ratkaisu pitää sisällään hauskan yleispätevän lisätuloksen, jota harvoin tulee ajatelleeksi.

Ratkaisu ongelmaan on tässä.

0

Juokseva koira

|

Pulmakulmani ensimmäinen ongelma on vanha Martin Gardnerin klassikko. Kuulin ongelman ensimmäisen kerran opetusharjoitteluni aikana eräältä lyhyen matematiikan opiskelijalta. Tässä onkin vinkki sen ratkaisemiseen: hirveän monimutkainen mallinnus ei ole tarpeen! Oli hauskaa katsoa, kun viisi yliopistotason fyysikkoa piirtelee taulun täyteen yhtälöitä parin päivän ajaksi ja takoo päätään seinään. Lopulta sangen yksinkertainen ja yleispätevä malli vie maaliin asti. Mutta asiaan.

Koira lähtee juoksemaan vakionopeudella 50 metriä pitkän jonon perältä kohti jonon kärkeä. Jono lähtee samaan aikaan liikkeelle, myös vakionopeudella. Kun koira saavuttaa jonon kärjen, se kääntyy välittömästi takaisin (oletetaan siis, että tähän ei kulu aikaa) ja jatkaa matkaansa samalla vakionopeudella kohti jonon häntää. Kun koira saavuttaa jonon hännän, on jono edennyt 50 metriä. Kuinka pitkän matkan koira juoksi?

Ongelman ratkaisu on tässä.