Viikon vaikea

2

Paiholalainen pankkineuvoja

|

Tämä on hieman erilainen ongelma kuin oikeastaan kaikki muut tässä blogissa aiemmin esitellyt pulmat. Nyt nimittäin siirrytään matematiikkaa hieman vähemmän eksaktin tieteen eli pörssikeinottelun pariin. Ja koska tiede ei ole ihan niin eksaktia, myöskään ongelman muotoilu (ja sitä myöden myöskään sen ratkaisu) eivät välttämättä ole ihan tarkkoja. Mutta asiaan. Kiinnostava ja toivottavasti ajatuksia herättävä juttu tämä on silti.

Saat tekstiviestin tuntemattomalta paiholalaiselta pankkineuvojalta. Hän kertoo, että Härrä oyj:n osakekurssi nousee päivän loppuun mennessä. Et varsinaisesti seuraa pörssikursseja etkä muutenkaan ole mikään pien- tai suursijoittaja. Yllättävä viesti kuitenkin herättää kiinnostuksesi, ja käyt katsomassa Härrä oyj:n päivän kehityksen. Ja kyllä – kurssi on tanakassa nousussa! Seuraavana päivänä paiholalainen pankkineuvoja lähettää sinulle viestin ja sanoo, että Aatun appeen ja murkinan kurssi on laskussa. Näin myös näyttäisi olevan.

Sama toistuu parin viikon ajan. Paiholalainen pankkineuvoja osuu prognooseissaan kymmenen kertaa peräkkäin oikeaan. Onko hän satumainen pörssiguru? Pitäisikö sinun antaa raha-asiasi hänen hoidettavakseen?

Ratkaisu: Yhtä täysin oikeaa vastausta tähän kysymykseen on vaikea antaa. Periaatteessa on täysin mahdollista, että pörssiä tarkkaan seuraava toimija pystyy ymmärtämään markkinoiden liikkeitä ja ennustamaan tulevaa erinomaisestikin. Talouselämän lait ovat sellaisia.

Mutta toki taustalla voi olla myös klassinen huijaritapaus, jonka ansaintalogiikka muistuttaa hieman roskapostiviestien nigerialaiskirjeitä. Sanotaan vaikka, että pankkineuvoja lähettää ensimmäisellä kerralla 10240 viestiä eri henkilöille. Nykyään, kun tekstiviestitkin useimmiten sisältyvät puhelinlaskun kokonaissummaan, ei tuollainen määrä ole varsinaisesti mikään ongelma. Oletetaan, että puolessa viesteistä ennustetaan Härrän kurssin nousua, puolessa laskua. Ne, joiden kohdalla povaus menee pieleen, eivät enää neuvojasta kuule. Niille 5120 henkilölle, jotka puolestaan saavat oikean vinkin, lähetetään seuraava vinkki, joka toiselle kurssinousua, joka toiselle kurssilaskua. Ja niin edelleen. Kymmenen kerran jälkeen jäljellä on vielä 10 henkilöä, joista jokainen on saanut oikean vinkin joka kerralla. Jos edes joku näistä antaisi rahansa paiholalaishuijarille, voisi hän luikkia tiehensä hyvän tilin tehneenä.

Tämä pulma tuli vastaan Jordan Ellenbergin kirjassa How Not To Be Wrong, joka ilmeisesti on myös jossain vaiheessa tulossa suomeksi. Toivottavasti pian, sillä kyse on erittäin suositeltavasta opuksesta.

1

Peräkkäisten kokonaislukujen summa

|

Tämänkertainen pulmamme on kaksiosainen – viikon helppo ja viikon vaikea samassa paketissa. Löysin tämän lukuteoreettisen ongelman standup-matemaatikkona esiintyvän Matt Parkerin ensiluokkaisesta kirjasta Things To Make And Do In Fourth Dimension, ja se kuuluu seuraavasti.

Etsi lukujen 10 ja 20 väliltä ainoa kokonaisluku, jota ei voida esittää kahden tai useamman peräkkäisen positiivisen kokonaisluvun summana. Kun olet löytänyt sen, etsi sellainen (ainoa lajiaan, muuten) lukujen 30 ja 40 väliltä. Entä löydätkö lukujen 20 ja 30 väliltä tällaisia lukuja? Tässä lienee riittävästi purtavaa viikon helpon pulman tarpeisiin.

Vaikeampi pulma on tietenkin löytää kaikki sellaiset positiiviset kokonaisluvut, joita ei voida esittää peräkkäisten positiivisten lukujen summana. Entä miten tämä voidaan osoittaa?

Ratkaisu: Lukujen 10 ja 20 väliltä ainoa luku, jota ei voida esittää kahden tai useamman peräkkäisen luvun summana on 16. Lukujen 30 ja 40 väliltä löytyy tällaisista luvuista luku 32. Lukujen 20 ja 30 välillä ei tällaisia lukuja ole. Onko tässä vinkkiä tarpeeksi? Kyllä vain: kaikki muut luvut voidaan esittää peräkkäisten lukujen summina paitsi kakkosen potenssit. Todistetaan tämä:

Aloitetaan yksinkertaisesti. Kaikki parittomat luvut voidaan esittää muodossa 2n+1, missä n on jokin kokonaisluku. Tämä tarkoittaa heti sitä, että pariton luku voidaan ilmoittaa muodossa n+(n+1), eli kahden peräkkäisen luvun summana.

Siirrytään sitten parillisiin lukuihin. Jos luku on jaollinen kolmella, se voidaan ilmoittaa muodossa 3n, missä n on kokonaisluku. Toisaalta

    \[3n=(n-1)+n+(n+1),\]

joten kaikki kolmella jaolliset luvut voidaan esittää kolmen peräkkäisen luvun summana. Itse asiassa on helppo huomata, että

    \[5n=(n-2)+(n-1)+n+(n+1)+(n+2),\]

ja että sama idea yleistyy välittömästi kaikille muillekin parittomalla luvulla jaollisille kokonaisluvuille. Näin on saatu katettua jo kaikki muut luvut paitsi kakkosen potenssit (sillä kaikissa muissa parillisissa luvuissa on jokin pariton luku tekijänä). Nyt on osoitettava enää, että mitään kakkosen potensseja ei todellakaan voida kirjoittaa peräkkäisten lukujen summaksi.

Tutkitaan yleisesti k peräkkäisen kokonaisluvun summaa. Jos lukuja on pariton määrä, on summa jaollinen jollakin parittomalla luvulla, kuten edellä todettiin. Tutkitaan siis yleistä peräkkäisten lukujen summaa, jossa on parillinen määrä summan tekijöitä. Jos ensimmäinen luvuista on m, on viimeinen niistä m+(k-1). Saadaan aritmeettinen summa

    \[m+(m+1)+(m+2)+\cdots +(m+(k-1))\]

    \[=km+(0+1+2+\cdots +(k-1))\]

    \[=km+\frac{k}{2}(k-1).\]

Lavennetaan ensimmäistä termiä kakkosella ja otetaan osoittajasta k yhteiseksi tekijäksi. Saadaan

    \[km+\frac{k}{2}(k-1)=\frac{k(2m-k-1)}{2}.\]

Koska k on parillinen kokonaisluku, on tulon tekijä (2m-k-1) varmasti pariton, joten saatu luku ei voi olla kakkosen potenssi. Näin ollen kakkosen potensseja ei voida milloinkaan esittää peräkkäisten lukujen summana.

0

Venäläisen kolmion piiri

|

Ystäväni Tuomas Salo törmäsi Moskovan-vierailullaan viime vuosituhannen lopulla seuraavaan oivallisen kauniiseen pulmaan.

Valitaan mielivaltaisesti piste A positiiviselta x-akselilta väliltä ]0,1[ ja piste B positiiviselta y-akselilta väliltä ]0,1[. Valitaan piste C mistä tahansa origokeskisen yksikköympyrän kehältä koordinaatiston ensimmäisestä neljänneksestä. Osoita, että kolmion ABC piiri on enemmän kuin 2.

Ellet muuten usko, voit liikutella pisteitä oheisessa Geogebra-appletissa. Jos appletti ei näy tässä, voit leikkiä sillä Geogebratubessakin.

 

Ratkaisu: Tämän ongelman voinee ratkaista algebrallakin – Pythagoraan lausetta ja muutamia luotaantyöntäviä yhtälöitä ja niin edelleen. Seuraava ratkaisu on kuitenkin kauneudessaan ilmiömäinen ja, mikä tärkeintä, täysin riittävä.venalainenongelma

Peilataan piste C x– ja y-akseleiden suhteen pisteiksi C' ja C''.Nyt symmetrian nojalla janat AC ja AC' ovat keskenään yhtä pitkät, samoin janat BC ja BC''. Näin ollen kolmion ABC piiri on sama kuin murtoviivan C'ABC'' pituus. Koska C'C'' on ympyrän halkaisija, ja siis pituudeltaan 2, on kysytty piiri selvästi tätä pidempi.

0

Muurahaisen vaikea juoksu

|

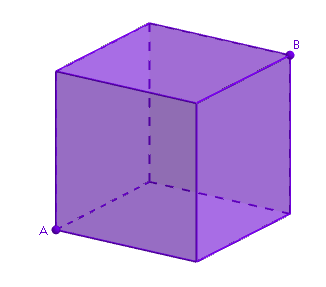KuutioMuurahainen lähtee liikkeelle kuution kärjestä A ja etenee kuution särmiä pitkin. Kun muurahainen tulee johonkin kärkeen, se valitsee sattumanvaraisesti seuraavan särmän, jota pitkin se lähtee kulkemaan (se voi siis myös palata takaisin kohti kärkeä, josta se juuri lähti). Millä todennäköisyydellä muurahainen päätyy kärkeen B kuljettuaan täsmälleen seitsemän särmää?

(HUOM! Muurahaisen ei tarvitse olla seitsemännen särmän jälkeen ensimmäistä kertaa kärjessä B.)

Tämä ongelma on huomattavasti haastavampi kuin Muurahaisen helppo juoksu, joten suosittelen tutustumaan tähän vasta helpolla juoksulla lämmiteltyäsi.

Ratkaisu: Harva ongelma (edes tässä blogissa) on saanut minut innostumaan yhtä paljoa kuin tämä. Syy siihen on seuraavassa kerrassaan hurmaavassa tavassa ratkaista pulma.

Koska kaikki kulkureitit ovat yhtä todennäköisiä, päästään ongelman ratkaisussa soveltamaan klassista todennäköisyyttä. Kun liikutaan seitsemän särmää, ja jokaisessa kärjessä on kolme vaihtoehtoa seuraavaksi suunnaksi, on erilaisia kulkureittejä tuloperiaatteen nojalla 3^7=2187 kappaletta. Selvitetään seuraavaksi, kuinka moni näistä reiteistä on suotuisia tapauksia muurahaisellemme.

Olkoon piste A=(0,0,0) ja piste B=(1,1,1). Jokaisen särmän liikkuminen muuttaa täsmälleen yhtä pisteen kolmesta koordinaatista, nollasta ykköseksi tai ykkösestä nollaksi. Tavoitteemme olisi siis se, että kaikkia koordinaatteja olisi seitsemän särmän jälkeen muutettu pariton määrä kertoja. Tämä voidaan tehdä kahdella ja vain kahdella erilaisella tavalla:

  1. Yhtä koordinaattia muutetaan viidesti ja kahta muuta kerran.
  2. Kahta koordinaattia muutetaan kolmesti ja yhtä kerran.

Lasketaan sitten, montako erilaista reittiä tapauksiin 1 ja 2 sisältyy. Viidesti muutettava koordinaatti voidaan valita kolmella tavalla. Edelleen kombinatoriikkaa soveltaen viisi vaihtoa seitsemästä voidaan valita \binom{7}{5}=\frac{7!}{5!2!}=21 tavalla. Jäljelle jäävien koordinaattien vaihdoista ensimmäinen voidaan valita kahdesta jäljellä olevasta vaihtopaikasta, jolloin viimeiselle koordinaatin vaihdolle jää vain yksi paikka. Näin ollen tapaukselle 1 suotuisia reittejä on

    \[3\cdot\binom{7}{5}\cdot 2\cdot 1=126.\]

Vastaavaa päättelyä noudattaen tapaukseen 2 sisältyy 3\cdot\binom{7}{3}\cdot \binom{4}{3}\cdot 1=420 mahdollista reittiä. Koska tapaukset 1 ja 2 ovat erilliset, eli niihin ei sisälly samoja reittejä, on reittien kokonaismäärä 126+420=546 Näin ollen todennäköisyys sille, että seitsemännen särmän jälkeen ollaan kärjessä B on klassisen todennäköisyyden mukaan

    \[\frac{546}{2187}=\frac{182}{729}=0,2496\ldots\approx 0,25.\]

Tästäkin ongelmasta iso kiitos Thomas Poveylle, jonka pulmakirjaa Professor Povey’s Perplexing Problems olen nyt pari viikkoa iltaisin jatkuvasti selaillut. Kirjassa on kymmeniä tiukkoja matematiikan ja fysiikan tehtäviä, jotka on suunnattu korkeakouluopintojen kynnyksellä oleville ongelmanratkaisusta innostuneille opiskelijoille. Tai sitten heidän opettajilleen. Erittäin suositeltava opus.

PS. Eräs opiskelijani heitti suunnilleen välittömästi ongelman kuultuaan arvauksen, että vastaus ei varmaankaan ole \frac{1}{4}, mutta että se on sinnepäin. Aivan oikein. Parittomalla siirtomäärällä kuutiossa on vain neljä kärkeä, joissa muurahainen voi olla. Mitä suuremmaksi siirtojen määrä kasvaa – kunhan niitä on vain pariton määrä – sitä lähempänä todennäköisyys päätyä kärkeen B on arvoa \frac{1}{4}.

6

Kaksi rahakuorta

|

Tämä ongelma liittyy oleellisesti kolmen rahakuoren pulmaan, joten suosittelen tutustumaan siihen ja sen ratkaisuun ensin. Luvassa on ensinäkemältä hämmästyttävä paradoksi.

Saat kirjekuoren, jossa on tietty määrä rahaa. Minulla on suljettu kirjekuori, jossa on joko kaksi kertaa enemmän rahaa kuin sinun kuoressasi tai vain puolet rahoistasi. Kannattaako sinun vaihtaa?

Päätellään kuten kolmen kuoren ongelmassa, että vaihtaminen kannattaa:

  1. Olkoon kuoressasi X euroa.
  2. Rahasumma X voi olla joko suurempi tai pienempi kuin toisen kuoren rahasumma.
  3. Toisen kuoren rahasumma on siis \frac{X}{2} todennäköisyydellä \frac{1}{2} tai 2X todennäköisyydellä \frac{1}{2}.
  4. Näin ollen rahasumman odotusarvoksi saadaan \frac{1}{2}\cdot \frac{X}{2}+\frac{1}{2}\cdot 2X=\frac{5}{4}X.

Uskomaton tulos! Tämä sotii vahvasti arkista järkeilyä vastaan. Onko vika päättelyssä vai arkijärjessä?

Ratkaisu: Tällä kerralla ongelma todella on päättelyssä, tarkemmin sanottuna kohdassa 3. Emme voi lähteä siitä, että toisessa kuoressa olisi 2X tai \frac{1}{2}X ja laskea odotusarvoa kuten kolmen kuoren ongelmassa. Tämä siksi, että ne molemmat eivät ole mahdollisia tapauksia.

Oikeaa päättelyä olisi todeta, että on kaksi rahakuorta, joissa on rahasummat X ja 2X, mutta emme tiedä, kumpi niistä on hallussamme. Nyt hallussamme olevan rahasumman odotusarvo on \frac{1}{2}\cdot X+\frac{1}{2}\cdot 2X=\frac{3}{2}X, mikä puolestaan tarkoittaa, että on yhdentekevää, vaihtaako vai ei. On yhtä todennäköistä, että hallussa on iso tai pieni rahasumma, eikä se vaihtamalla muutu.

Tämänkin pulman lähteenä oli Thomas Poveyn matematiikka- ja fysiikkaongelmia käsittelevä opus Professor Povey’s Perplexing Problems.

0

Kaarien rajaama ala

|

Sain viimein käsiini Thomas Poveyn pulmakirjan nimeltä Professor Povey’s Perplexing Problems (Oneworld Publications, 2015). Jo nopealla ensi silmäilyllä ja todella pintapuolisella selailulla kävi selväksi, että nyt on käsissä helmi. Poveyn mukaan kirjan ongelmat eivät vaadi mitään lukiotason matematiikkaa kummempia menetelmiä, mutta luovaa kykyä ongelmanratkaisuun kyllä kaivataan. Tässä yksi maistiainen kirjan sisällöstä. Näyttää ihan helpolta, mutta –

Neliön sivun pituus on 2a. Sen vastakkaisista kärjistä piirretään ympyränkaaret, joiden säteet ovat a ja 2a. Mikä on kaarien rajaaman alueen pinta-ala?Näyttökuva 2015-10-9 kello 18.39.21

 

 

0

Omenapora

|

Pitkän matematiikan syksyn 2015 ylioppilaskokeessa tehtävänä 7 kysyttiin seuraavaa:

Täysin pyöreän geenimanipuloidun omenan säde on 5,0 cm. Omenan läpi porataan sen keskeltä kulkeva reikä, jonka säde on 1,0 cm. Kuinka monta prosenttia omenan tilavuudesta tällöin häviää? Anna vastaus prosenttiyksikön kymmenesosan tarkkuudella.

Tehtävä on ihan hauska ja hyvä, mutta vielä hauskempi on tehtävän ilkeä äitipuoli. Jos olisin Martin Gardner, olisin kysynyt abiturienteilta näin:

Pallon muotoisen omenan läpi porataan kuusi senttimetriä pitkä reikä, joka kulkee pallon keskipisteen kautta. Kuinka suuri on jäljelle jäävän omenan tilavuus?

Kuva: Alan Levine/Flickr (CC BY 2.0)

Kuva: Alan Levine/Flickr (CC BY 2.0)

Ratkaisu:

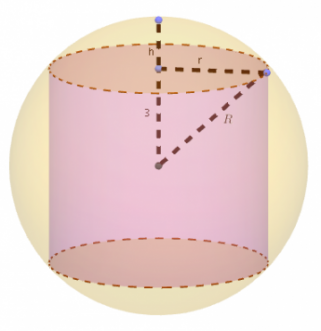
Lieriö pallossaPallo ja lieriö – poikkileikkaus

Omenapora leikkaa omenasta kappaleen, joka muodostuu suorasta ympyrälieriöstä, jonka korkeus on mainittu 6 cm, sekä kahdesta pallosegmentistä. Olkoon omenan säde R, lieriön säde r ja pallosegmentin korkeus h. Lieriö sijaitsee symmetrisesti omenan keskipisteen ylä- ja alapuolella, joten voimme piirtää oheisen poikkileikkauksen mukaisen kuvan. Nyt Pythagoraan lauseen nojalla R^2=3^2+r^2, eli r^2=R^2-3^2. Edelleen havaitaan, että pallosegmentin korkeus on h=R-3. Näistä huomioista saadaankin jo laskettua sekä lieriön että pallosegmentin tilavuudet:

    \[\begin{array}{rcl} V_l & = &\pi r^2\cdot 6=\pi(R^2-3^2)\cdot 6\\ & = & 6\pi R^2-54\pi;\\ V_{ps} & = & \pi h^2\left(R-\frac{h}{3}\right)\\ &=&\pi (R-3)^2\left(R-\frac{R-3}{3}\right)\\ & =&\frac{2}{3}\pi R^3-6\pi R^2+18\pi. \end{array}\]

Tämän jälkeen loppu on pelkkää sievennystä:

    \[\begin{array}{rcl} V_{omena} & =&V_{pallo}-V_l-2V_{ps}\\ &=&\frac{4}{3}\pi R^3-\left(6\pi R^2-54\pi\right)-2\left(\frac{2}{3}\pi R^3-6\pi R^2+18\pi\right)\\ &=&36\pi. \end{array}\]

Vastaus on siis – ehkä hieman yllättäen – omenan säteestä riippumaton vakio.

Jälkikirjoitus: Annoin tämän ongelman viime keväänä pohdittavaksi parille opiskelijalleni. Eräs heistä esitti ongelmaan sangen ketterän ratkaisun. Hän totesi, että pienentämällä reiän sädettä kohti nollaa on päädyttävä samaan ratkaisuun kuin missä muussa tapauksessa tahansa. Reiän ja pallosegmenttien hävitessä raja-arvona on pallo, jonka halkaisija on 6. Siispä jäljelle jäävä tilavuus on sama kuin 3-säteisen pallon, eli \displaystyle\frac{4}{3}\pi\cdot 3^3=36\pi. Ratkaisu on sinänsä ovela oikotie, mutta se perustuu ehkä vähän kyseenalaiseen lisäoletukseen: voimmeko tehtävänannon perusteella luotettavasti päätellä, että kyseessä on ongelma, johon on olemassa yksikäsitteinen ratkaisu?

4

Pyöreän pöydän ritarit

|

Suuren salin pyöreän pöydän ympärillä oli 24 tasaisin välimatkoin aseteltua nimettyä paikkaa. Kun pyöreän pöydän ritarit saapuivat saliin, oli valitettavasti pimeää, ja kaikki ritarit istuivat vahingossa väärille paikoille. Osoita, että pöytää kiertämällä saadaan ainakin kahden ritarin nimilaput oikeille paikoille.

Tämä ongelma löytyi Matthew Scroggsin pulmasivuilta. Hän itse kreditoi ongelman kenellepä muullekaan kuin Martin Gardnerille. Pulman ratkaisu löytyy täältä.

Evrard d’Espinques (noin v. 1470): Kuningas Arthur ja pyöreän pöydän ritarit (Kuvalähde: Wikimedia Commons/Public Domain)

0

Viiniä kuninkaan juhliin

|

Kuninkaalla oli suuret syntymäpäiväjuhlat tulossa. Hän oli varannut juhlia varten 1000 tynnyrillistä viiniä kellariinsa. Mutta viikkoa ennen juhlia alkoi hovissa levitä huhu, että yksi tynnyreistä olisi myrkytetty. Myrkky oli niin voimakasta, että pisarakin viiniä saastuneesta tynnyristä riittäisi kasvattamaan viisimetriset sierainkarvat kaikille tynnyristä siemailleille. Pahinta oli, että vaikka myrkyn vaikutus sitä juoneelle oli sataprosenttisen varma, myrkytyksen itämisaika oli jotain yhdestä vuorokaudesta kuuteen vuorokautta, eikä ennen sierainkarvojen äkillistä kasvua voinut mitenkään päätellä, oliko nauttinut myrkytettyä viiniä vai ei. Kuningas päättää testata viinikellarinsa ministereillään. Mikä on vähin määrä ministereitä, joka kuninkaan on uhrattava, jotta hän varmasti saisi selville, mikä tynnyreistä on myrkytetty?

Kuvaskannaus: JPS68/Wikimedia Commons (Public domain)

Ongelman ratkaisu löytyy täältä.

0

Rahojen punnitus

|

Kahdestatoista samannäköisestä rahasta yksi on väärennetty. Se on joko hieman liian kevyt tai liian painava. Käytettävissä on tasapainovaaka. Mikä on vähin määrä punnituksia, jolla voit varmasti selvittää, mikä rahoista on väärä ja onko se liian kevyt vai liian painava?

Tämäntyyppiset punnitusongelmat ovat hyvin klassista ongelmamatematiikkaa. Kiitoksia pulmasta Johannes Jermakalle Australiaan! Ongelman ratkaisu on tässä.

Kuva: Michael Coughlan/Flickr (CC BY-SA)

Kuva: Michael Coghlan/Flickr (CC BY-SA)