Viimekertaisessa viikon vaikeassa viisi piraattia yritti päästä sopuun aarteen jakamisesta. Tämä aiheutti ymmärrettävästi pientä närää miesjoukon kesken. Niinpä tunteet olivatkin valmiiksi pinnassa, kun heitä kohtasi onnettomuus: heidän laivansa oli vuoro ajaa karille ja upota. Piraatit onnistuivat ajelehtimaan laudankappaleen varassa pienelle saarelle, jossa he lopen väsyneinä huomasivat, että saari oli täysin autio lukuunottamatta apinaa, joka leikki kookospähkinöillä. Kookospähkinöiden ohella muuta ravintoa ei ollut saatavilla. Piraatit sopivat, että kookospähkinät jaettaisiin aamulla tasan kaikkien kesken.
Ensimmäinen piraatti kuitenkin heräsi keskellä yötä. Hän ajatteli, että kukaan ei huomaisi, jos hän ottaisi oman osuutensa kookoksista jo nyt. Hän jakoi kookokset viiteen osaan, piilotti omansa ja palautti loput kasaan. Yksi kookospähkinä jäi ylitse, ja hän antoi sen apinalle. Sitten piraatti meni takaisin nukkumaan.
Toinen piraatti heräsi vähän myöhemmin. Hänkin jakoi kookokset viiteen osaan ja hautasi oman osuutensa syrjemmälle. Myös nyt jäi yksi kookospähkinä ylitse, ja hän antoi sen apinalle.

Kuva: Loke Seng Hon/Wikimedia Commons (CC BY-SA 3.0)
Ja kuten arvata saattaa, vuorollaan yön mittaan myös kolmas, neljäs ja viides piraatti kävivät erottelemassa oman osuutensa. Myös jokainen heistä antoi yhden ylimääräisen kookoksen apinalle.
Aamulla piraatit heräsivät ja huomasivat, että kookospähkinäkasa oli yön mittaan hieman vajunut. He eivät kuitenkaan sanoneet mitään, vaan jakoivat kookokset viiteen osaan. Apinakaan ei jäänyt ilman: yksi kookos jäi ylitse.
Kuinka monta kookospähkinää saarella vähintään oli?
Ratkaisu: Tämä ongelma voidaan ratkaista ainakin parilla eri tavalla. Puhdas kokeileminen eri kookospähkinämäärillä on tietenkin yksi mahdollisuus, mutta luulenpa, että kärsivällisyyden rajat tulevat vastaan…
Lähdetään mieluummin mallintamaan tilannetta. Olkoon kookospähkinöiden lukumäärä 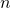 . Apina saa siis jokaisella jakokierroksella yhden pähkinän, jolloin eri jakokerroista saadaan seuraava taulukko.
. Apina saa siis jokaisella jakokierroksella yhden pähkinän, jolloin eri jakokerroista saadaan seuraava taulukko.
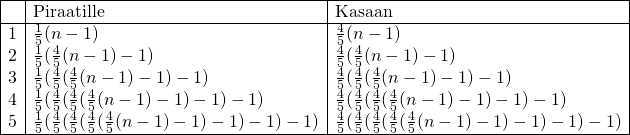
No niin. Aamulla tilanne on siis tämä, eikä yhdelläkään unenpöpperöisellä merirosmolla ole enää mukavaa näiden lausekkeiden kanssa. Tilanne ei ole ollenkaan niin paha kuin miltä se näyttää, sillä voidaan sanoa, että jollakin kokonaisluvulla 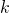 pätee
pätee
![Rendered by QuickLaTeX.com \[\frac{4}{5}\left(\frac{4}{5}\left(\frac{4}{5}\left(\frac{4}{5}\left(\frac{4}{5}\left(n-1\right)-1\right)-1\right)-1\right)-1\right)=5k+1,\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-65588d261dd253054c8e6bda0b2cebd7_l3.png)
eli jos apina saa yhden kookoksen, on jaettava kookoskasa viidellä jaollinen. Nyt yhtälön vasemmalle puolelle muodostuu geometrinen summa, jonka suhdeluku on 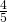 :
:
![Rendered by QuickLaTeX.com \[\left(\frac{4}{5}\right)^5 n-\left(\frac{4}{5}\right)^5-\left(\frac{4}{5}\right)^4-\left(\frac{4}{5}\right)^3-\left(\frac{4}{5}\right)^2-\frac{4}{5}\right=5k+1,\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-1203f9081d76ca7f0d04d3692e3b2e99_l3.png)
josta geometrisen summan laskukaavaa hyödyntäen saamme
![Rendered by QuickLaTeX.com \[\left(\frac{4}{5}\right)^5 n-\frac{4}{5}\cdot\frac{1-\left(\frac{4}{5}\right)^5 }{1-\frac{4}{5}}=5k+1.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-d847c6e431b8e951594d21fac82fee86_l3.png)
Kun tätä yhtälöä kerrotaan puolittain luvulla 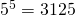 ja siirrellään hieman termejä yhtäsuuruusmerkin ylitse, saamme seuraavan Diofantoksen yhtälön:
ja siirrellään hieman termejä yhtäsuuruusmerkin ylitse, saamme seuraavan Diofantoksen yhtälön:
![Rendered by QuickLaTeX.com \[1024n=15625k+11529.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-9c3a91cdfaf6d60332d73ea2bf22c249_l3.png)
Diofantoksen yhtälöllä tarkoitetaan kokonaislukukertoimista vähintään kahden muuttujan yhtälöä, jolle etsitään kokonaislukuratkaisuja. Ne ovat saaneet nimensä noin 200-luvulla eläneen Diofantos aleksandrialaisen mukaan, joka oli aikansa merkittävimpiä matemaatikkoja. Yleistä ratkaisukaavaa näille yhtälöille ei ole olemassa, mutta joitakin erikoistapauksia voidaan ratkaista mekaanisin menetelmin. Onneksi meidän yhtälömme osuu yhteen näistä ”helpoista” tapauksista: nimittäin Diofantoksen yhtälöllä 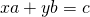 on aina ääretön määrä ratkaisuja, mikäli lukujen
on aina ääretön määrä ratkaisuja, mikäli lukujen  ja
ja 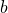 suurin yhteinen tekijä jakaa luvun
suurin yhteinen tekijä jakaa luvun  .
.
Tehdään tekninen muuttujanvaihto 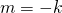 , jolloin yhtälömme voidaan kirjoittaa muotoon
, jolloin yhtälömme voidaan kirjoittaa muotoon 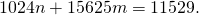 Koska
Koska 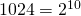 ja
ja 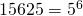 , on varmasti näiden suurin yhteinen tekijä
, on varmasti näiden suurin yhteinen tekijä 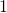 , joten ratkaisuja on olemassa. Riittää löytää pienin sellainen positiivinen arvo luvulle
, joten ratkaisuja on olemassa. Riittää löytää pienin sellainen positiivinen arvo luvulle 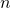 , että
, että 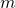 on negatiivinen.[note]Tällöin siis alkuperäinen luku
on negatiivinen.[note]Tällöin siis alkuperäinen luku 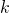 on positiivinen, kuten kuuluukin.[/note]
on positiivinen, kuten kuuluukin.[/note]
Ensin tarvitaan yksi ratkaisu yhtälölle. Tämä voidaan tehdä joko Eukleideen algoritmin avulla tai sitten ihan vain löytämällä. Äskeisestä yhtälön sievennyksestä voidaan nähdä, että jos 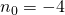 ja
ja 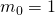 , on yhtälö tosi. Tällöin yleinen ratkaisu saadaan kaavalla
, on yhtälö tosi. Tällöin yleinen ratkaisu saadaan kaavalla
![Rendered by QuickLaTeX.com \[\begin{cases} n=-4+15625t\\ m=1-1024t \end{cases}, t\in\mathbb{Z}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-d77742a550b2daedafbc69178bc1898e_l3.png)
Nyt sijoittamalla 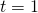 saadaan
saadaan 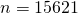 , joka on pienin mahdollinen kookospähkinöiden määrä.
, joka on pienin mahdollinen kookospähkinöiden määrä.



 Pythagoras (n. 585–496 eaa.) oli antiikin Kreikan tunnetuimpia matemaatikkoja. Hän perusti esoteerisen koulukunnan, jossa matematiikkaan sotkettiin uskonnollisia elementtejä. Pythagoralaisesta koulukunnasta on peräisin paljon tiedettä – filosofiaa, matematiikkaa, uskontotiedettä ja musiikkia.
Pythagoras (n. 585–496 eaa.) oli antiikin Kreikan tunnetuimpia matemaatikkoja. Hän perusti esoteerisen koulukunnan, jossa matematiikkaan sotkettiin uskonnollisia elementtejä. Pythagoralaisesta koulukunnasta on peräisin paljon tiedettä – filosofiaa, matematiikkaa, uskontotiedettä ja musiikkia.
![Rendered by QuickLaTeX.com \[2016=\binom{2^{\binom{2^2}{2}}}{2}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-e42b356b55fac6ad6d6138d0673f90f3_l3.png)


 On mahdollista, että neula joko putoaa reunan päälle tai sitten ei. Olkoon
On mahdollista, että neula joko putoaa reunan päälle tai sitten ei. Olkoon 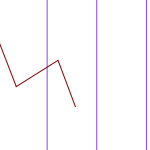 en, eli
en, eli 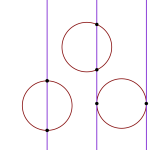 Neula, jonka pituus on
Neula, jonka pituus on 

![Rendered by QuickLaTeX.com \[\left(\frac{4}{5}\right)^5 n-\frac{4}{5}\cdot\frac{1-\left(\frac{4}{5}\right)^5 }{1-\frac{4}{5}}=5k+1.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-d847c6e431b8e951594d21fac82fee86_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} n=-4+15625t\\ m=1-1024t \end{cases}, t\in\mathbb{Z}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-d77742a550b2daedafbc69178bc1898e_l3.png)
