Viikon vaikea

0

Kissa kiinnostaa

|

Hieman olen miettinyt, kuinka paljon vielä kehtaan tänne Alex Bellosin loistavaa The Guardianin pulmapalstaa suomentaa, mutta menköön nyt vielä ainakin tämän kerran. Voi kai tätä jonkinlaisena toimituksellisena työnä sentään pitää. Tämänkertainen pulma on mukaelma muutaman vuoden takaa The New York Timesissa julkaistusta ”prinsessapulmasta”. Ja tässä se tulee.

Käytävällä on ovia rivissä, ja yhden oven takaa löytyy kissa. Kissa! Sinun tehtäväsi on löytää kyseinen luomakunnan kruunu. Mutta säännöt ovat vaativat: saat arvata vain kerran, jonka jälkeen kissa siirtyy (näennäisen!) sattumanvaraisesti yhden oven joko oikealle tai vasemmalle.

Viikon helppo pulma on löytää kissa korkeintaan neljännellä arvauksella, kun ovia on rivissä neljä.

Viikon vaikea pulma on selvästi haastavampi: mikä on pienin määrä arvauksia, joilla löydät kissan varmasti, kun kissa piileskelee seitsemän oven takana?

Selvennyksiksi vielä todettakoon, että kissa siirtyy jokaisen arvauksen jälkeen, ja että ovet ovat tosiaankin rivissä, eli vasemmanpuolimmainen ja oikeanpuolimmainen ovi ovat käytävän reunoilla, eikä niistä ole yhteyttä toisiinsa ”nurkan ympäri”.

Kuva: Abby Rosenberg / Flickr (CC BY-NC 2.0)

Ratkaisu: Tämä pulma on erinomainen esimerkki eräästä matemaattisesta ongelmanratkaisumenetelmästä, jossa monimutkaista pulmaa lähestytään ennen yksinkertaisemman erikoistapauksen kautta ja sitten pyritään löytämään menetelmä, joka sopii myös monimutkaisemmille tapauksille. Ajatellaanpa vaikka tätä pulmaa yksinkertaisimmillaan. Jos ovia olisikin vain yksi, olisi kissa varmasti sen takana. Jos taas ovia olisi kaksi, niin ellei kissa heti olisi arvatun oven takana, siirtyisi se sinne seuraavaksi kerraksi. Oikeastaan kolmen oven versio on ensimmäinen mielekäs vaihe, jossa yksi pulman lopulliselle ratkaisemiselle keskeinen idea tulee ensimmäistä kertaa esiin: jos kissa ei ole keskioven takana, on sen oltava reunassa, josta se siirtyy keskioven taakse seuraavalle kierrokselle. Kissa ei siis voi olla kahta kertaa peräkkäin reunaoven takana.

Tehdään nyt ratkaisuista kaaviokuvat. Merkitään avattua ovea A:lla ja mahdollista kissan paikkaa K:lla. Esittelen tässä nyt pisimmät tiet – kissahan voisi hyvällä onnella tulla vastaan jo aiemminkin. Mutta seuraavat reitit johtavat varmasti ratkaisuun. Neljän oven ratkaisualgoritmi on seuraava:

    \[\begin{array}{|c|c|c|c|}K&A&K&K\\ \hline&K&A&K\\ \hline K&&A&\\ \hline &A&&\end{array}\]

Pienellä pohdinnalla ratkaisumalli alkaa hahmottua. Muutamia huomioita voi tehdä nopeasti. Ei kannata aloittaa reunalta, se ei johda mihinkään. Jos kissa on reunalla, ei se voi seuraavalla kerralla siellä olla. Jos tästä laajennetaan viiden oven tapaukseen, huomataan myös se, että keskimmäisestä ovesta aloittaminen ei myöskään toimi. Miten voidaan alkaa rajoittaa kissan paikkoja? Voidaanko osa ovista rajata pysyvästi kissavapaaksi alueeksi?

Itse painin aika tovin viiden oven ongelman kanssa, mutta sitten juttu alkoi aueta. Sen innoittamana kuuden oven versio ratkesi nopeasti, eikä seitsemän ovea ollut sitten enää sen kummempi haaste. Alex Bellosin linkkaaman alkuperäisen pulman ovien lukumäärä oli 17, mutta sama ratkaisualgoritmi toimii siihenkin. Jos ovia on k kappaletta, arvauksia tarvitaan aina korkeintaan 2k-4. Tässä ratkaisu seitsemälle ovelle. Arvauksia tarvitaan korkeintaan kymmenen. En selitä enempää. Tutki itse (ja tule vasta sitten tarkistamaan ratkaisu)!

    \[\begin{array}{|c|c|c|c|c|c|c|}K&A&K&K&K&K&K\\ \hline &K&A&K&K&K&K\\ \hline K&&K&A&K&K&K\\ \hline &K&&K&A&K&K\\ \hline K&&K&&K&A&K\\ \hline&K&&K&&A&\\ \hline K&&K&&A&&\\ \hline &K&&A&&&\\ \hline K&&A&&&&\\ \hline &A&&&&&\end{array}\]

0

Pythagoraan piirakka

|

Kaikkihan me tunnemme Pythagoraan, tuon antiikin Kreikassa eläneen oppineen, jonka nimiin pantu lause (jota hän ei tietenkään ole itse keksinyt) on keskeistä koulugeometriaa peruskoulusta alkaen. Pythagoras on myös hollantilainen matematiikkalehti, joka on ilmestynyt jo 1960-luvun alusta alkaen. Seuraava Pythagoras-lehdessä julkaistu hieno pulma tuli vastaan Alex Bellosin pulmapalstalla The Guardianissa.

Isoissa juhlissa on hillittömän kokoinen piirakka. Ensimmäinen juhlavieras saa yhden prosentin piirakasta, seuraava kaksi prosenttia jäljellä olevasta piirakasta, kolmas kolme prosenttia jäljellä olevasta piirakasta ja niin edelleen, kunnes sadas vieras saa koko viimeisen palan. Kuka saa suurimman palan?

No niin, tämä pulma olisi tietenkin helppo ratkaista tietokoneen tai laskimen avulla laskemalla likiarvot kaikista paloista suhteessa koko piirakkaan, mutta itse ajattelin, että tähän täytyy olla joku kiinnostavampikin ratkaisutapa. Ja tovin pohdittuani sellaisen löysinkin: tehtävä ratkeaa pelkkää kynää ja paperia käyttäen, eivätkä tarvittavat laskutoimitukset ole lukion pitkän matematiikan kakkoskurssin tasoa hankalampia. Onnea matkaan!

Kuva: Ruth Hartnup / Flickr (CC BY 2.0)

Ratkaisu: Kymmenes vieras saa suurimman palan. Osoitetaan tämä tutkimalla peräkkäisten osuuksien suhteellisia kokoja. Näytetään siis, että kymmenenteen vieraaseen asti palaset kasvavat ja sen jälkeen ne pienenevät.

Olkoon jäljellä olevan piirakan määrä vieraan k vuorolla P. Näin ollen vieraan k osuus on \frac{k}{100}\cdot P. Piirakkaa jää jäljelle \frac{100-k}{100}\cdot P, josta seuraavan vieraan palan suuruus on näin ollen \frac{k+1}{100}\cdot\frac{100-k}{100}\cdot P. Ratkaistaan nyt epäyhtälö

    \[\frac{k}{100}\cdot P>\frac{k+1}{100}\cdot \frac{100-k}{100}\cdot P.\]

Positiivisena lukuna P voidaan jakaa nyt pois. Kun epäyhtälö kerrotaan 10000:lla ja siirretään kaikki termit samalle puolelle, saadaan muoto

    \[k^2+k-100>0.\]

Vasemmanpuoleisen lausekkeen nollakohdat ovat

    \[k=\frac{-1\pm\sqrt{401}}{2}.\]

Tässä vaiheessa tavalliset ihmiset viimeistään tarttuisivat laskimeen, mutta meidän tapauksessamme se ei ole tarpeen – olihan tavoitteemme ratkoa koko pulma vain kynän ja paperin avulla. Nyt \sqrt{400}=20, joten \sqrt{401} on vain vähän enemmän (joka tapauksessa reilusti alle 21). Siis lausekkeemme nollakohdat ovat riittävällä tarkkuudella k\approx -10,5 ja k\approx 9,5. Koska lausekkeen k^2+k-100 kuvaaja on ylöspäin aukeava paraabeli, epäyhtälön k^2+k-100>0 ratkaisujoukkona ovat (suunnilleen) välit k<-10,5 ja k>9,5 (joista negatiivisella vaihtoehdolla ei kannaltamme ole väliä).

Tulkitaan tämä ratkaisu. Alkuperäinen epäyhtälömme vastaa kysymykseen, milloin edellinen pala on seuraavaa suurempi. Saamastamme ratkaisusta voidaan päätellä, että tämä on totta suunnilleen k:n arvosta 9,5 alkaen. Koska k saa vain kokonaislukuarvoja, pätee tulos siis arvosta k=10 alkaen. Kymmenes pala on siis suurempi kuin yhdestoista, mutta yhdeksäs pala ei ole suurempi kuin kymmenes. Suurimman palan saa siis kymmenes vieras, sillä kymmenes on suurempi kuin yhdestoista, joka taas on suurempi kuin kahdestoista joka on suurempi kuin kolmastoista ja niin edelleen.

Toki kaikkien osuuksien likiarvotkin on helppo laskea, ei tosin ilman apuvälineitä. Oheisen taulukon luontiin Excelillä ei mennyt kuin hetki. Kymmenes vieras rohmuaa melkein 6,3 prosenttia koko piirakasta. Jos se jotakuta nyt kiinnostaa.

Piirakkaosuudet

0

Kolikonkääntötemppu

|

Edessäsi on 20 kolikkoa, joista 10 on kruunapuoli ylöspäin ja 10 klaavapuoli ylöspäin. Kolikoiden järjestys on satunnainen. Tehtävänäsi on jakaa kolikot kahteen kasaan niin, että niissä molemmissa olisi yhtä monta kruunaa ja yhtä monta klaavaa. Tehtävähän olisi naurettavan helppo, jos saisit katsoa kolikoita, mutta emmehän me sellaista salli.

Viikon vaikea pulma on hoitaa homma sidotuin silmin. Saat siirrellä kolikkoja haluamallasi tavalla ja käännellä niitä kummin päin hyvänsä. Kolikosta ei voi tunnustelemalla päätellä, onko se kruuna vai klaava. Ja nyt pitäisi siis tehdä kaksi kolikkoryhmää, joissa molemmissa olisi yhtä monta kruunaa ja yhtä monta klaavaa. Onnistutko?

Ratkaisu: Erota kymmenen kolikkoa ja käännä ne. Käännetyistä kolikoista yhtä moni on klaavoja kuin kääntämättömistä, samoin yhtä monta on kruunia kuin kääntämättömistä. Tämä on vanha matemaattinen trikki, josta esim. Martin Gardner on kirjoittanut. Hän tosin teki tempun korttipakalla.

0

Todennäköisyyksiä turnauskaaviosta

|

Pulmakulmassa järjestettiin pulmanratkontaturnajaiset. Lähes kaikki Pulmakulman tunnetut lukijat1 asetettiin turnauskaavioon, josta vain voitolla pääsee etenemään seuraavalle kierrokselle (katso esimerkki ohessa). Turnauskaavion todennäköisyysmatematiikasta saa aikaiseksi muutamia sangen mukavia pulmia. Seuraavat on poimittu Frederick Mostellerin kirjasta Fifty Challenging Problems in Probability.

Ensimmäisen kierroksen pulma on, millä todennäköisyydellä toiseksi paras ratkoja tulee kahdeksan pelaajan turnauksessa toiseksi, kun kaavion ensimmäinen kierros arvotaan.

Toisella kierroksella kysymme, millä todennäköisyydellä kaksi tiettyä pelaajaa (esim. Petri ja Toni) kohtaavat toisensa kahdeksan hengen pelaajan turnauksessa. Finaalikysymyksenä on, millä todennäköisyydellä kaksi tiettyä pelaajaa kohtaavat toisensa 2^n pelaajan turnauksessa.

Esimerkki turnauskaaviosta (Tehty osoitteessa http://www.freebracketgenerator.com)

Ratkaisu: Ensimmäinen kysymyksistämme on helppo: jos oletetaan, että ratkojilla on pysyvä paremmuusjärjestys (eli parempi voittaa aina heikomman), tulee toiseksi paras toiseksi vain, jos ei kohtaa parasta ennen kolmatta kierrosta eli finaalia. Näin ollen toiseksi parhaan pitää olla eri puolella kaaviota. Tämän todennäköisyys on \frac{4}{7}.

Toisessa ja kolmannessa kysymyksessä ei enää ole paremmuusjärjestyksellä väliä, nyt oletamme, että kummallakin otteluparin osapuolella on yhtäläiset mahdollisuudet jatkaa seuraavalle kierrokselle.

Olkoon Petri sijoitettu sattumanvaraiseen paikkaan kahdeksanpaikkaisessa kaaviossa. Nyt todennäköisyys, että Toni tulee ensimmäisessä ottelussa häntä vastaan, on \frac{1}{7}. Todennäköisyys sille, että Toni on viereisessä parissa (jolloin he kohtaisivat toisella kierroksella), on \frac{2}{7}, ja todennäköisyys sille, että molemmat pääsevät toiselle kierrokselle on \left(\frac{1}{2}\right)^2=\frac{1}{4}. Edelleen todennäköisyys sille, että Toni ja Petri ovat kaavion eri puolilla (jolloin he kohtaavat aikaisintaan finaalissa), on \frac{4}{7}, ja todennäköisyys, että molemmat etenevät finaaliin saakka, on \left(\frac{1}{4}\right)^2=\frac{1}{16}. Kaikkiaan Petrin ja Tonin kohtaamisen todennäköisyys on nyt

    \[\frac{1}{7}\cdot 1+\frac{2}{7}\cdot\frac{1}{4}+\frac{4}{7}\cdot\frac{1}{16}=\frac{1}{4}.\]

Ratkaistaan sitten vielä viimeinen kysymys. Jos turnauksessa on kaksi osallistujaa, kohtaavat Petri ja Toni varmasti. 2^2=4 osallistujan tapauksessa he kohtaavat todennäköisyydellä \frac{1}{2}, ja äsken näytimme, että kohtaamistodennäköisyys 2^3=8 osallistujan turnauksessa on \frac{1}{4}. Voimme tehdä arvauksen, että 2^n osallistujan turnauksessa kohtaamistodennäköisyys olisi \frac{1}{2^{n-1}}. Tämä voidaan osoittaa matemaattisella induktiolla.

Selvästi väittämämme pätee, kun n=1, eli 2^1=2 osallistujan turnauksessa Toni ja Petri kohtaavat todennäköisyydellä \frac{1}{2^{1-1}}=1. Käytetään nyt induktio-oletuksena, että 2^k osallistujan turnauksessa kohtaamistodennäköisyys olisi \frac{1}{2^{k-1}}. On osoitettava vielä, että 2^{k+1} osallistujan turnauksessa kohtaamistodennäköisyys olisi \frac{1}{2^{(k+1)-1}}=\frac{1}{2^k}.

Aloitetaan toteamalla, että jos osallistujia on 2^{k+1}, ovat Petri ja Toni eri puolilla kaaviota (eli kohtaavat aikaisintaan finaalissa) todennäköisyydellä \frac{2^k}{2^{k+1}-1}. Tämä on johdettavissa helposti kahdeksan pelaajan turnauksen mallinnuksen mukaisesti. Finaaliin päästäkseen Tonin ja Petrin on kummankin voitettava k vastustajaa, minkä todennäköisyys on \frac{1}{2^k}\cdot\frac{1}{2^k}=\frac{1}{2^{2k}}. Näin ollen todennäköisyys sille, että he ovat kaavion eri puolilla ja kohtaavat (finaalissa) on

    \[\frac{2^k}{2^{k+1}-1}\cdot\frac{1}{2^{2k}}.\]

Todennäköisyys sille, että Toni ja Petri ovat samalla puolella kaaviota, eli kohtaamassa ennen finaalia on \frac{2^k-1}{2^{k+1}-1}. Induktio-oletuksen mukaan heidän todennäköisyytensä kohdata tässä 2^k osallistujan (ali-)turnauksessa on \frac{1}{2^{k-1}}. Näin ollen yhteenlasketuksi kohtaamistodennäköisyydeksi 2^{k+1} osallistujan turnauksessa saadaan

    \[\frac{2^k-1}{2^{k+1}-1}\cdot\frac{1}{2^{k-1}}+\frac{2^k}{2^{k+1}-1}\cdot\frac{1}{2^{2k}},\]

joka toden totta sievenee muotoon

\frac{1}{2^k}.

Näin ollen induktioväite on osoitettu todeksi ja samoin koko väittämä.

2

Kolmion ja neliön piiri

|

Pitkän matematiikan tämänkeväisessä preliminäärikokeessa oli yksi kaunis tehtävä, josta saadaan mukava viikon vaikea pulma. Näin se kuuluu:

Neliöllä ja suorakulmaisella kolmiolla on sama pinta-ala. Kumman piiri on pidempi?

Kuva: Joost Markerink / Flickr (CC BY 2.0)

 

0

Torimyyjän tappio

|

Kuva: Phil Romans / Flickr (CC BY-NC-ND 2.0)

Seuraava pulma on kuuluisan amerikkalaisen ongelmanlaatijan Sam Loydin (1841–1911) käsialaa, ja se tunnetaan myös Covent Gardenin ongelmana. Näin se kuuluu:

Tolvanen ja Penttinen myyvät omenoita torilla. Heillä on yhtä paljon omenoita, mutta Penttisen omenat ovat isompia. Siispä Penttinen myy kaksi omenaa eurolla, kun taas Tolvaselta saa kolme omenaa eurolla.

Eräänä päivänä Penttisen piti mennä muualle, ja hän pyysi Tolvasta myymään hänenkin omenansa. Omenakasat sekoitettiin ja hinnaksi asetettiin viisi omenaa kahdella eurolla. Seuraavana päivänä kaikki omenat oli myyty, ja oli aika jakaa potti. He olivat sopineet jakavansa omenoista saatavat rahat tasan. Mutta nyt Tolvanen ja Penttinen huomasivat, että he olivat hävinneet seitsemän euroa siihen nähden, mitä he olisivat tienanneet, jos he olisivat myyneet omenansa erikseen.

Viikon vaikea kysymys on, paljonko Penttinen hävisi myyntijärjestelyssä.

Ratkaisu: Omenoiden kokonaismäärän on oltava viidellä jaollinen, jotta ne kaikki voidaan myydä viiden kappaleen erinä. Mutta jotta omenoista voitaisiin erotella Penttisen ja Tolvasen osuudet (tasaeuroina), on omenoita oltava vähintään 60, joista Tolvanen olisi itse myydessään saanut 10 euroa 30 omenasta ja Penttinen 15 euroa 30 isommasta omenasta.

Nyt 60 omenasta he saivat yhteensä 12\cdot 2=24 euroa, joten he häviävät yhden euron siihen nähden, että olisivat myyneet omenat erikseen. Näin ollen Tolvasen myydessä molempien omenat yhteensä seitsemän euron tappiolla on omenoita ollut alun perin 7\cdot 60=420. Kummallekin kauppiaalle jää siis käteen 7\cdot 12=84 euroa. Jos Penttinen olisi myynyt 210 omenaa itsekseen, olisi hän saanut niistä 210/2=105 euroa, joten Penttinen hävisi järjestelyssä 21 euroa.

0

Nelikulmion lävistäjä

|

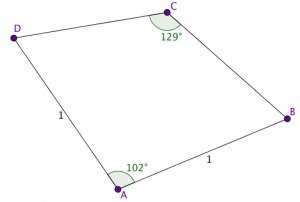
Opiskelijani Timo Hartikainen oli taannoin törmännyt Päivölän opistossa 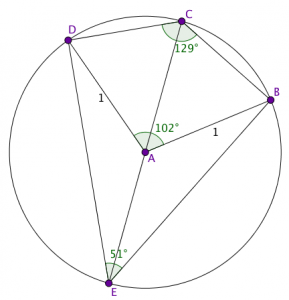Suomen matemaattisen yhdistyksen olympiavalmennuksessa kiinnostavaan ongelmaan. Tehtävänanto kuuluu seuraavasti:

Nelikulmiossa ABCD kulma \angle A=102^{\circ}, kulma \angle C=129^{\circ} ja sivut |AD|=|AB|=1. Laske lävistäjän AC pituus.

Ratkaisu: Pulman ratkaisu perustuu jännenelikulmioon, eli nelikulmioon, jonka kärjet ovat ympyrän kehällä. Nyt alkuperäinen nelikulmiomme ABCD ei ole jännenelikulmio, sillä jännenelikulmiossa vastakkaisten kulmien summa on aina 180^{\circ}. Sen sijaan jos täydennämme kuvaa niin, että mukaan tulee kärki E, jossa on 51^{\circ} kulma, tilanne muuttuu. Nyt koska 51^{\circ}=\frac{102^{\circ}}{2}, ja koska ympyrän keskuskulma on kaksinkertainen samaa kaarta vastaavaan kehäkulmaan verrattuna, on A keskipiste ympyrälle, jonka sisään piirretty jännenelikulmio EBCD on. Koska |AB|=|AD|=1, on myös AC=1, sillä sekin on ympyrän säde.

0

Kadonnut luku

|

kummalukuTämä erityisen kaunis pulma on peräisin Nob Yoshigaharalta (1930–2004), japanilaiselta ongelmaspesialistilta. Minä löysin sen jälleen kerran Alex Bellosin kautta.

Mikä luku sopii kysymysmerkin paikalle? Alhaalla oleva luku 7 ei ole virhe.

Ratkaisu: Puuttuva luku on 12. Se on siihen johtavien lukujen numeroiden summa, kuten kaikissa muissakin kohdissa.

0

Sata lanttia

|

Antti ja Petri pelaavat kiehtovaa rahapeliä: he ovat asettaneet sata kolikkoa riviin ja alkavat nostaa niitä yksi kerrallaan itselleen. Kolikot ovat kaikenlaisia viisisenttisistä kahden euron arvoisiin ja ne ovat satunnaisessa järjestyksessä. Sääntöihin kuuluu, että vuorollaan saa ottaa vain rivin reunimmaisen kolikon; kummasta tahansa päästä riviä saa nostaa.  Pelin voittaa se, kumpi saa kerättyä enemmän rahaa.

Antti aloittaa. Osoita, että Antti voi kerätä aina vähintään yhtä paljon rahaa kuin Petri.

Kuva: Branko Collin / Flickr (CC BY-SA 2.0)

Kuva: Branko Collin / Flickr (CC BY-SA 2.0)

Ratkaisu: Numeroidaan kolikot yhdestä sataan. Antti voi halutessaan varmasti poimia kaikki parilliset tai kaikki parittomat kolikot, sillä hänen haluamansa järjestysluku löytyy varmasti aina joko jonon kärjestä tai hänniltä. Niinpä hänen riittää aluksi vain katsoa, kummat kolikot kannattaa valita.

Jos kolikoita olisi yksi enemmän, etu voi siirtyä Petrille, vaikka hän saisikin yhden kolikon vähemmän kuin Antti. Jos parillisten ja parittomien arvojen ero on suurempi kuin Antin ensimmäisen kolikon arvo, 101 kolikon pelissä Petri ei ainakaan häviäisi.

3

Järvinen, Mäkinen ja Virtanen

|

Sain käsiini Alex Bellosin upouuden pulmakirjan Can You Solve My Problems? (Guardian Books, 2016), jossa jäin ensimmäisen kerran jumiin heti ensimmäisellä sivulla (tästä ongelmasta myöhemmin lisää). Ensivaikutelma kirjasta on, että nyt ollaan pulmakirjallisuuden tulevan klassikon äärellä. Huippulaatua!

Mutta asiaan. Seuraava pulma löytyy Bellosin kirjasta. Se on laatinut Henry Ernest Dudeney, ja se on julkaistu vuonna 1930 lontoolaisessa The Strand Magazinessa.1 Dudeneyn pulma saavutti aikanaan maailmanlaajuisen suosion. Tässä se tulee.

Järvinen, Mäkinen ja Virtanen ovat junan kuljettaja, konduktööri ja myyjä, eivät tosin välttämättä tässä järjestyksessä. Sattumalta junassa matkustavat herrat Järvinen, Mäkinen ja Virtanen, joihin jatkossa viitataan arvonimellä herra. Tiedetään seuraavaa:

  • Herra Virtanen asuu Tampereella.
  • Myyjä asuu Tampereen ja Helsingin puolessavälissä.
  • Herra Mäkinen tienaa 70000 euroa vuodessa.
  • Järvinen voittaa konduktöörin biljardissa.
  • Myyjän seinänaapuri (eräs matkustajista) tienaa tasan kolminkertaisesti myyjään verrattuna.
  • Myyjän sukunimikaima asuu Helsingissä.

Viikon vaikea kysymys on tietenkin, että mikä on junan kuljettajan nimi.

Kuva: Tomi Lattu/Flickr (CC BY 2.0)

Kuva: Tomi Lattu/Flickr (CC BY 2.0)

Ratkaisu: Koska Järvinen voittaa konduktöörin biljardissa, ei Järvinen ole konduktööri. Koska herra Mäkinen tienaa tasan 70000 euroa, ei hän voi olla myyjän seinanaapuri, koska 70000 ei ole kolmella jaollinen luku. Tämän vuoksi hänen on oltava Helsingissä asuva myyjän sukunimikaima, koska herra Virtanen asuu Tampereella. Myyjä on siis Mäkinen. Ja koska Järvinen ei ole myyjä eikä konduktööri, on hän junan kuljettaja.