Viikon helppo

0

Kutsuvieraiden kättelyt

|
Kuva: Dan Beard/Cosmopolitan Magazine (Public Domain), via Wikimedia Commons

Kuva: Dan Beard/Cosmopolitan Magazine (Public Domain), via Wikimedia Commons

Palataanpa jälleen klassisten Martin Gardnerin pulmien pariin.

Kutsuilla oli minun ja puolisoni lisäksi neljä muuta pariskuntaa. Kuten kohteliasta on, osa vieraista tervehti toisiaan kutsujen aluksi kätellen. Kukaan ei kätellyt puolisoaan, eikä kukaan kätellyt kenenkään kanssa kahdesti. Kättelyiden jälkeen kysyin kaikilta muilta, kuinka monen henkilön kanssa he olivat kätelleet. Jokainen vastasi eri lukumäärän. Monenko kanssa puolisoni kätteli?

 

Ratkaisu: Yhden henkilön suurin määrä kättelyitä voi olla kahdeksan. Koska minun lisäkseni henkilöitä on yhdeksän, heidän kättelymääränsä ovat varmasti 0, 1, 2, 3, 4, 5, 6, 7 ja 8. Joukossamme on siis joku, joka kättelee kaikkia muita paitsi omaa puolisoaan. Tällöin hänen puolisonsa täytyy olla se, joka ei kättele ketään, sillä kaikki muut ovat kätelleet jo ainakin kerran.

Joukosta löytyy myös seitsemän kertaa kätellyt henkilö. Hän kättelee muita paitsi puolisoaan ja nolla kertaa kätellyttä. Nyt kaikki muut paitsi seitsenkertaisen puoliso (ja nollasti kättelevä) ovat kätelleet ainakin kahdesti. Siis seitsemän kättelyn pari on kerran kättelevä. Vastaavasti kuuden kättelyn pari on kahdesti kättelevä ja viidesti kättelevän pari kolmesti kättelevä.

Tämän jälkeen jäljelle jää pariskunta, jonka molemmat puoliskot kättelevät neljästi. Siis puolisoni ja minä.

1

Loogiset lautapelaajat

|

Ystävykset Hannu, Mikko ja Tuomo pelaavat lautapeliä. Pystytkö selvittämään herrojen pelinappuloiden värit, kun tiedetään, että ne ovat punaiset, vihreät ja violetit, ja että seuraavista väittämistä täsmälleen yksi pitää paikkansa:

  • Hannu pelaa punaisilla.
  • Mikko ei pelaa punaisilla.
  • Tuomo ei pelaa violeteilla.
Kuva: Mikko Saari / Boardgamegeek (CC BY-NC-SA 3.0)

Kuva: Mikko Saari / Boardgamegeek (CC BY-NC-SA 3.0)

Tämä pulma taitaa olla yksi modernin lauselogiikan vanhimmista, ja sen on jossakin muodossa esittänyt jo logiikan ja tietokonearitmetiikan grand old man George Boole, jonka syntymästä tuli marraskuun 2015 alussa kuluneeksi 200 vuotta.

 

Ratkaisu: Erilaisia kolmen pelivärin yhdistelmiä on vain kuusi erilaista. Nämä kaikki läpikäymällä (mikä näin pienen aineiston yhteydessä yleensä on riittävän yksinkertainen ratkaisutapa) oikea väriyhdistelmä löytyy helposti.

Toisaalta pelkkä järkeilykin vie perille. Selvästikään Hannun väri ei voi olla punainen, sillä jos olisi, myös Mikkoa koskeva väite olisi totta. Jos taas Mikko ei pelaa punaisilla, Tuomon olisi pakko pelata violeteilla, tai muuten häntä koskeva väittämä pitäisi paikkansa. Tällöin Hannu saisi punaiset, mikä olisi mahdotonta, koska myös näin tulisi kaksi totta väitettä. Siis on oltava niin, että Tuomo ei pelaa violeteilla on totta. Tällöin Mikko pelaa punaisilla ja Hannu ei, ja koska Tuomo ei pelaa violeteilla, on violetti Hannun ja vihreä Tuomon väri.

(Kyllä, tässä pulmassa esiintyneille henkilöille oikeine peliväreineen saattaa löytyä jonkinlaisia vastineita tosielämässä.)

1

Peräkkäisten kokonaislukujen summa

|

Tämänkertainen pulmamme on kaksiosainen – viikon helppo ja viikon vaikea samassa paketissa. Löysin tämän lukuteoreettisen ongelman standup-matemaatikkona esiintyvän Matt Parkerin ensiluokkaisesta kirjasta Things To Make And Do In Fourth Dimension, ja se kuuluu seuraavasti.

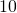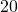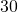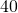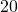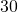Etsi lukujen 10 ja 20 väliltä ainoa kokonaisluku, jota ei voida esittää kahden tai useamman peräkkäisen positiivisen kokonaisluvun summana. Kun olet löytänyt sen, etsi sellainen (ainoa lajiaan, muuten) lukujen 30 ja 40 väliltä. Entä löydätkö lukujen 20 ja 30 väliltä tällaisia lukuja? Tässä lienee riittävästi purtavaa viikon helpon pulman tarpeisiin.

Vaikeampi pulma on tietenkin löytää kaikki sellaiset positiiviset kokonaisluvut, joita ei voida esittää peräkkäisten positiivisten lukujen summana. Entä miten tämä voidaan osoittaa?

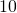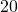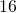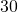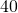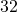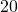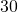Ratkaisu: Lukujen 10 ja 20 väliltä ainoa luku, jota ei voida esittää kahden tai useamman peräkkäisen luvun summana on 16. Lukujen 30 ja 40 väliltä löytyy tällaisista luvuista luku 32. Lukujen 20 ja 30 välillä ei tällaisia lukuja ole. Onko tässä vinkkiä tarpeeksi? Kyllä vain: kaikki muut luvut voidaan esittää peräkkäisten lukujen summina paitsi kakkosen potenssit. Todistetaan tämä:

Aloitetaan yksinkertaisesti. Kaikki parittomat luvut voidaan esittää muodossa 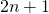2n+1, missä 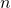n on jokin kokonaisluku. Tämä tarkoittaa heti sitä, että pariton luku voidaan ilmoittaa muodossa 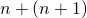n+(n+1), eli kahden peräkkäisen luvun summana.

Siirrytään sitten parillisiin lukuihin. Jos luku on jaollinen kolmella, se voidaan ilmoittaa muodossa 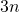3n, missä 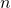n on kokonaisluku. Toisaalta

    \[3n=(n-1)+n+(n+1),\]

joten kaikki kolmella jaolliset luvut voidaan esittää kolmen peräkkäisen luvun summana. Itse asiassa on helppo huomata, että

    \[5n=(n-2)+(n-1)+n+(n+1)+(n+2),\]

ja että sama idea yleistyy välittömästi kaikille muillekin parittomalla luvulla jaollisille kokonaisluvuille. Näin on saatu katettua jo kaikki muut luvut paitsi kakkosen potenssit (sillä kaikissa muissa parillisissa luvuissa on jokin pariton luku tekijänä). Nyt on osoitettava enää, että mitään kakkosen potensseja ei todellakaan voida kirjoittaa peräkkäisten lukujen summaksi.

Tutkitaan yleisesti 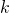k peräkkäisen kokonaisluvun summaa. Jos lukuja on pariton määrä, on summa jaollinen jollakin parittomalla luvulla, kuten edellä todettiin. Tutkitaan siis yleistä peräkkäisten lukujen summaa, jossa on parillinen määrä summan tekijöitä. Jos ensimmäinen luvuista on 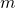m, on viimeinen niistä 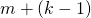m+(k-1). Saadaan aritmeettinen summa

    \[m+(m+1)+(m+2)+\cdots +(m+(k-1))\]

    \[=km+(0+1+2+\cdots +(k-1))\]

    \[=km+\frac{k}{2}(k-1).\]

Lavennetaan ensimmäistä termiä kakkosella ja otetaan osoittajasta 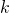k yhteiseksi tekijäksi. Saadaan

    \[km+\frac{k}{2}(k-1)=\frac{k(2m-k-1)}{2}.\]

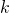Koska k on parillinen kokonaisluku, on tulon tekijä 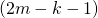(2m-k-1) varmasti pariton, joten saatu luku ei voi olla kakkosen potenssi. Näin ollen kakkosen potensseja ei voida milloinkaan esittää peräkkäisten lukujen summana.

0

Neliön kolmijako

|

Neliön yhdestä kärjestä vedetään kaksi kuvan mukaista janaa, jotka jakavat neliön kolmeen yhtä suureen osaan. Missä suhteessa janat jakavat neliön sivut?Näyttökuva 2015-11-5 kello 19.25.34

 

Ratkaisu: Sivujen jakosuhde on 2:1. Tämä on helppo huomata esimerkiksi piirtämällä neliölle lävistäjä samasta kärjestä, josta janat lähtevät. Nyt muodostuvien symmetristen kolmioiden alojen suhteen on selvästi oltava 2:1, jotta alkuperäisten janojen erottama nelikulmio olisi kolmannes koko neliön alasta. Koska kolmioilla on sama korkeusjana (neliön sivu), on alojen suhde välttämättä kannan jakosuhde.

Näyttökuva 2015-11-5 kello 19.27.07

0

Muurahaisen helppo juoksu

|

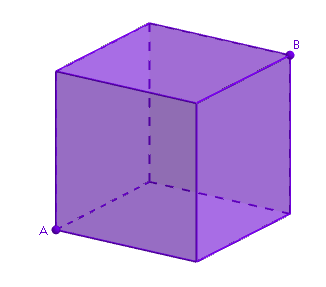KuutioMuurahainen lähtee liikkeelle kuution kärjestä A ja etenee kuution särmiä pitkin. Kun muurahainen tulee johonkin kärkeen, se valitsee sattumanvaraisesti seuraavan särmän, jota pitkin se lähtee kulkemaan (se voi siis myös palata takaisin kohti kärkeä, josta se juuri lähti). Millä todennäköisyydellä muurahainen päätyy kärkeen B täsmälleen kolme särmää kuljettuaan?

Ratkaisu: Jokaisessa kärjessä muurahaisella on kolme vaihtoehtoa seuraavalle suunnalle, joten erilaisia kolmen särmän reittejä on tuloperiaatteen mukaan 3\cdot 3\cdot 3=27.

Mietitään sitten, kuinka moni reiteistä vie kolmea särmää pitkin kärkeen B. Kärki A on ainoa kärki, josta etäisyys kärkeen B on 3 särmää. Kustakin kärjestä, johon kärjestä A pääsee, etäisyys on 2 särmää. On samantekevää, mikä suunta valitaan ensin – sopivia vaihtoehtoja on siis 3. Toisessa kärjessä on aivan sama, minne muurahainen jatkaa matkaansa, kunhan se ei palaa takaisin. Vaihtoehtoja on siis 2. Kolmannesta kärjestä on yksi reitti kärkeen B. Näin ollen suotuisia reittejä on 3\cdot 2\cdot 1=6.

Klassisen todennäköisyyden mukaan kysytty todennäköisyys on siis \frac{6}{27}=\frac{2}{9}.

No niin, tämä oli helppo. Nyt mars mars Muurahaisen vaikean juoksun pariin. Eiköhän tästä ainakin yksi tai kaksi vihjettä sen ratkaisemiseksi tullut.

2

Kolme rahakuorta

|

Seuraava pulma on jälleen Thomas Poveyn peruja. Se on sukua kuuluisalle Monty Hallin ongelmalle, mutta siinä on oma pieni lisämausteensa.

Saat kirjekuoren, jossa on tietty summa rahaa. Tämän jälkeen näytän sinulle kaksi muuta kuorta, joista toisessa on kaksinkertainen rahasumma ja toisessa puolet kirjekuoresi rahasummasta. Suljen kaksi muuta kuorta ja sekoitan ne niin, ettei niistä voi mitenkään päätellä, kumpi oli kumpi. Nyt sinulla on kaksi vaihtoehtoa: voit joko pitää nykyisen kuoresi tai vaihtaa jompaan kumpaan toisista kuorista. Mitä sinun kannattaisi tehdä?

Ratkaisu: Tutkitaan ongelmaa odotusarvon käsitteen kautta. Odotusarvo tarkoittaa eräänlaista satunnaisilmiön jakauman keskiarvoa, jota laskettaessa satunnaismuuttujan arvot painottuvat niiden todennäköisyyksien suhteessa.

Olkoon nyt kirjekuoressasi oleva rahasumma X. Näin ollen kahdessa muussa kuoressa olevat rahasummat ovat 2X sekä \frac{1}{2}X. Nyt on kaksi mahdollista tapausta.

  1. Et vaihda kuoria. Tällöin saamasi rahasumman odotusarvo on varmasti X.
  2. Vaihdat. Nyt voit todennäköisyydellä \frac{1}{2} saada kuoren, jossa on 2X, ja samoin todennäköisyydellä \frac{1}{2} kuoren, jossa on \frac{1}{2}X. Saamasi rahasumman odotusarvo on nyt \frac{1}{2}\cdot 2X+\frac{1}{2}\cdot\frac{1}{2}X=\frac{5}{4}X.

Näin ollen vaihto kannattaa.

 

2

Laskut sekaisin

|

Kiireinen yrittäjä lähettää kuudelle asiakkaalleen laskun ja sulkee ne kirjekuoriin. Äkkiä hän huomaa, että osoitetarrat unohtuivat kuorien päältä. Millä todennäköisyydellä hän saa sattumanvaraisesti lätkimistään tarroista täsmälleen viisi oikeisiin kuoriin?

Kirjuri Ezra (n. 700-l.) Kuvalähde: Wikimedia Commons/Public domain

Kirjuri Ezra (n. 700-l.) Kuvalähde: Wikimedia Commons/Public domain

Ratkaisu: Todennäköisyys on nolla. Jos viisi osoitetta menee oikein, myös kuudes menee.

0

Kolikonheittoa shakkilaudalla

|

Pyöreä kolikko pudotetaan sattumanvaraisesti suurelle shakkilaudalle. Shakkilaudan ruudun sivu on kaksinkertainen kolikon halkaisijaan verrattuna. Millä todennäköisyydellä kolikko putoaa sekä mustan että valkean ruudun päälle?

Tämä hauska pikku pulma tuli vastaan Alex Bellosin The Guardianissa pitämää pulmapalstaa selatessani. Hän puolestaan sanoi löytäneensä ongelman kirjasta, jolla on hieno nimi: Professor Povey’s Perplexing Problems. Tämä Thomas Poveyn kirja lähtikin heti tilaukseen. Pitäkää siis varanne jatkossakin, rakkaat pulmakulman lukijat!

Ratkaisu: 

Tarkastellaan shakkilautaa, jonka ruudun sivun pituus on 2a. Tällöin kolikon halkaisija on a, ja kolikkoja mahtuu kerralla yhden ruudun sisälle neljä. Tässä asetelmassa kolikkojen keskipisteet muodostavat neliön, jonka sivun pituus on a. image

Jos nyt pudotamme kolikon shakkiruudulle, ei se ulotu toisen ruudun puolelle, mikäli sen keskipiste jää tummennetun neliön sisälle. Tämän tummennetun neliön ala on \frac{1}{4} koko ruudun alasta, joten vastaus kysymykseen on tietenkin \frac{3}{4}.

2

Tornikellon lyönnit

|

Tornikello lyö 12 kertaa 30 sekunnissa. Missä ajassa kello lyö kuusi kertaa?

Kuva: Mikko Paananen/Wikipedia

Ratkaisu: 

Tornikello lyö ensimmäisen kerran ajanhetkellä 0 sekuntia ja kahdennentoista kerran ajanhetkellä 30 sekuntia. Näiden hetkien väliin jää 11 lyönninväliä, joista viidennen jälkeen kello lyö kuudennen kerran. Näin ollen kello lyö kuusi kertaa \frac{5}{11}\cdot 30=\frac{150}{11}\approx 13,6 sekunnissa.

Tähän kirjoitan nyt vielä julkisen anteeksipyynnön lukion pitkän matematiikan ykköskurssilaisilleni, jotka täysin yksimielisesti vastasivat tähän kysymykseen väärin kurssikokeessaan viime viikolla. Tiesin hieman jekuttavani teitä. Anteeksi.

4

Missä isä on?

|

Lapsi on 21 vuotta äitiään nuorempi. Tasan kuuden vuoden kuluttua äidin ikä on täsmälleen viisinkertainen lapsen ikään verrattuna. Missä lapsen isä on?

Tämä hauska ongelma löytyi uusiseelantilaiselta FOLJ.com-pulmasivustolta, jonne viime viikon vaikean punnitusongelman vinkannut Johannes Jermakka minut johdatti.

Ratkaisu:

Olkoon lapsen ikä nyt x vuotta. Tällöin äidin ikä kuuden vuoden kuluttua on 27+x, ja koska se on viisinkertainen lapsen ikään verrattuna, saadaan yhtälö

    \[27+x=5(x+6),\]

jonka ratkaisu on x=-\frac{3}{4} vuotta eli -9 kuukautta. Näin ollen lapsen isä lienee juuri siellä, missä lapsen äitikin on.