Vedamatematiikkaa

8.3.2016 | Opettaja H.

Swāmī Bhāratī Kṛṣṇa Tīrtha (1884–1960) oli intialainen uskonoppinut ja matemaatikko, joka väitti kaiken matematiikan löytyvän muinaisista hindulaisista Veda-kirjoituksista johdetuista 16 suurasta ja 13 apusuurasta. Uskoo ken tahtoo (siis sen, mitä Swāmī Bhāratī Kṛṣṇa Tīrtha 1950-luvun lopulla kirjoittamassaan teoksessa väitti), mutta joka tapauksessa nämä yksinkertaiset säkeet antavat muutamia erittäin käyttökelpoisia – ja nopeita! – kikkoja päässälaskuun.

Keskitytään nyt toiseen suuraan, jonka nimi on Nikhilam Navatashcaramam Dashatah¹. Se tarkoittaa suunnilleen, että ”kaikki yhdeksästä ja viimeinen kymmenestä”. Siinä kerrotaan kaksi lukua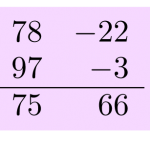 keskenään käyttäen apuna niiden etäisyyttä lähimmästä kymmenen potenssista. Kaksinumeroisilla luvuilla laskettaessa käytetään referenssilukuna sataa, kolminumeroisilla tuhatta ja niin edelleen. Otetaan esimerkiksi tulo $78\cdot 97$ . Kirjoitetaan luvut allekkain ja laitetaan niiden viereen toiseen sarakkeeseen niiden etäisyydet luvusta 100. Nyt tulon kaksi viimeistä numeroa saadaan kertomalla oikeanpuoleisen sarakkeen luvut keskenään: $-22\cdot (-3)=66$ . Jos tässä tulossa olisi enemmän kuin kaksi numeroa, menisivät sadat muistinumeroiksi alkuosuuteen, eli esimerkiksi jos oltaisiin saatu $840$ , olisivat viimeiset kaksi numeroa $40$ ja $8$ lisättäisiin tulon alkuosuuteen. Vastaavasti jos tässä tulossa olisi vähemmän kuin kaksi numeroa, lisättäisiin nollia eteen.

Toisessa vaiheessa voidaan edetä neljällä eri tavalla, jotka kaikki tuottavat saman tuloksen. Voidaan laskea saman diagonaalin luvut yhteen. Tai voidaan laskea yhteen vasemmanpuoleisen sarakkeen luvut ja vähentää $100$ . Tai edelleen voidaan laskea oikeanpuoleisen sarakkeen luvut yhteen ja lisätä $100$ . Kuinka tahansa toimitaankaan, tulos on aina sama: $78-3=97-22=78+97-100=-22-3+100=75.$ Tulon kaksi ensimmäistä numeroa ovat siis $75$ . Ja kaikkiaan $78\cdot 97=7566$ , kuten kuka tahansa voi tarkistaa.

Viikon helppona tehtävänä on osoittaa, miksi tämä menetelmä toimii aina kaksinumeroisille luvuille.

Entäpä jos tehtävänä olisikin laskea vaikkapa $103\cdot 87$ ? Tai $514\cdot 522$ ? Viikon vaikea pulma on miettiä, miten tätä samaa tekniikkaa voisi soveltaa myös näihin tuloihin.

Tämä temppu parin sukulaisensa kanssa tuli vastaan Alex Bellosin (ainakin ensimmäisen puoliskonsa perusteella aivan loistavassa) kirjassa Alex’s Adventures in Numberland (Bloomsbury, 2010).

Kulmanpuolittajien välinen kulma

17.2.2016 | Opettaja H.

Kuinka suuressa kulmassa suorakulmaisen kolmion terävien kulmien puolittajat leikkaavat? Entä yleistyykö tämä tulos myös muihin kolmioihin?

Ratkaisu: kulmanpuolittajat

Tutkitaan kolmiota $ABC$ , jonka kulma $C$ on suora. Olkoot kulman $A$ suuruus $\alpha$ ja kulman $B$ vastaavasti $\beta$ . Näin ollen $\alpha + \beta = 90^{\circ}$ . Tutkitaan sitten kulmanpuolittajien ja hypotenuusan rajaamaa kolmiota $ABD$ . Nyt koska $\frac{\alpha}{2}+\frac{\beta}{2}+\delta=180^{\circ}$ , ja koska $\frac{\alpha}{2}+\frac{\beta}{2}=\frac{90^{\circ}}{2}=45^{\circ}$ , niin välttämättä $\delta=135^{\circ}$ . Toinen kulmanpuolittajien välisistä kulmista on tämän vieruskulma, eli $45^{\circ}$ .

Tulos on aika hauska ja toimii selvästi kaikissa suorakulmaisissa kolmioissa. Ihan yhtä nätisti tämä tulos ei kaikkiin kolmioihin yleisty, sillä jos alkuperäisen kolmion kolmas kulma olisi $\gamma$ , jäisi kulmanpuolittajien välisiksi kulmiksi tällöin $90^{\circ}+\frac{\gamma}{2}$ ja $90^{\circ}-\frac{\gamma}{2}$ .

Kadonnut euro

12.2.2016 | Opettaja H.

Kolme ystävystä oli ravintolassa. Kun laskun maksamisen aika tuli, jokainen ystävyksistä maksoi yhteisestä laskusta $15$ euroa käteisellä. Kassanhoitaja huomasi kuitenkin laskuttaneensa heiltä viisi euroa liikaa ja käski tarjoilijaa palauttamaan rahan ystävyksille. Tarjoilija huomasi kuitenkin, ettei hän pystynyt jakamaan ylimääräistä viitosta tasan ystävysten kesken, joten hän turvautui röyhkeään temppuun: hän antoi kullekin ystävyksistä vain euron takaisin ja jemmasi kaksi euroa taskuunsa.

Mutta hetkinen… Ystävykset ovat nyt siis saaneet kukin euron takaisin, eli he ovat maksaneet $14$ euroa per nuppi, $3\cdot 14=42$ . Tähän lisätään tarjoilijan kähveltämät kaksi euroa, joten saadaan yhteensä $44$ euroa. Mihin yksi euro hävisi?

Ratkaisu: Tämä klassikkokompa esiintyy monissa lähteissä erilaisin variaatioin. Vastaus on tietenkin, ettei euro häviä minnekään, vaan koko kysymys on väärin aseteltu lukijan hämmentämiseksi. Ystävykset maksavat $45$ euroa. Kassanhoitaja palauttaa viisi euroa, josta tarjoilija vetää välistä kaksi. Kolme euroa palautuu ystävyksille. Nyt siis $45$ eurosta ravintola saa $40$ , tarjoilija $2$ ja ystävykset $3$ . Menitkö lankaan?

Ménage à quatre

1.2.2016 | Opettaja H.

Hyvin tunnetussa (ja varsin helpossa) matemaattisessa ongelmassa pitää kuljettaa susi, lammas ja kaali veneellä joen yli, johon soutajan lisäksi mahtuu vain yksi muu matkustaja. Jutun juju on tietenkin se, että ellei soutaja ole paikalla vahtimassa, syö susi lampaan ja lammas kaalin. Kysymys kuuluu, kuinka nämä saadaan yhtenä kappaleena joen yli. Ratkaisepa tämä ensin, ellet ole jo ratkaissut!

Ian Stewart pistää kirjassaan Another Fine Math You’ve Got Me Into… vielä paremmaksi. Nyt kuljetettavana on mörkö, susi, lammas ja kaali, eikä veneeseen edelleenkään mahdu soutajan lisäksi kuin yksi muu matkalainen. Susi syö yhä lampaan ja lammas kaalin, ellei niitä valvota. Mörkö puolestaan iskee valvomattomana välittömästi hampaansa suteen, mikäli paikalla ei ole kaalia (jota se ei syö). Saadaanko retkue toisiaan popsimatta joen toiselle penkalle?

Kuva: Hasibul Haque Sakib/Flickr (CC BY-NC 2.0)

Ratkaisu: Kuljetus onnistuu, vaikka mörkö onkin häiritsemässä. Ongelman voi ratkaista ihan päättelemälläkin, mutta mielestäni yksi kiehtova ratkaisutapa on tehdä geometrinen visualisointi tilanteesta. Näin tulkittuna ongelma on sukua taannoiselle muurahaisen vaikealle juoksulle.

Ratkaisuun tarvitaan tesseraktia eli neliulotteista hyperkuutiota, joka on muuten ihan samanlainen kuin tavallinen kolmiulotteinen kuutio, mutta sen jokaisessa kärjessä kohtaa neljä särmää kolmen sijasta.

Kuva: Sonja Šumonja/Geogebratube (CC BY-SA); muokkaus Hannu Sinisalo

Tavoitteena on päästä (kaali, lammas, susi, mörkö)-koordinaatiston pisteestä $(0, 0, 0, 0)$ pisteeseen $(1, 1, 1, 1)$ , jossa jokainen koordinaatin vaihto vaihtaa yhden siirreltävän luontokappaleen paikkaa joen yhdeltä puolelta toiselle. Jokaisen koordinaatin vaihto vastaa tesseraktin yhden särmän kulkemista. Jokaisessa tesseraktin kärjessä osa särmistä poissuljetaan mahdottomina ja lopuista valitaan reitti, jolla jatketaan eteenpäin.

Ensimmäinen siirrettävä on oltava lammas. Siis ensimmäinen piste, johon origosta päädytään on pakko olla $(0,1,0,0)$ . Tämän jälkeen viedään mörkö, eli siirrymme pisteeseen $(0,1,0,1)$ . Sitten viedään kaali siirtymällä pisteeseen $(1,1,0,1)$ ja tuodaan lammas takaisin siirrolla $(1,0,0,1)$ . Sitten viedään susi $(1,0,1,1)$ , ja lopulta viimeiseksi viedään lammas uudestaan $(1,1,1,1)$ .

Koetapa löytää ongelmaan vielä toinenkin ratkaisu – sellainen on olemassa.

Ajatustenlukutemppu

26.1.2016 | Opettaja H.

Valmistele neljä lappua tai korttia tai taulua, joihin kirjoitat seuraavat luvut:

$1, 3, 5, 7, 9, 11, 13, 15$
$2, 3, 6, 7, 10, 11, 14, 15$
$4, 5, 6, 7, 12, 13, 14, 15$
$8, 9, 10, 11, 12, 13, 14, 15$

Tämän jälkeen käske temppusi uhrin ajatella jotain kokonaislukua väliltä $1-15$ . Sitten kysyt, mistä kaikista lapuista hänen lukunsa löytyy. Tämän jälkeen pamautat välittömästi hänen ajattelemansa luvun. Saat luvun helposti laskemalla yhteen ensimmäisen luvun jokaisesta lapusta, jonka toverisi mainitsee. Jos siis vaikka hän olisi ajatellut lukua $13$ , hän olisi sanonut, että luku löytyy tauluista 1, 3 ja 4, jonka jälkeen laskisit vain $1+4+8=13$ .

Temppu on hämmästyttävän hauska ja helppo. Se tuli vastaan Rob Eastawayn ja Jeremy Wyndhamin kirjassa Why do Buses Come in Threes? Viikon helppo kysymys on tietenkin se, miksi temppu toimii.

Ratkaisu: Kuten Mikko kommentoikin, ovat tempun taustalla lukujen $1-15$ nelibittiset binääriesitykset. Esimerkiksi $13=1101_2$ , eli se saadaan laskemalla $1\cdot 2^3+1\cdot 2^2+ 0\cdot 2^1+1$ . Jokainen luku, jossa viimeinen bitti on ykkönen, on lapussa 1. Vastaavasti toiseksi viimeistä ykköstä tarvitsevat luvut ovat lapussa 2, toisen bitin ykköset lapussa 3 ja ensimmäisen bitin ykköset lapussa 4.

Temppu on kuten sanottua erittäin helppo, mutta aion käyttää sitä jatkossa opettaessani binäärilukujen käyttöä. Erittäin hyvää oppituntimateriaalia!

Pimeät sukat

7.1.2016 | Opettaja H.

Pimeän vaatehuoneen sukkalaatikossa on $16$ punaista sukkaa ja $20$ sinistä sukkaa. Montako sukkaa minun pitää vähintään laatikosta ottaa, jotta saan varmasti parin samanvärisiä sukkia?

No. Tämä oli ihan liian helppo. Laitetaan vähän lisää panoksia. Laatikossa on yhtä monta sinistä ja punaista sukkaa. Tiedetään, että pienin määrä, joka sukkia pitää nostaa laatikosta, jotta saataisiin ainakin kaksi samanväristä sukkaa, on sama kuin määrä, joka pitää nostaa, jotta saataisiin varmasti kaksi eriväristä sukkaa. Montako sukkaa laatikossa on?

Ratkaisu: Ensimmäisen kysymyksen vastaus on kolme. Toisen kysymyksen vastaus on neljä.

Tuomaan talo

21.12.2015 | Opettaja H.

Tuomas asuu kadulla, jonka talonnumerot ovat väliltä $8-100$ . Kössi tahtoo saada selville, mikä Tuomaan talon numero on.

Kössi kysyy, onko numero suurempi kuin $50$ . Tuomas vastaa, mutta valehtelee.

Seuraavaksi Kössi kysyy, onko numero jaollinen neljällä. Tuomas vastaa, mutta valehtelee taas.

Sitten Kössi kysyy, onko numero jonkin luvun neliö. Nyt, kaikkien hämmästykseksi, Tuomas vastaa totuudenmukaisesti.

Kössi sanoo, että jos Tuomas vielä kertoisi, onko ensimmäinen numero $3$ , hän tietäisi oikean talonnumeron. Tuomas vastaa Kössille, mutta emme tiedä, puhuiko hän totta. Tämän jälkeen Kössi ilmoittaa vastauksensa, joka valitettavasti on väärä.

Missä numerossa Tuomas oikeasti asuu?

Kuva: Bert Kaufmann/Flickr (CC BY-SA 2.0)

Ratkaisu: Kössi ei tietenkään tiedä, että Tuomas puhuu suurimman osan ajasta puhdasta palturia. Siksi Kössi perustaa veikkauksensa siihen, mitä Tuomas vastaa, ja se puolestaan vie meidät ratkaisun jäljille.

Koska ensimmäiseen kysymykseen Tuomas valehteli ja lopuksi Kössi haluaa tietää, onko ensimmäinen numero $3$ , on oikea talonnumero tietenkin suurempi kuin $50$ . Koska välillä $8-50$ on vain kaksi neljällä jaollista neliötä ( $16$ ja $36$ ) ja lukuisia sellaisia lukuja, jotka eivät ole joko jaollisia neljällä tai neliöitä tai kumpaakaan näistä, on Tuomas vastannut sekä neljälläjaollisuuskysymykseen (valheellisesti) että neliökysymykseen (todenmukaisesti) kyllä.

Tämä kaikki tarkoittaa sitä, että todellisuudessa Tuomas asuu talossa, jonka numero on suurempi kuin $50$ , ei ole neljällä jaollinen ja on jonkin luvun neliö. Ainoa kyseeseen tuleva talonnumero on $81$ .

Tangenttikolmio

15.12.2015 | Opettaja H.

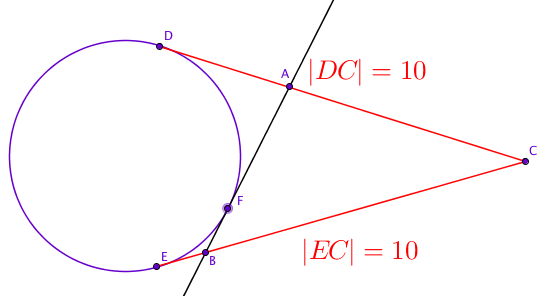Näyttökuva 2015-12-11 kello 15.46.15 Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä $C$ . Tangenttien sivuamispisteet $D$ ja $E$ ovat etäisyydellä $10$ pisteestä $C$ . Piirretään ympyrälle vielä yksi tangentti pisteiden $C$ ja $D$ välisellä kaarella olevan pisteen $F$ kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet $A$ ja $B$ . Laske kolmion $ABC$ piiri.

Martin Gardner ainakin on tätä ongelmaa esitellyt.

Ratkaisu: Aivan vastaavasti kuin piste $C$ on tangenttikulman kärki, myös pisteet $A$ ja $B$ ovat. Voidaan helposti osoittaa, että tangenttikulman kärki on aina yhtä etäällä molemmista tangenttipisteistä, eli samaan tapaan kuin $|DC|=|EC|$ , voidaan myös todeta, että $|AD|=|AF|$ ja $|BE|=|BF|$ . Siis kolmion $ABC$ piiri on $20$ .

Touko-tontun toivekierros

8.12.2015 | Opettaja H.

Touko-tonttu lähtee Korvatunturilta keräämään lapsukaisten joululahjatoiveita. Hän tarvitsee koko kierrokseensa kuusi päivää, jonka jälkeen hän on jälleen takaisin Korvatunturilla.

Valitettavasti Touko-tontun tarvitsee myös syödä matkalla. Koska silkohapsien kirjeet vievät paljon tilaa, ja koska tontun ruoka on melko painavaa, ei Touko voi kantaa mukanaan kuin neljän päivän ruokavarat. Tontunruokaa saa vain Korvatunturilta, joten Touko on vaarassa nääntyä nälkään!

Ellei sitten.

Toukohan voi ottaa mukaansa tonttukavereita Korvatunturilta! Jokainen tonttu pystyy kuitenkin kantamaan vain neljän päivän ruokavarat mukanaan ja jokainen syö päiväannoksen ruokaa joka päivä. Yhtäkään tonttua ei saa näännyttää nälkään eikä jättää matkan varrelle ja kukin tonttu saa lähteä Korvatunturilta vain kerran. Sosiaalisena eläimenä tonttu voi jakaa omista ruokavaroistaan (kokonaisia päiväannoksia) muille.

Kuinka monta tonttua Touko vähintään tarvitsee mukaansa Korvatunturilta?

Tämä ongelma osui silmiini Alex Bellosin pulmapalstalta The Guardianissa. Se on ilmeisesti saksalaista alkuperää.

Ratkaisu: On selvää, ettei Touko selviä yksin. Pienellä kokeilulla huomataan myös, että yksi kaveri ei riitä. Kaksi aputonttua sen sijaan on tarpeeksi.

Touko ja kaksi aputonttua starttaavat Korvatunturilta kontit täynnnä ruokaa. Ensimmäisen päivän jälkeen ensimmäinen aputonttu antaa yhden appeen Toukolle ja toisen toiselle tontulle. Nyt ensimmäiselle tontulle jää yksi ruoka kotimatkaa varten, Toukon ja toisen tontun ruokavarastot ovat jälleen täynnä. Toisen päivän jälkeen toinen tonttu antaa yhden päivän sapuskat Toukolle ja suuntaa kahden oman ruokapakettinsa kanssa kohti kotia. Toukolla on nyt ruokaa neljäksi päiväksi, joten loppumatkan hän selviää yksinään.

Kuunsirppi

30.11.2015 | Opettaja H.

Kuva: Thomas Bresson/Flickr (CC BY 2.0)

Seuraava pulma on peräisin professori Ian Stewartin Incredible Numbers-sovelluksesta iPadille, jossa on paljon muutakin mukavaa matemaattista opittavaa ja mietiskeltävää. Stewartin kirja Kirjeitä nuorelle matemaatikolle (Terra Cognita 2007) on muuten yksi tärkeimmistä populaarimatematiikan nykyesityksistä. Suosittelen sitäkin!

Mutta asiaan.

Leikkaa oheinen kuunsirppi kahdella suoralla leikkauksella kuuteen osaan siirtämättä osia leikkausten välillä.

Ratkaisu: Näin se käy:

Opettaja H:n pulmakulma

OpettajaH.fi

Viikon helppo

Vedamatematiikkaa

Kulmanpuolittajien välinen kulma

Kadonnut euro

Ménage à quatre

Ajatustenlukutemppu

Pimeät sukat

Tuomaan talo

Tangenttikolmio

Touko-tontun toivekierros

Kuunsirppi

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon: