Väestönlaskija ja lapset

3.11.2016 | Opettaja H.

Paikkakunnalla oli menossa väestönlaskenta, ja väestönlaskija H. keräsi tietoja kätevästi ovelta ovelle kulkemalla. Eräällä ovella H. kysyi perheenisä S:ltä, kuinka monta vuotta (ei siis kuukausia, vaan täysiä vuosia) vanhoja hänen kolme lastaan olivat. Perheenisä tunnisti H:n kuuluisaksi pulmaspesialistiksi, joten hän päätti hieman kokeilla H:ta.

”Lasten ikien tulo on $36$ ja summa tuon vastapäisen talon numero”, S. vastasi pilke silmäkulmassaan. H. kävi katsomassa, mikä vastapäisen talon numero oli, ja palasi takaisin perheenisän luo. ”Olen pahoillani, mutta tarvitsen hieman lisätietoja”, H. sanoi. ”En ehdi nyt, puuro kiehuu yli ja vanhin lapsi on yläkerrassa nukkumassa”, vastasi perheenisä. ”Kiitos, mutta kyllähän tässä jo on kylliksi”, totesi lisätiedoista ilahtunut H.

Viikon helppo (no, hyvä on – helpohko) kysymys on, kuinka vanhoja lapset olivat ja mikä oli vastapäisen talon numero.

Kuva: Kathleen Conklin/Flickr (CC BY 2.0)

Ratkaisu: Luvun $36$ voi esittää seitsemällä tavalla kolmen luonnollisen luvun tulona, mutta vain kahdessa tapauksessa tulon tekijöillä on sama summa: $9+2+2=13$ ja $6+6+1=13$ . Koska vanhin lapsi nukkuu yläkerrassa, ovat lasten iät siis $9$ , $2$ ja $2$ ja vastapäisen talon numero on $13$ . (Kaksoset lasketaan siis saman ikäisiksi, vaikka teknisesti heillä varmaankin on jopa useita minuutteja ikäeroa.)

Auringonpimennys

24.10.2016 | Opettaja H.

Seuraava pulma löytyi Greg Rossin mainiolta Futility Closet -sivustolta. Ross oli puolestaan löytänyt A. Kozlovin alkuperäisen pulman venäläisestä Kvant-lehdestä. Asiaan.

H. katselee lapsensa kanssa täydellistä auringonpimennystä. Lapsi kysyy H:lta, kuinka moninkertainen auringon etäisyys maasta on verrattuna kuun etäisyyteen. H. aprikoi hetken ja muistelee, että aurinko on noin 387 kertaa kauempana maasta kuin kuu. H:n lapsi, älykäs nuorukainen, pohtii hetken ja sanoo, että sittenhän hän osaa laskea, kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna. H. sanoo lapselle, että hän on oikeassa.

Viikon helppo pulma on selvittää, kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna. Viikon vaikea pulma on laskea se ilman laskinta.

Kuva: Yutaka Tsunano/Flickr (CC BY 2.0)

Ratkaisu: Koska täydellisessä auringonpimennyksessä kuu peittää auringon melko lailla tarkalleen, voidaan ajatella ne ovat yhdenmuotoiset kappaleet. Näin olleen niiden tilavuudet ovat verrannolliset etäisyyksien kuutioon, joten auringon tilavuus on $387^3$ -kertainen kuun tilavuuteen verrattuna.

Tässä viikon helppo. Viikon hieman haastavampi pulma oli laskea luku $387^3$ ilman laskimen apua. Onnistuitko? Minä onnistuin.

Ensinnäkin $387^3=(400-13)^3$ , josta Pascalin kolmion avulla saadaan

$387^3=400^3-3\cdot 400^2\cdot 13+3\cdot 400\cdot 13^2-13^3.$

Nyt

$400^3=64000000$
$3\cdot 400^2\cdot 13=480000\cdot 13=4800000+3\cdot 480000=6240000$
$13^3=(10+3)^3=1000+900+270+27=2197$
$3\cdot 400\cdot 13^2=12\cdot 13^2\cdot 100=(2197-169)\cdot 100=202800$

Siis

$387^3=64000000-6240000+202800-2197=57960603.$

No, oliko tämän laskemisesta ilman laskinta mitään hyötyä? Ehkei, mutta sainpa ainakin itse aikani kulumaan uusintakokeita eräänä iltana koulullamme valvoessani.

Kolmion kulma

17.10.2016 | Opettaja H.

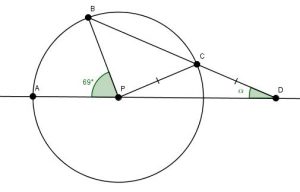
Otetaanpa välillä yksi mielenkiintoinen perusgeometrian ongelma. colingeo

Oheisessa kuvassa piste $P$ on ympyrän keskipiste ja pisteet $A, B$ ja $C$ ovat ympyrän kehän pisteitä. Piste $D$ on suorien $AP$ ja $CB$ leikkauspiste ja janat $PC$ ja $CD$ ovat yhtä pitkät. Kulman $\angle APB$ suuruus on $69^{\circ}$ . Kuinka suuri on kulma $\alpha$ ?

Ratkaisu: Kolmio $PDC$ on tasakylkinen, joten myös kulma $\angle CPD=\alpha$ . Koska kolmion yhden kulman vieruskulma on kolmion kahden muun kulman summa, saadaan $\angle PCB=2\alpha$ . Koska myös $PB$ on ympyrän säde, on kolmio $PCB$ tasakylkinen, eli $\angle PBC=2\alpha$ . Tästä edelleen vieruskulmalausetta soveltaen huomataan, että $2\alpha+2\alpha = \alpha + 69^{\circ}$ . Siis $\alpha=23^{\circ}$ .

Pöytätennispäivä

10.10.2016 | Opettaja H.

Hienoista hiljaiseloa viettänyt Pulmakulma palaa viimein syyslomalta kauniin pulman kanssa. Tämä löytyi jälleen Alex Bellosin palstalta The Guardianista.

Hannu, Kari ja Hristo viettävät koko päivän pöytätennistä pelaten. Säännöt ovat selvät: kahden pelatessa kolmas odottaa vuoroaan, voittaja jää pöydälle, häviäjä siirtyy odotusvuoroon. Päivän lopuksi he laskevat, montako peliä kukin on pelannut. Tulokset ovat seuraavat:

Hannu: 10 peliä
Kari: 15 peliä
Hristo: 17 peliä

Viikon helppo pulma on selvittää, kuka hävisi päivän toisen pelin.

Kuva: Jean-Cristophe Le Brun/Flickr (CC BY 2.0)

Ratkaisu: Koska $10+15+17=42$ ja koska jokaisessa pelissä on kaksi pelaajaa, pelasivat Hannu, Kari ja Hristo päivän aikana $21$ peliä. Kukin pelaaja on ollut mukana vähintään joka toisessa pelissä, joten riippuen siitä, onko pelaaja aloittanut peli- vai odotusvuorossa, on pelejä kerryttävä vähintään $11$ tai $10$ . Koska Hannu on pelannut vain $10$ peliä, on hän aloittanut lepovuorossa ja hävinnyt kaikki pelinsä. Toisen ottelun häviäjä on siis Hannu.

Taaperon tahdissa

12.9.2016 | Opettaja H.

H. lähti poikansa kanssa kävelylle. Oletetaan, että H. astuu kaksi askelta samassa ajassa kuin poika astuu kolme, ja oletetaan vielä, että he molemmat lähtevät liikkeelle yhtä aikaa oikealla jalalla astuen. Koska he astuvat ensimmäisen kerran yhtä aikaa vasemmalla jalalla?

Kuva: Thomas Fading/Flickr (CC BY 2.0)

Ratkaisu: Eivät milloinkaan. Kun H. ja poika astuvat seuraavan kerran yhtä aikaa, H. neljännen askeleensa ja poika kuudennen askeleensa jälkeen, he astuvat jälleen molemmat oikealla jalalla.

Tämä pulma löytyi Futility Closetista.

Saunavuoro

5.9.2016 | Opettaja H.

Tämänkertainen pulmamme on Pulmakulman ystävän Toni Vaahteran käsialaa. Kiitos, Toni!

Tuomas, Mikko, Johannes, Antti ja Kössi istuvat saunan lauteilla. Löylyttely sujuu mukavissa merkeissä kunnes löylykauha kolahtaa kiulun pohjaan. Millä keinolla saunojat voivat siltä istumalta reilusti arpoa kuka saunojista hakee vettä? Luonnollisesti älypuhelimet, nopat ja kolikot ja muut apuvälineet on jätetty pukuhuoneen puolelle.

Kuva: Wikimedia Commons (Public Domain)

Ratkaisu: Viiden hengen kivi-sakset-paperi ei oikein kuulosta hyvältä ratkaisulta. Mutta sormileikillä asia voidaan kuitenkin kätevästi ratkaista. Sovitaan, että kukin viidestä saunojasta edustaa yhtä jäännösluokkaa modulo $5$ . Eli kun kokonaislukua jaetaan viidellä, voi jakojäännös olla $0, 1, 2, 3$ tai $4$ , ja näistä jäännösluokista yksi voi edustaa kutakin saunojaa. Sitten yhtä aikaa kukin paljastaa yhdestä viiteen sormea. Sormet lasketaan yhteen ja katsotaan, mikä on jakojäännös.

Sormileikki on reilu tapa. Erilaisia sormiyhdistelmiä on $5^5=3125$ kappaletta, ja summat jakautuvat tasan kaikille viidelle jäännösluokalle, $625$ mahdollista sormisummaa kullekin. Nyt on huomattava, että jokaisen saunojan on näytettävä vähintään yksi sormi, sillä jos pelkkä nyrkkikin sallittaisiin, olisi mahdollisia yhdistelmiä $6^5=7776$ kappaletta, josta jäännösluokalle $0$ tulisi $1556$ sormisummaa, kun taas kaikille muille luokille tulisi vain $1555$ sormisummaa. Sen sijaan peli sallisi tässä tapauksessa kuudennen saunojan.¹

Olen aika pitkään ollut sitä mieltä, että jo kahden pelaajan kesken kivi-sakset-paperi on epätyydyttävä tapa arpoa. Tasapeleistä päästäisiin heti eroon pelaamalla parillista ja paritonta, jonka säännöt ovat vastaavat kuin saunapelimme. Parillisessa ja parittomassa puolestaan on ehdottomasti sallittava nollan sormen vaihtoehtokin, muutoin peli suosii paritonta. Tähän peliin törmäsin ensimmäisen kerran joskus parikymmentä vuotta sitten, mahdollisesti jossakin Hale & Pace -sarjan sketsissä, mutta varmoja muistikuvia ei ole. Joka tapauksessa olen vuosikausia pyrkinyt välttämään kivi-sakset-paperia arvontatilanteissa, mutta jotenkin parillinen ja pariton ei vain ole saavuttanut haluamaani arvostusta toveripiirissäni. Mutta ehkäpä nyt tämän saunajutun myötä…

Suunnikkaat solmussa

30.8.2016 | Opettaja H.

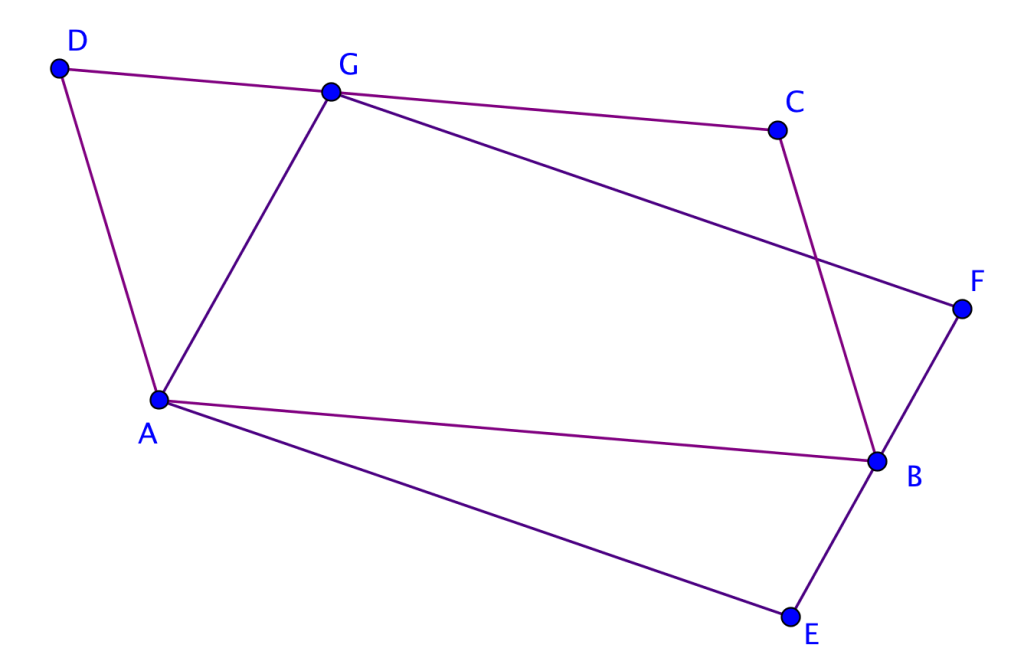suunnikaspulma Suunnikkaan $ABCD$ kärki $B$ on suunnikkaan $AEFG$ sivulla $EF$ ja suunnikkaan $AEFG$ kärki $G$ on suunnikkaan $ABCD$ sivulla $CD$ . Suunnikkaan $ABCD$ ala on $20$ . Laske suunnikkaan $AEFG$ ala.

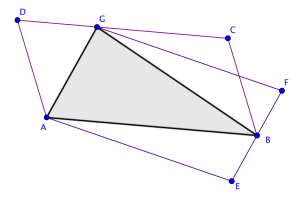Ratkaisu: suunnikaspulmaratkaisu Tutkitaan kolmiota $ABG$ . Sillä on sama kanta ja korkeus kuin suunnikkalla $ABCD$ , joten sen ala on puolet suunnikkaan alasta. Mutta toisaalta kolmiolla on sama kanta ja korkeus kuin suunnikkaalla $AEFG$ , joten sen ala on puolet myös siitä. Näin ollen suunnikkailla on pakko olla sama ala.

Sinisilmäiset tytöt

21.8.2016 | Opettaja H.

Kun vastaasi tulee kaksi Sinisalon sisarusta, on todennäköisyys sille, että molemmilla on siniset silmät, täsmälleen 50 prosenttia. Montako sisarusta Sinisalon perheessä todennäköisimmin on?

Kyllä vain, Martin Gardnerin klassisia pulmiahan tämä ilmiselvästi on.

Ratkaisu: Jos Sinisalon perheessä on $t$ tyttöä, joista sinisilmäisiä on $s$ kappaletta, on todennäköisyys kahdelle sattumanvaraiselle sinisilmälle $\displaystyle\frac{s(s-1)}{t(t-1)}$ . Tyttöjä on todennäköisimmin $4$ , joista sinisilmäisiä on $3$ , sillä seuraavat yhtälön $\displaystyle\frac{s(s-1)}{t(t-1)}=\frac{1}{2}$ toteuttavat kokonaisluvut ovat $t=21$ ja $s=15$ .

Katkaistu keppi

17.8.2016 | Opettaja H.

Keppi katkaistaan sattumanvaraisesta kohdasta. Viikon helppo pulma on, kuinka suuri osa koko kepistä lyhyempi pala keskimäärin on. Tämän ratkaistuasi voit siirtyä viikon vaikeaan pulmaan: mikä on kepin lyhyemmän ja pidemmän osan pituuksien keskimääräinen suhde?

Ratkaisu: Sattumanvarainen katkaiseminen tarkoittaa sitä, että kepin jokainen kohta on yhtä todennäköinen katkeamiskohta. Katkeamiskohta on yhtä todennäköisesti kepin puolivälin vasemmalla ja oikealla puolella. Se katkeaa keskimäärin tämän puolikkaan keskeltä, joten sen keskimääräinen pituus on $\frac{1}{4}$ koko kepin pituudesta.

Tutkitaan sitten osien pituuksien suhdetta. Yleisyydestä poikkeamatta voidaan olettaa kepin pituudeksi 1 yksikkö. Olkoon katkeamiskohta kepin loppupäässä ja olkoon pidemmän palan pituus $x$ . Lyhyempi pala on nyt siis $1-x$ ja näin ollen kysytyksi suhteeksi saadaan

$2\int_{\frac{1}{2}}^1\frac{1-x}{x} dx=2\ln 2-1\approx 0,386.$

Tämä pulma oli Frederick Mostellerin kirjasta Fifty Challenging Problems in Probability.

Kaksi tuomioistuinta

12.7.2016 | Opettaja H.

Kuvitellaan kaksi tuomioistuinta. Ensimmäisessä tuomioistuimessa istuu kolme tuomaria, joista kaksi osaa toisistaan riippumatta tehdä oikeudenmukaisen ratkaisun päätöksissään todennäköisyydellä $p$ . Kolmas tuomari heittää päätöksensä aina kolikolla. Ratkaisu saadaan enemmistöpäätöksellä. Toinen tuomioistuin koostuu vain yhdestä tuomarista, joka osaa tehdä oikean päätöksen todennäköisyydellä $p$ . Kumpi tuomioistuin antaa todennäköisemmin oikean tuomion?

Kuva: Brisan / Flickr (CC BY-NC-ND 2.0)

Ratkaisu: Molemmat tuomioistuimet ovat yhtä hyviä. Ensimmäisessä tuomioistuimessa on kolme mahdollista tapausta, joissa ratkaisu on oikeudenmukainen:

Ensimmäinen ja toinen tuomari osuvat oikeaan. Tällöin lantinheittäjätuomarin ratkaisulla ei ole väliä. Todennäköisyys tälle on riippumattomuuden nojalla $p\cdot p=p^2.$
Ensimmäinen on oikeassa, toinen väärässä ja lantinheittäjä oikeassa. Todennäköisyys tälle on $p(1-p)\cdot\frac{1}{2}=\frac{p}{2}-\frac{p^2}{2}$ .
Ensimmäinen erehtyy, toinen on oikeassa ja lantinheittäjä on oikeassa. Tämänkin todennäköisyys on $\frac{p}{2}-\frac{p^2}{2}$ .

Koska tapaukset ovat erillisiä, on tuomioistuimen onnistumistodennäköisyys näiden kolmen tapauksen todennäköisyyksien summa, eli

$p^2+\left(\frac{p}{2}-\frac{p^2}{2}\right)+\left(\frac{p}{2}-\frac{p^2}{2}\right)=p.$

Tämä pulma on Frederick Mostellerin kirjasta Fifty Challenging Problems in Probability with Solutions (Dover Publications, 1965).

Opettaja H:n pulmakulma

OpettajaH.fi

Viikon helppo

Väestönlaskija ja lapset

Auringonpimennys

Kolmion kulma

Pöytätennispäivä

Taaperon tahdissa

Saunavuoro

Suunnikkaat solmussa

Sinisilmäiset tytöt

Katkaistu keppi

Kaksi tuomioistuinta

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon: