Viikon helppo

0

Tulilanka palaa!

|

Kahdesta tulilangasta tiedetään, että kun ne sytytetään jommasta kummasta päästä, niiltä kestää palaa loppuun täsmälleen tunnin verran. Lankojen sisäinen palonopeus on täysin sattumanvarainen ja jokainen lanka on erilainen. Kuinka näiden lankojen avulla mitataan 45 minuuttia?

Kuva: Epic Fireworks / Flickr (CC BY 2.0)

Ratkaisu: Sytytä toinen lanka molemmista päistä ja toinen lanka toisesta päästä. Molemmista päistä sytytetyn langan loppuunpalamiseen kuluu 30 minuuttia. Sytytä tällöin toisenkin langan toinen pää, jolloin lanka palaa loppuun 15 minuutissa. Yhteensä paloaika on siis 45 minuuttia.

Tämä pulma tuli vastaan folj.com-sivustolla, mutta olen kyllä törmännyt siihen jossain muuallakin joskus.

0

Varjostetun alueen ala

|

Melko pitkän tauon (anteeksi, ystävät!) jälkeen Pulmakulma aktivoituu jälleen. Twitterissä tuli vastaan Mandy Wandlingin jakamana hauska kompatehtävä. Laske oheisesta kuvasta varjostetun alueen pinta-ala. Laske se sen jälkeen uudestaan.

Ratkaisu: Alhaalla olevien pienten kolmioiden alat ovat \frac{5\cdot 10}{2}=25 ja huipulla olevan kolmion ala on \frac{15\cdot 24}{2}=180. Näin ollen varjostetun alueen ala on 25+25=180=230 neliömetriä. Helppoa, eikö vain?

Ongelmia tulee siinä tapauksessa, että olettaa koko kuvion olevan tasakylkinen kolmio. Sitähän se ei ole, sillä alaosan kylkien kulmakerroin on \frac{10}{5}=2 ja huippuosan puolestaan \frac{15}{12}=\frac{5}{4}. Siispä täysin mahdollisen näköinen ratkaisu \frac{34\cdot 25}{2}-10\cdot 24=185 on ilman muuta virheellinen. Mallikuvat ovat mallikuvia!

0

Todennäköisyyksiä turnauskaaviosta

|

Pulmakulmassa järjestettiin pulmanratkontaturnajaiset. Lähes kaikki Pulmakulman tunnetut lukijat1 asetettiin turnauskaavioon, josta vain voitolla pääsee etenemään seuraavalle kierrokselle (katso esimerkki ohessa). Turnauskaavion todennäköisyysmatematiikasta saa aikaiseksi muutamia sangen mukavia pulmia. Seuraavat on poimittu Frederick Mostellerin kirjasta Fifty Challenging Problems in Probability.

Ensimmäisen kierroksen pulma on, millä todennäköisyydellä toiseksi paras ratkoja tulee kahdeksan pelaajan turnauksessa toiseksi, kun kaavion ensimmäinen kierros arvotaan.

Toisella kierroksella kysymme, millä todennäköisyydellä kaksi tiettyä pelaajaa (esim. Petri ja Toni) kohtaavat toisensa kahdeksan hengen pelaajan turnauksessa. Finaalikysymyksenä on, millä todennäköisyydellä kaksi tiettyä pelaajaa kohtaavat toisensa 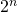2^n pelaajan turnauksessa.

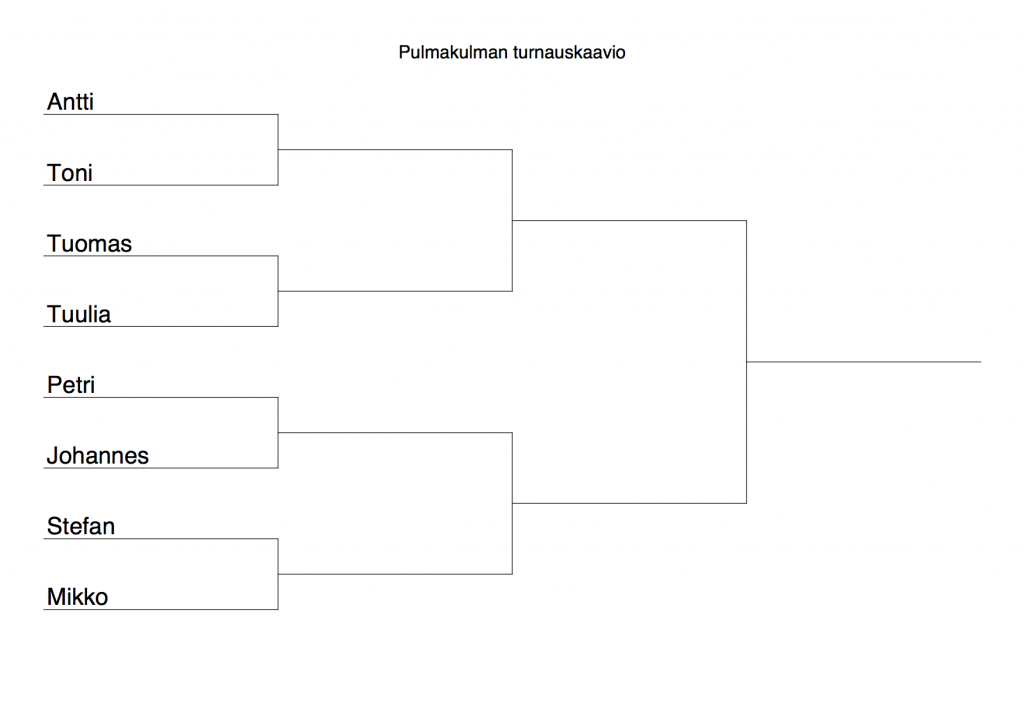
Esimerkki turnauskaaviosta (Tehty osoitteessa http://www.freebracketgenerator.com)

Ratkaisu: Ensimmäinen kysymyksistämme on helppo: jos oletetaan, että ratkojilla on pysyvä paremmuusjärjestys (eli parempi voittaa aina heikomman), tulee toiseksi paras toiseksi vain, jos ei kohtaa parasta ennen kolmatta kierrosta eli finaalia. Näin ollen toiseksi parhaan pitää olla eri puolella kaaviota. Tämän todennäköisyys on 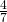\frac{4}{7}.

Toisessa ja kolmannessa kysymyksessä ei enää ole paremmuusjärjestyksellä väliä, nyt oletamme, että kummallakin otteluparin osapuolella on yhtäläiset mahdollisuudet jatkaa seuraavalle kierrokselle.

Olkoon Petri sijoitettu sattumanvaraiseen paikkaan kahdeksanpaikkaisessa kaaviossa. Nyt todennäköisyys, että Toni tulee ensimmäisessä ottelussa häntä vastaan, on 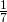\frac{1}{7}. Todennäköisyys sille, että Toni on viereisessä parissa (jolloin he kohtaisivat toisella kierroksella), on 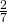\frac{2}{7}, ja todennäköisyys sille, että molemmat pääsevät toiselle kierrokselle on 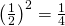\left(\frac{1}{2}\right)^2=\frac{1}{4}. Edelleen todennäköisyys sille, että Toni ja Petri ovat kaavion eri puolilla (jolloin he kohtaavat aikaisintaan finaalissa), on 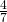\frac{4}{7}, ja todennäköisyys, että molemmat etenevät finaaliin saakka, on 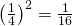\left(\frac{1}{4}\right)^2=\frac{1}{16}. Kaikkiaan Petrin ja Tonin kohtaamisen todennäköisyys on nyt

    \[\frac{1}{7}\cdot 1+\frac{2}{7}\cdot\frac{1}{4}+\frac{4}{7}\cdot\frac{1}{16}=\frac{1}{4}.\]

Ratkaistaan sitten vielä viimeinen kysymys. Jos turnauksessa on kaksi osallistujaa, kohtaavat Petri ja Toni varmasti. 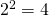2^2=4 osallistujan tapauksessa he kohtaavat todennäköisyydellä 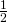\frac{1}{2}, ja äsken näytimme, että kohtaamistodennäköisyys 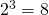2^3=8 osallistujan turnauksessa on 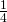\frac{1}{4}. Voimme tehdä arvauksen, että 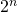2^n osallistujan turnauksessa kohtaamistodennäköisyys olisi 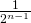\frac{1}{2^{n-1}}. Tämä voidaan osoittaa matemaattisella induktiolla.

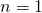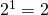Selvästi väittämämme pätee, kun n=1, eli 2^1=2 osallistujan turnauksessa Toni ja Petri kohtaavat todennäköisyydellä 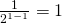\frac{1}{2^{1-1}}=1. Käytetään nyt induktio-oletuksena, että 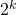2^k osallistujan turnauksessa kohtaamistodennäköisyys olisi 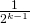\frac{1}{2^{k-1}}. On osoitettava vielä, että 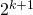2^{k+1} osallistujan turnauksessa kohtaamistodennäköisyys olisi \frac{1}{2^{(k+1)-1}}=\frac{1}{2^k}.

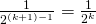Aloitetaan toteamalla, että jos osallistujia on 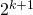2^{k+1}, ovat Petri ja Toni eri puolilla kaaviota (eli kohtaavat aikaisintaan finaalissa) todennäköisyydellä 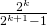\frac{2^k}{2^{k+1}-1}. Tämä on johdettavissa helposti kahdeksan pelaajan turnauksen mallinnuksen mukaisesti. Finaaliin päästäkseen Tonin ja Petrin on kummankin voitettava 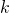k vastustajaa, minkä todennäköisyys on 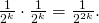\frac{1}{2^k}\cdot\frac{1}{2^k}=\frac{1}{2^{2k}}. Näin ollen todennäköisyys sille, että he ovat kaavion eri puolilla ja kohtaavat (finaalissa) on

    \[\frac{2^k}{2^{k+1}-1}\cdot\frac{1}{2^{2k}}.\]

Todennäköisyys sille, että Toni ja Petri ovat samalla puolella kaaviota, eli kohtaamassa ennen finaalia on 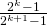\frac{2^k-1}{2^{k+1}-1}. Induktio-oletuksen mukaan heidän todennäköisyytensä kohdata tässä 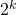2^k osallistujan (ali-)turnauksessa on 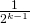\frac{1}{2^{k-1}}. Näin ollen yhteenlasketuksi kohtaamistodennäköisyydeksi 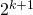2^{k+1} osallistujan turnauksessa saadaan

    \[\frac{2^k-1}{2^{k+1}-1}\cdot\frac{1}{2^{k-1}}+\frac{2^k}{2^{k+1}-1}\cdot\frac{1}{2^{2k}},\]

joka toden totta sievenee muotoon

\frac{1}{2^k}.

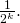
Näin ollen induktioväite on osoitettu todeksi ja samoin koko väittämä.

0

Ruuhkavuodet

|

Olen ilokseni kuullut, että Pulmakulmalla on ystäviä myös etelässä. Tämä seuraava pulma on saatu fanifiktiona, ja koska se perustunee tositapahtumiin, suojeltakoon lähdettä ainakin vähän.

No niin. Stefanilla on kolme lasta. Lasten kanssa kävellään päiväkodin ja koulun väliä viitenä päivänä viikossa. Lapsi A kiukuttelee keskimäärin 1/5 matkoista, lapsi B 3/5 matkoista ja lapsi C 4/5 matkoista. Mikä on todennäköisyys, että viikossa olisi edes yksi päivä, jolloin kukaan lapsista ei kiukuttele?

Ratkaisu: Ratkaistaan ongelma käyttämällä yleistä kertolaskusääntöä, komplementtisääntöä sekä binomitodennäköisyyttä. Tilannehan voidaan tulkita toistokokeeksi, jossa toistetaan yhden päivän käyttäytymistä viisi kertaa.

Oletetaan, että lasten kiukuttelualttiudet ovat toisistaan riippumattomia. Näin ollen yhteen suuntaan todennäköisyys sille, että kukaan ei kiukuttele on

    \[\frac{4}{5}\cdot\frac{2}{5}\cdot\frac{1}{5}=\frac{8}{125}.\]

Päivässä kuljetaan kaksi matkaa, joten todennäköisyys sille, että kukaan ei kiukuttele yksittäisenä päivänä on

    \[\left(\frac{8}{125}\right)^2=0,00496.\]

Siis todennäköisyys sille, että ainakin joku kiukuttelee yksittäisenä päivänä on 1-0,004096=0,995904.

No, ei tilanne ole kuitenkaan ihan näin synkkä, sillä viikossa päiviä on viisi. Voidaan ajatella päivien toistuvan aina samanlaisina (eli toistot ovat toisistaan riippumattomia), jolloin binomitodennäköisyyttä hyödyntäen voidaan laskea todennäköisyys sille, että ainakin yhtenä päivänä kukaan ei kiukuttele. Siis P(\mbox{ainakin kerta ilman kiukkua})=1-P(\mbox{joku kiukuttelee aina}), eli

    \[1-0,995904^5=0,02031\ldots\approx2,0\%.\]

0

Kissat ja hiiret

|

Viisi kissaa saa kiinni viisi hiirtä viidessä minuutissa. Montako kissaa tarvitaan nappaamaan sata hiirtä sadassa minuutissa?

Kuva: Volodymyr Pavlyuk / Flickr (CC BY-NC-ND 2.0)

Ratkaisu: Viisi kissaa riittää.

1

Nimekäs lapsi

|

Herra H. tapasi kadulla entisen luokkatoverinsa, joka työnsi lastenvaunuja. He eivät olleet kohdanneet kertaakaan miltei 20 vuoteen. He kertoilivat kuulumisia tovin. Luokkatoveri oli oleskellut lähinnä Saksassa ja hänellä oli saksalainen puolisokin. H. kysyi, mikä oli heidän pienen tyttärensä nimi. Toveri kertoi heidän nimenneen tytön äitinsä mukaan. ”Hei, Laura!” H. sanoi vaunussa hymyilevälle tyttöselle. Miten H. tiesi hänen nimensä, vaikka ei tuntenut luokkatoverin puolisoa?

Ratkaisu: H:n luokkatoverin nimi oli Laura, joten tytönkin nimi oli Laura.

0

Rautakaupassa

|
Kuva: Wikimedia Commons

Kuva: Wikimedia Commons

Olet ostoksilla rautakaupassa. Myyjä sanoo, että 1 maksaa 50 senttiä, 12 maksaa euron ja 144 maksaa 1,50 euroa. Mitä olet ostamassa?

Ratkaisu: Olet ostamassa numeroita esimerkiksi virsitauluun tai talon seinään. Martin Gardner hallitsi myös nämä pienet kompatehtävät.

0

Hitsattu kuutio

|

H. hankki metallitankoa, koska hänen oli tarkoitus tehdä kuution muotoinen kehikko. Hän ajatteli pätkiä tangon 12 yhtä pitkäksi palaksi ja sitten hitsata ne yhteen. Aina näppärä Tapsa kysyi, eikö tanko kannattaisi katkoa hieman pidemmiksi paloiksi ja taivutella palat suoriin kulmiin, jotta ihan niin montaa hitsauspistettä ei tarvittaisi.

Viikon helppo kysymys on, kuinka monesta kohdasta tällainen pidemmistä paloista vääntelemällä tehty kehikko vähimmillään tarvitsee hitsata.

Ratkaisu: Kuution jokaisessa kärjessä kohtaa kolme särmää, joten vaikka tankoa kuinka vääntelisi, on kuutio hitsattava kaikista kahdeksasta kärjestä.

2

Ohittelua

|

Juostaanpa kilpaa! Ollaan loppukirivaiheessa. Pari kiperää kysymystä:

  1. Ohitat toisena juoksevan. Monentenako olet nyt?
  2. Ohitat viimeisenä juoksevan. Monentenako olet nyt?
Perspektivet Museum/Flickr (CC BY-NC-ND 2.0)

Kuva: Perspektivet Museum/Flickr (CC BY-NC-ND 2.0)

Ratkaisu: Näin helpossa kysymyksessä aivot meinaavat mennä ensin solmuun. Vastasitko ensin jompaan kumpaan kysymykseen väärin? Tunnusta vaikka kommenttikenttään. Toisena juoksevan ohitettuasi olet toisena, viimeistä et voi ohittaa!

Tämä mainio viikon vitsi löytyi loistavaksi pulmailulähteeksi osoittautuneesta Alex Bellosin Can You Solve My Problems -opuksesta.

0

Hullut Hattuset

|

Villellä, Miihkalilla ja Leolla on laatikossa viisi hattua: kaksi keltaista ja kolme punaista. He ottavat silmät kiinni laatikosta yhden hatun päähänsä ja sulkevat sen jälkeen laatikon. He eivät näe omaa hattuaan eivätkä laatikkoon jääneitä hattuja, mutta toistensa hatut he näkevät. Käydään seuraava keskustelu:

Leo: ”En tiedä hattuni väriä.”
Miihkali: ”En tiedä hattuni väriä.”
Ville (joka näkee kaksi punaista hattua): ”Tiedän hattuni värin!”

Minkä värinen hattu Villellä on?

Kuva: Tomi Palsa /Hattuset.net

Kuva: Tomi Palsa/Hattuset.net

Ratkaisu: Leo voisi tietää hattunsa värin ainoastaan, jos hän näkisi kaksi keltaista hattua. Miihkali tietää tämän, joten hän tietää, että Leo näki korkeintaan yhden keltaisen hatun. Leon hatun Miihkali näkee punaiseksi, joten keltainen hattu voi olla joko Miihkalin tai Villen päässä. Jos Villen hattu olisi keltainen, voisi Miihkali päätellä oman hattunsa punaiseksi, mutta koska hän ei näin voi tehdä, on Villelläkin pakko olla punainen hattu.