Viikon helppo

4

Kaksoset

|

Oili ja Olli ovat kaksoset. Vähän aikaa sitten olin Ollin syntymäpäivillä. Kaksi päivää myöhemmin olin hänen isosiskonsa Oilin syntymäpäivillä. Miten tämä on mahdollista?

Kuva: John Tenniel (Wikimedia Commons)
Ratkaisu: Oili ja Olli ovat syntyneet Tyynenmeren yllä mannertenvälisellä lennolla Aasiasta Amerikkaan. Kun Oili syntyi, oli 1. maaliskuuta. Kun Olli syntyi hieman myöhemmin, lentokone oli juuri ylittänyt kansainvälisen päivämäärärajan, jonka itäpuolella oli yhä 28. helmikuuta. Synttärijuhlista on tarkemmin muisteltuna aikaa jo reilut kolme vuotta, sillä kahden päivän ero saadaan tietenkin karkausvuosina.
 
Tämä pulma marssi vastaan Alex Bellosin pulmapalstalta The Guardianista.

0

Ei ihan suorakulmainen kolmio

|

Suhteellisen pitkän tauon jälkeen on uuden pulman aika. Tämä pulma tuli (vähän eri muodossa) vastaan Presh Talwalkarin Mind Your Decisions -kanavalla YouTubessa.

Suorakulmaisen kolmion hypotenuusa on 10 ja hypotenuusalle piirretty korkeusjana on 6. Miksei kolmion ala ole 30?

Ratkaisu: Suorakulmaisia kolmioita, joiden hypotenuusa on 10, on useita. Koska samaa kaarta vastaava kehäkulma on puolet keskuskulmasta, voidaan kaikki tällaiset kolmiot muodostaa siten, että suoran kulman kärki valitaan puoliympyrältä, jonka halkaisija on 10. Tällöin puoliympyrän säde on 5, mikä on myös suurin mahdollinen korkeusjanan pituus. Siis tehtävänannon mukaista kolmiota ei voi olla edes olemassa!

0

Liikenneympyrä

|

Eipä olekaan hetkeen tullut käännetyksi Alex Bellosin pulmia, joten eiköhän liene korkea aika ottaa hänen tehtävälaaristaan yksi näppärä looginen ongelma. Bellos on saanut seuraavan pulman Pippa Suttonilta.

Adrian, Bruce, Clive, Dave ja Eddie ajavat ympyrää polkuautoilla, joiden rekisterinumerot ovat 1, 2, 3, 4 ja 5 (muttei välttämättä tässä järjestyksessä). He näkevät välittömästi edellään ja välittömästi takanaan ajavien rekisterinumerot, mutteivät omaansa. Lisäksi he kaikki ovat täydellisiä loogikkoja. He kuulevat kysymyksen:

”Ajatko autolla, jonka rekisterinumero on jonkin kokonaisluvun neliö?”

”En tiedä!” kuuluu vastaus kuin yhdestä suusta.

”Ajatko autolla, jonka rekisterinumero on jonkin kokonaisluvun neliö?” kuuluu kysymys uudestaan.

”En tiedä!” kaikki vastaavat, paitsi Eddie, joka vastaa ”En aja”.

Seuraavaksi ääni kysyy: ”Onko rekisterinumerosi suurempi kuin takanasi ajavalla?”

Dave huutaa, ettei tiedä. Tämän jälkeen Bruce ja Eddie sanovat, että ei ole, ja Adrian ja Clive toteavat, että on.

Mitkä ovat Adrianin, Brucen, Cliven, Daven ja Eddien rekisterinumerot?

Kuva: Tom/Flickr (CC BY 2.0)

Ratkaisu: Neliöitä rekisterinumeroista ovat 1 ja 4. Kukaan ei tietenkään voi tietää, ajaako itse neliönumeroisella autolla, mutta jos joku näkisi sekä edessään että takanaan neliön, voisi hän päätellä, että hän ei aja neliönumeroisella autolla. Ensimmäisellä kysymyksellä selviää, että kukaan ei näe kahta neliötä. Toisella kysymyksellä Eddie on onnistunut päättelemään, että koska kukaan ei näe kahta neliötä, eikä hän näe yhtään, että hänen autonsa ei ole neliönumeroinen. Eddien ilmoituksesta tiedetään myös heti, että autot 1 ja 4 kuuluvat Brucelle ja Clivelle, mutta järjestys ei vielä ole selvä.

Koska Dave ei tiedä, ajaako hänen takanaan häntä suurempi vai pienempi rekisteri, ei Cliven rekisteri voi olla 1. Siis Cliven rekisteri on 4 ja Brucen rekisteri on 1. Koska Eddie tietää, että hänen rekisterinsä on suurempi kuin Daven, ja koska Adrianin rekisteri on suurempi kuin Eddien, on Daven rekisteri 2, Eddien 3 ja Adrianin 5.

0

Numerot järjestykseen

|

Kahdeksannumeroisessa luvussa on kaksi ykköstä, kaksi kakkosta, kaksi kolmosta ja kaksi nelosta. Ykköset ovat yhden numeron päässä toisistaan, kakkoset kahden numeron, kolmoset kolmen numeron ja neloset neljän numeron päässä toisistaan. Mikä luku on kyseessä?

Ratkaisu: Luku on 41312432 tai tämän peilikuva 23421314. Tämän pulman lähde on Futility Closet.

 

0

Pillinvääntöä

|

Taitetaan mehupilli kahdesta sattumanvaraisesta kohdasta. Millä todennäköisyydellä taitoksista saadaan kolmio?

Kuva: Petter Duvander/Flickr (CC BY-NC 2.0)

Ratkaisu: Kolmioepäyhtälön mukaan kolmio syntyy, mikäli yksikään paloista ei ole pidempi kuin kahden muun summa. Jos sovitaan, että pillin pituus on 1, tämä tarkoittaa sitä, että kunkin kolmesta osasta pitää olla lyhyempi kuin \frac{1}{2}.

Sovitaan, että taitoskohdat ovat x ja y, missä 0<x<1 ja 0<y<1. Kolmio muodostuu jommalla kummalla seuraavista ehdoista:

  1. x<y; x<\frac{1}{2}; y-x<\frac{1}{2}; 1-y<\frac{1}{2} tai
  2. y<x; y<\frac{1}{2}; x-y<\frac{1}{2}; 1-x<\frac{1}{2}.

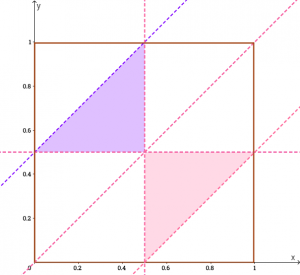Oheisessa kuvassa on ensimmäisen ehdon ratkaisualue on sinertävänä ja jälkimmäisen ehdon ratkaisualue vaaleanpunaisena. Kumpikin näistä on kooltaan \frac{1}{8} koko neliöstä, joten kolmio muodostuu todennäköisyydellä \frac{1}{4}.

Tämän pulman lähde on Matthew Scroggsin pulmasivu.

0

Neliöiden naapurit

|

 

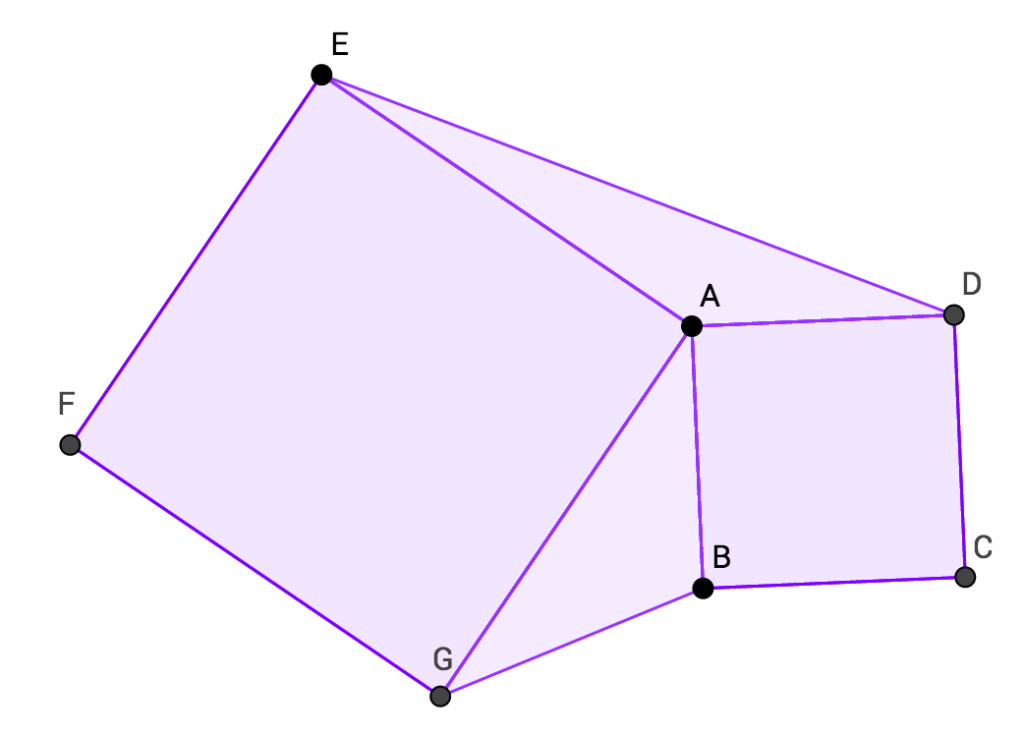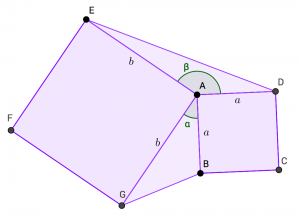
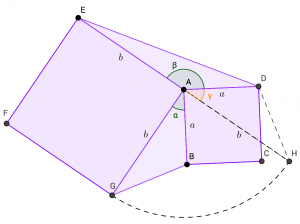
Nyt on vuorossa perusgeometriaa! Oheisessa kuvassa ABCD ja AEFG ovat neliöitä. Osoita, että kolmioilla AGB ja ADE on sama pinta-ala.

Tämä pulma on Daniel Grillerin kirjasta Elastic Numbers. Löysin siihen helpon, mutta melko tylsän ratkaisun, joka on perusteltavissa lukiogeometrialla. Grillerin oma ratkaisu puolestaan on oleellisesti yksinkertaisempi ja kauniimpi. Sen ymmärtää alakoululainenkin! Siksipä tässä on sangen nätti viikon helppo pulma.

Kuva 1: Suplementtikulmat

Ratkaisu: Oma ideani perustui siihen, että koska kulmat BAD ja EAG ovat suoria, ovat kulmat \alpha ja \beta ovat suplementtikulmia, eli ne muodostavat yhdessä 180^{\circ} kulman (kuva 1). Lukiotrigonometriassa opimme rakkaan työkalumme yksikköympyrän avulla, että kulmalla ja sen suplementtikulmalla on sama sini. Ja koska kolmion ABG ala voidaan laskea kaavalla \displaystyle\frac{1}{2}ab\sin \alpha, missä a ja b ovat kulman \alpha kyljet, ja yhtä lailla kolmion ADE ala on \displaystyle\frac{1}{2}ab\sin \beta, niin selvästi kolmioiden alat ovat samat.

Joo, ei hirveän tyylikäs ratkaisu, mutta ratkaisu kuitenkin, ja itse tuloshan on varsin mukava.

Kuva 2: Kierto pisteen A ympäri

Daniel Griller lähtee myös samasta ajatuksesta: \alpha+\beta=180^{\circ}. Mutta hän vie idean nokkelasti pidemmälle (Kuva 2). Koska AB=AD=a, voidaan kolmio AGB kiertää 90 astetta pisteen A ympäri kolmioksi AHD, jossa AH=AG=b ja \gamma=\alpha (ja siis samalla \gamma+\beta=180^{\circ}, joten pisteet A, E ja H ovat samalla suoralla). Nyt meillä on kaksi kolmiota, AHD ja AED, joilla on sama kanta b ja sama korkeus, mistä ratkaisu välittömästi seuraa.

0

Istumapaikka

|

Kuva: Rob Stanley/Flickr (CC BY-NC 2.0)

Mikko istuu suuressa loppuunmyydyssä suorakulmion muotoisessa katsomossa1. Hänen edessään olevilla riveillä istuu 175 henkeä ja takanaan olevilla riveillä 400 henkeä. Sarakkeissa Mikon vasemmalla puolella istuu 312 henkeä ja oikealla puolella 264 henkeä. Monennenko rivin monennellako paikalla Mikko istuu?

Ratkaisu: Pulman ratkaisu piilee jaollisuudessa. Aloitetaan tutkimalla Mikon edessä olevia 175 paikkaa. Nyt luvun 175 alkutekijähajotelma on 175=5^2\cdot 7, joten järkeviä mahdollisuuksia Mikon eteen ovat vain 7 riviä, joilla on 25 paikkaa kullakin, tai 5 riviä, joilla on 35 paikkaa, tai toisinpäin.

Mikon takana tilanne on hieman monimutkaisempi: alkutekijähajotelmaksi saadaan 400=2^4\cdot 5^2, mutta koska 35 ei ole luvun 400 tekijä, jää parhaaksi vaihtoehdoksi, että Mikon takana olisi 16\cdot 25 paikkaa.

Tarkastellaan sitten sivuja. Nyt 312=2^3\cdot 3\cdot 13 ja 264=2^3\cdot 3\cdot 11. Näistä hyvät paikkamääräkombinaatiot ovat 13\cdot 24=312 ja 11\cdot 24=264.

Yhdessä näistä voidaan päätellä, että salissa pitäisi olla 24 riviä ja 25 saraketta, ja edelleen Mikon paikka on 8. rivillä, 14. sarakkeessa.

Voidaan myös helposti huomata, että jos lasketaan Mikon edestä ja takaa löytyvät paikat yhteen, saadaan 175+400=575 paikkaa lukuunottamatta riviä, jolla Mikko istuu, ja sivuilta laskien 312+264=576 paikkaa lukuunottamatta saraketta, jossa Mikko istuu. Näin ollen sarakkeita on oltava yksi enemmän kuin rivejä.

Tämä pulma on peräisin Daniel Grillerin uudesta kirjasta Elastic Numbers, jota ovat suitsuttaneet ainakin Alex Bellos ja Matthew Scroggs – molemmat miehiä, joiden pulmasuosituksiin kannattaa tarttua. Niinpä kyseinen opus koristaakin työpöytääni toivottavasti jo tulevalla viikolla!

0

Funikulaari

|

Ystäväpiirissäni on useita, joiden mielestä funikulaari eli kiskoköysirata on yleensä vierailemisen arvoinen kohde, mikäli matkalla sellainen vastaan sattuu. Perusideahan on, että funikulaarissa on kaksi vaunua, joista toisen matkatessa ylös toinen tulee samaan aikaan alas. Jännimmissä funikulaareissa on vain yksi raide paitsi radan puolessavälissä, jossa vaunujen ohituspaikkaan on tehty pieni pätkä kaksiraiteista rataa. Mutta asiaan.

Kössi oli reissussa ja osui erityisen pitkän funikulaarin luo. Yhdensuuntainen matka-aika radalla oli peräti 15 minuuttia. Kössi lähti jalkapatikassa ala-asemalta kipuamaan kohti yläasemaa samaan aikaan kun vaunu lähti liikkeelle1. Kössi oli selvästi hitaampi kuin funikulaari. Vastaantuleva vaunu ohitti Kössin 12,5 minuutin kuluttua liikkeellelähdön jälkeen. Viikon helpot kysymykset ovat, koska jompi kumpi vaunu ohittaa Kössin seuraavan kerran ja kumpaan suuntaan vaunu on silloin menossa. (Oletetaan tehtävän vuoksi, että vaunut lähtevät ylä- ja ala-asemilta liikkeelle välittömästi sinne päästyään. Oletetaan myös, että sekä vaunut että Kössi liikkuvat tasaisella nopeudella.)

Kuva: Mark Fischer/Flickr (CC BY-SA 2.0)

Ratkaisu: Tämä pulma on versioitu Lewis Carrollin teoksessa A Tangled Tale (1885) olleesta ongelmasta.

Koska kohtaaminen tapahtuu 12 ja puolen minuutin jälkeen, on funikulaarin nopeus viisinkertainen Kössin nopeuteen verrattuna. Lasketaan ensin, koska tämä vastaantuleva vaunu ohittaa Kössin seuraavan kerran, ja todetaan sitten, että yläasemalta tuleva vaunu ei vielä silloin ole tullut vastaan.

Olkoon funikulaariradan koko pituus a ja olkoon kohta, jossa Kössi ja alhaalta tuleva vaunu kohtaavat seuraavan kerran, etäisyydellä b ala-asemalta. Olkoon t ajanhetki, jolloin kohtaaminen tapahtuu. Merkitään nyt Kössin nopeutta v_k=\frac{b}{t} ja funikulaarin nopeutta v_f=\frac{a+b}{t}. Funikulaari kulkee siis ensin koko radan ja sitten vielä matkan b rinnettä ylöspäin. Koska funikulaarin nopeus on viisinkertainen, saadaan yhtälö

    \[\frac{a+b}{t}=5\cdot\frac{b}{t},\]

josta t pois kertomalla saadaan, että

    \[b=\frac{1}{4}a.\]

Tästä voidaan päätellä, että kohtaaminen tapahtuu, kun aikaa on tarkastelun alusta kulunut koko radan kesto eli 15 minuuttia sekä neljäsosa noususta, eli 3 minuuttia ja 45 sekuntia. Näin ollen ensimmäisestä sivuutuksesta toiseen kuluu tämä 3 minuuttia ja 45 sekuntia sekä 2 ja puoli minuuttia, joka oli jäljellä ensimmäisestä radan mitasta. Siis yhteensä aikaa kuluu 6 minuuttia ja 15 sekuntia.

Koska seuraava kohtaaminen tapahtuu ennen radan puoltaväliä, on Kössin ohittava vaunu tulossa ala-asemalta.

0

Kissa kiinnostaa

|

Hieman olen miettinyt, kuinka paljon vielä kehtaan tänne Alex Bellosin loistavaa The Guardianin pulmapalstaa suomentaa, mutta menköön nyt vielä ainakin tämän kerran. Voi kai tätä jonkinlaisena toimituksellisena työnä sentään pitää. Tämänkertainen pulma on mukaelma muutaman vuoden takaa The New York Timesissa julkaistusta ”prinsessapulmasta”. Ja tässä se tulee.

Käytävällä on ovia rivissä, ja yhden oven takaa löytyy kissa. Kissa! Sinun tehtäväsi on löytää kyseinen luomakunnan kruunu. Mutta säännöt ovat vaativat: saat arvata vain kerran, jonka jälkeen kissa siirtyy (näennäisen!) sattumanvaraisesti yhden oven joko oikealle tai vasemmalle.

Viikon helppo pulma on löytää kissa korkeintaan neljännellä arvauksella, kun ovia on rivissä neljä.

Viikon vaikea pulma on selvästi haastavampi: mikä on pienin määrä arvauksia, joilla löydät kissan varmasti, kun kissa piileskelee seitsemän oven takana?

Selvennyksiksi vielä todettakoon, että kissa siirtyy jokaisen arvauksen jälkeen, ja että ovet ovat tosiaankin rivissä, eli vasemmanpuolimmainen ja oikeanpuolimmainen ovi ovat käytävän reunoilla, eikä niistä ole yhteyttä toisiinsa ”nurkan ympäri”.

Kuva: Abby Rosenberg / Flickr (CC BY-NC 2.0)

Ratkaisu: Tämä pulma on erinomainen esimerkki eräästä matemaattisesta ongelmanratkaisumenetelmästä, jossa monimutkaista pulmaa lähestytään ennen yksinkertaisemman erikoistapauksen kautta ja sitten pyritään löytämään menetelmä, joka sopii myös monimutkaisemmille tapauksille. Ajatellaanpa vaikka tätä pulmaa yksinkertaisimmillaan. Jos ovia olisikin vain yksi, olisi kissa varmasti sen takana. Jos taas ovia olisi kaksi, niin ellei kissa heti olisi arvatun oven takana, siirtyisi se sinne seuraavaksi kerraksi. Oikeastaan kolmen oven versio on ensimmäinen mielekäs vaihe, jossa yksi pulman lopulliselle ratkaisemiselle keskeinen idea tulee ensimmäistä kertaa esiin: jos kissa ei ole keskioven takana, on sen oltava reunassa, josta se siirtyy keskioven taakse seuraavalle kierrokselle. Kissa ei siis voi olla kahta kertaa peräkkäin reunaoven takana.

Tehdään nyt ratkaisuista kaaviokuvat. Merkitään avattua ovea A:lla ja mahdollista kissan paikkaa K:lla. Esittelen tässä nyt pisimmät tiet – kissahan voisi hyvällä onnella tulla vastaan jo aiemminkin. Mutta seuraavat reitit johtavat varmasti ratkaisuun. Neljän oven ratkaisualgoritmi on seuraava:

    \[\begin{array}{|c|c|c|c|}K&A&K&K\\ \hline&K&A&K\\ \hline K&&A&\\ \hline &A&&\end{array}\]

Pienellä pohdinnalla ratkaisumalli alkaa hahmottua. Muutamia huomioita voi tehdä nopeasti. Ei kannata aloittaa reunalta, se ei johda mihinkään. Jos kissa on reunalla, ei se voi seuraavalla kerralla siellä olla. Jos tästä laajennetaan viiden oven tapaukseen, huomataan myös se, että keskimmäisestä ovesta aloittaminen ei myöskään toimi. Miten voidaan alkaa rajoittaa kissan paikkoja? Voidaanko osa ovista rajata pysyvästi kissavapaaksi alueeksi?

Itse painin aika tovin viiden oven ongelman kanssa, mutta sitten juttu alkoi aueta. Sen innoittamana kuuden oven versio ratkesi nopeasti, eikä seitsemän ovea ollut sitten enää sen kummempi haaste. Alex Bellosin linkkaaman alkuperäisen pulman ovien lukumäärä oli 17, mutta sama ratkaisualgoritmi toimii siihenkin. Jos ovia on k kappaletta, arvauksia tarvitaan aina korkeintaan 2k-4. Tässä ratkaisu seitsemälle ovelle. Arvauksia tarvitaan korkeintaan kymmenen. En selitä enempää. Tutki itse (ja tule vasta sitten tarkistamaan ratkaisu)!

    \[\begin{array}{|c|c|c|c|c|c|c|}K&A&K&K&K&K&K\\ \hline &K&A&K&K&K&K\\ \hline K&&K&A&K&K&K\\ \hline &K&&K&A&K&K\\ \hline K&&K&&K&A&K\\ \hline&K&&K&&A&\\ \hline K&&K&&A&&\\ \hline &K&&A&&&\\ \hline K&&A&&&&\\ \hline &A&&&&&\end{array}\]

0

Keskinopea auto

|

H. haluaisi ajaa kahden kilometrin matkan 60 km/h keskinopeudella. Tietyön takia ensimmäinen kilometri sujuu kuitenkin vain keskinopeudella 30 km/h. Kuinka lujaa H:n pitää ajaa loppumatka?

Kuva: William Creswell / Flickr (CC BY 2.0)

Ratkaisu: Kyllä vain, tämä oli kompa. Jos H. haluaa ajaa kaksi kilometriä keskinopeudella 60 km/h, on hänellä aikaa siihen kaksi minuuttia. Kuitenkin nopeudella 30 km/h kilometrin kulkeminen kestää juuri mainitun kaksi minuuttia, joten aika on jo käytetty, kun vauhtia voitaisiin kiihdyttää. H. ei siis pysty ajamaan kahta kilometriä kahdessa minuutissa mitenkään.