Varsinkin suurilla ulkomaisilla lentoasemilla ja metroasemilla on käytössä liukukäytäviä siirtymien helpottamiseksi. Olenkin miettinyt, miksi näitä henkilökuljettimia oikein kutsutaan, ja ilmeisesti juuri liukukäytävä on virallinen suomenkielinen nimitys. Englanniksi vekottimella on hauskemmalta kalskahtava nimitys, travelator.
Mutta asiaan. Matematiikan arvostetuimmalla palkinnolla, Fieldsin mitalilla, vuonna 2006 palkittu australialaismatemaatikko Terence Tao on esittänyt seuraavan pulman:
Matkalla turvatarkastuksesta portille on sekä tavallista lattiaa että liukukäytäviä. Lattialla H. kävelee nopeudella ![]() ja liukukäytävä liikkuu nopeudella
ja liukukäytävä liikkuu nopeudella ![]() (jolloin H. voi halutessaan siis edetä liukukäytävällä nopeudella
(jolloin H. voi halutessaan siis edetä liukukäytävällä nopeudella ![]() ). H:n täytyy pysähtyä matkalla solmimaan kengännauhansa, johon kuluu tietty vakioaika. Jos portille pitää päästä mahdollisimman nopeasti, kannattaako kengännauhat solmia lattialla, liukukäytävällä vai onko sillä mitään väliä?
). H:n täytyy pysähtyä matkalla solmimaan kengännauhansa, johon kuluu tietty vakioaika. Jos portille pitää päästä mahdollisimman nopeasti, kannattaako kengännauhat solmia lattialla, liukukäytävällä vai onko sillä mitään väliä?
Ratkaisu: Nauhat kannattaa solmia liukukäytävällä. Pulma voidaan ratkaista tietysti täysin matemaattisesti nopeuden, matkan ja ajan yhdistävää yhtälöä ![]() hyödyntäen. Ei kuitenkaan mennä nyt ihan yksityiskohtiin, vaan tyydytään Alex Bellosin hienoon havainnollistukseen.
hyödyntäen. Ei kuitenkaan mennä nyt ihan yksityiskohtiin, vaan tyydytään Alex Bellosin hienoon havainnollistukseen.
Oletetaan, että matkalla turvatarkastuksesta portille on ensin vain lattiaa ja sitten vain liukukäytävää. Sovitaan, että H. ja S. lähtevät yhtä aikaa kävelemään samalla nopeudella turvatarkastuksesta. Juuri ennen liukukäytävän alkua S. ryhtyy solmimaan kengännauhojaan. H. astuu vielä askeleen ja alkaa solmia nauhojaan liukukäytävän päällä. He ovat valmiit kenkiensä kanssa oleellisesti samaan aikaan, jonka jälkeen he jatkavat samalla nopeudella pitkin liukukäytävää. H. on kuitenkin ehättänyt jo edelle, eikä S. voi enää saada häntä kiinni.



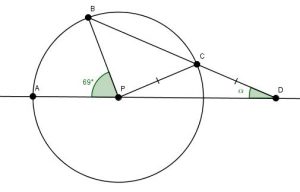




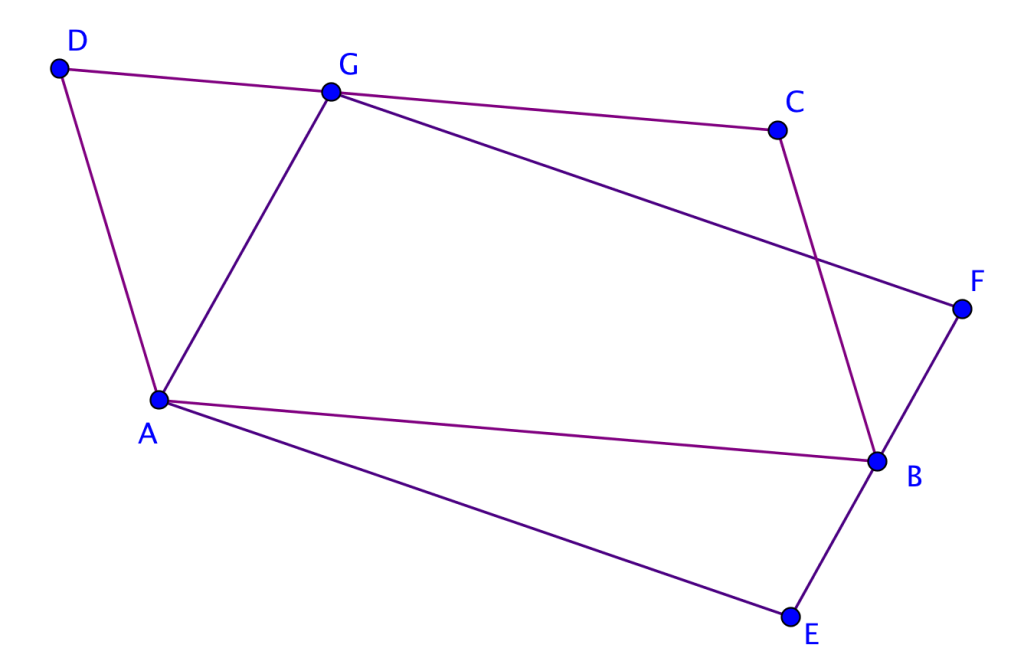 Suunnikkaan
Suunnikkaan 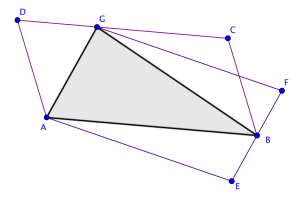 Tutkitaan kolmiota
Tutkitaan kolmiota 