Pulmat

0

Puuttuva numero

|

Colin Beveridge (suuri suomalaisten ystävä, muuten!1) esitti blogissaan hauskan lukuongelman. Seitsemännumeroinen luku on kuuden peräkkäisen parillisen luvun tulo. Tiedetään, että sen kuusi viimeistä numeroa ovat 870720. Mikä on luvun ensimmäinen numero?

Ratkaisu: Kuten Colin Beveridgekin toteaa, olisi ratkaisu raa’alla voimalla, esim. ohjelmoimalla, tylsää. Tehdään jotain hauskempaa.

Kuuden peräkkäisen parillisen luvun tulo voidaan ilmoittaa muodossa

    \[2n\cdot 2(n+1)\cdot 2(n+2)\cdot 2(n+3)\cdot 2(n+4)\cdot 2(n+5).\]

Tekijöinä ovat siis 2^6 ja kuusi peräkkäistä kokonaislukua, n, n+1, n+2, n+3, n+4 ja n+5. Kuudesta peräkkäisestä luvusta täsmälleen kaksi on kolmella jaollisia, joten koko tulon on oltava yhdeksällä jaollinen. Edelleen luku on yhdeksällä jaollinen vain, jos sen numeroiden summa on yhdeksällä jaollinen. Ja koska 8+7+0+7+2+0=24, on puuttuvan numeron oltava 3. Kysytty luku voi siis olla vain 3870720.

Varmistetaan vielä, että tämä luku todella on kuuden peräkkäisen parillisen luvun tulo. Koska 2^6 on tekijä, saadaan tällä jakamalla 60480, jonka pitäisi nyt siis olla kuuden peräkkäisen luvun tulo. Jaetaan alkutekijöihin:

    \[60480=2^6\cdot 3^3\cdot 5\cdot 7\]

.

Nyt on melko suoraviivaista alkaa päätellä tulon tekijöitä tästä. Koska 60480<10^6, eivät ainakaan kaikki tulon tekijät voi olla suurempia kuin 10. Alkutekijähajotelmasta puuttuu luku 11, joten tulon kaikkien tekijöiden on nyt itse asiassa välttämättä oltava tätä pienempiä.

Kuudesta peräkkäisestä luvusta aina täsmälleen kaksi on jaollisia kolmella, ja korkeintaan yksi yhdeksällä. Jotta 3^3 tulisi käytetyksi alkutekijähajotelmasta, on 9 välttämättä yksi tekijöistä. Toisen kolmella jaollisen tekijän on tällöin oltava 6. Koska kyse oli peräkkäisistä luvuista, myös 7 ja 8 ovat tekijöitä. Tämä jättää alkutekijöihin enää 2^2\cdot 5, eli peräkkäisten lukujen tulo on 4\cdot 5\cdot 6\cdot 7\cdot 8\cdot 9=60480. Siis edelleen

    \[$8\cdot 10\cdot 12\cdot 14\cdot 16\cdot 18=3870720.\]

4

Kaksoset

|

Oili ja Olli ovat kaksoset. Vähän aikaa sitten olin Ollin syntymäpäivillä. Kaksi päivää myöhemmin olin hänen isosiskonsa Oilin syntymäpäivillä. Miten tämä on mahdollista?

Kuva: John Tenniel (Wikimedia Commons)
Ratkaisu: Oili ja Olli ovat syntyneet Tyynenmeren yllä mannertenvälisellä lennolla Aasiasta Amerikkaan. Kun Oili syntyi, oli 1. maaliskuuta. Kun Olli syntyi hieman myöhemmin, lentokone oli juuri ylittänyt kansainvälisen päivämäärärajan, jonka itäpuolella oli yhä 28. helmikuuta. Synttärijuhlista on tarkemmin muisteltuna aikaa jo reilut kolme vuotta, sillä kahden päivän ero saadaan tietenkin karkausvuosina.
 
Tämä pulma marssi vastaan Alex Bellosin pulmapalstalta The Guardianista.

4

Hoikka kolmio

|

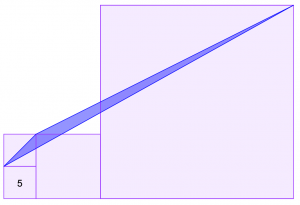
Pitkä pulmailutauko on hyvä katkaista Catriona Shearerin Twitterissä esittämällä kauniilla perusgeometrian ongelmalla. Oheisessa kuvassa on neljä neliötä. Vasemmassa alanurkassa olevan neliön pinta-ala on 5. Laske sinisen kolmion pinta-ala.

 

Ratkaisu:  Aloitetaan piirtämällä korkeusjana kolmiolle, jonka kanta on pienen neliön lävistäjä. Nyt huomataan, että koska isoimman neliön (jonka sivun pituutta ei tarvitse tietää!) lävistäjä on kolmion kannan suuntainen, voidaan kolmion huippupistettä siirtää mihin tahansa ison neliön lävistäjällä, eikä kolmion ala muutu. Korkeusjana säilyy ennallaan. Kun huippu saavuttaa ison neliön alakulman, voidaan kolmion ala laskea jo helposti kahden lävistäjän avulla, mutta ollaanpa hieman ahneempia!

Kun huippu on siirretty ison kolmion alakulmaan, voidaan kolmion vasemmanpuolimmainen kärkipiste siirtää vastaavalla tavalla pitkin pienen neliön lävistäjää kohti keskikokoisen neliön kulmaa. Koska myös tässä tarvittavat lävistäjät ovat yhdensuuntaiset, voidaan kolmio muokata alan muuttumatta suorakulmaiseksi kolmioksi, jonka pinta-ala on selvästi puolet keskimmäisestä neliöstä, eli kaksi kertaa pienen neliön ala. Kysytty ala on siis 10.

0

Mustat ässät

|

Päivölän opiston järjestämässä Pythagoraan polku -matematiikkakilpailussa oli tänä keväänä oivallinen tehtävä. Näin se kuuluu:

Ville ja Aapo pelaavat korttipeliä. Ville nostaa tavallisesta sekoitetusta 52 kortin pakasta kortteja yhden kerrallaan, kunnes saa mustan ässän. Tämän jälkeen Aapo jatkaa korttien nostamista niin kauan kunnes hänkin saa mustan mustan ässän. Voittaja on se, kumpi saa enemmän kortteja. Jos molemmat saavat yhtä monta korttia, peli päättyy tasan. Onko peli reilu? Mikäli ei, kummalla pelaajista on etu?

Kuva: Shrayas Rajagopal / Flickr (CC BY-NC-ND 2.0)

 

Ratkaisu: Ongelman voi ratkaista monin tavoin, mutta kaunein tuntemani ratkaisu ongelmaan kuuluu näin: ajatellaan, että mustat ässät jakavat pakan kolmeen osaan. Ensimmäisessä osassa ovat kortit, jotka ovat ennen ensimmäistä mustaa ässää, toinen osa on niiden välissä ja kolmas jälkimmäisen mustan ässän jälkeen. Nyt jäljelle jäävillä 50 kortilla on jokaisella yhtä suuri todennäköisyys päätyä mihin tahansa kolmesta osasta. Peli on siis reilu.

0

Ei ihan suorakulmainen kolmio

|

Suhteellisen pitkän tauon jälkeen on uuden pulman aika. Tämä pulma tuli (vähän eri muodossa) vastaan Presh Talwalkarin Mind Your Decisions -kanavalla YouTubessa.

Suorakulmaisen kolmion hypotenuusa on 10 ja hypotenuusalle piirretty korkeusjana on 6. Miksei kolmion ala ole 30?

Ratkaisu: Suorakulmaisia kolmioita, joiden hypotenuusa on 10, on useita. Koska samaa kaarta vastaava kehäkulma on puolet keskuskulmasta, voidaan kaikki tällaiset kolmiot muodostaa siten, että suoran kulman kärki valitaan puoliympyrältä, jonka halkaisija on 10. Tällöin puoliympyrän säde on 5, mikä on myös suurin mahdollinen korkeusjanan pituus. Siis tehtävänannon mukaista kolmiota ei voi olla edes olemassa!

0

Liikenneympyrä

|

Eipä olekaan hetkeen tullut käännetyksi Alex Bellosin pulmia, joten eiköhän liene korkea aika ottaa hänen tehtävälaaristaan yksi näppärä looginen ongelma. Bellos on saanut seuraavan pulman Pippa Suttonilta.

Adrian, Bruce, Clive, Dave ja Eddie ajavat ympyrää polkuautoilla, joiden rekisterinumerot ovat 1, 2, 3, 4 ja 5 (muttei välttämättä tässä järjestyksessä). He näkevät välittömästi edellään ja välittömästi takanaan ajavien rekisterinumerot, mutteivät omaansa. Lisäksi he kaikki ovat täydellisiä loogikkoja. He kuulevat kysymyksen:

”Ajatko autolla, jonka rekisterinumero on jonkin kokonaisluvun neliö?”

”En tiedä!” kuuluu vastaus kuin yhdestä suusta.

”Ajatko autolla, jonka rekisterinumero on jonkin kokonaisluvun neliö?” kuuluu kysymys uudestaan.

”En tiedä!” kaikki vastaavat, paitsi Eddie, joka vastaa ”En aja”.

Seuraavaksi ääni kysyy: ”Onko rekisterinumerosi suurempi kuin takanasi ajavalla?”

Dave huutaa, ettei tiedä. Tämän jälkeen Bruce ja Eddie sanovat, että ei ole, ja Adrian ja Clive toteavat, että on.

Mitkä ovat Adrianin, Brucen, Cliven, Daven ja Eddien rekisterinumerot?

Kuva: Tom/Flickr (CC BY 2.0)

Ratkaisu: Neliöitä rekisterinumeroista ovat 1 ja 4. Kukaan ei tietenkään voi tietää, ajaako itse neliönumeroisella autolla, mutta jos joku näkisi sekä edessään että takanaan neliön, voisi hän päätellä, että hän ei aja neliönumeroisella autolla. Ensimmäisellä kysymyksellä selviää, että kukaan ei näe kahta neliötä. Toisella kysymyksellä Eddie on onnistunut päättelemään, että koska kukaan ei näe kahta neliötä, eikä hän näe yhtään, että hänen autonsa ei ole neliönumeroinen. Eddien ilmoituksesta tiedetään myös heti, että autot 1 ja 4 kuuluvat Brucelle ja Clivelle, mutta järjestys ei vielä ole selvä.

Koska Dave ei tiedä, ajaako hänen takanaan häntä suurempi vai pienempi rekisteri, ei Cliven rekisteri voi olla 1. Siis Cliven rekisteri on 4 ja Brucen rekisteri on 1. Koska Eddie tietää, että hänen rekisterinsä on suurempi kuin Daven, ja koska Adrianin rekisteri on suurempi kuin Eddien, on Daven rekisteri 2, Eddien 3 ja Adrianin 5.

0

Neljäksi jaettu neliö

|

Paul Sloanen ja Des MacHalen kirjassa Mathematical Lateral Thinking Puzzles on yksinkertaisen näköinen ongelma, jonka ratkaiseminen ei olekaan ihan niin simppeliä.

Jaa neliö neljäksi suorakulmioksi siten, että nämä suorakulmiot voidaan järjestellä uudelleen kahdeksi erikokoiseksi neliöksi.

Ratkaisu: Oheisessa kuvassa on neliö, jonka sivun pituus on 5. Tällä tavalla leikaten se voidaan järjestellä neliöiksi, joiden sivujen pituudet ovat 3 ja 4. Sloanen ja MacHalen mukaan muita toimivia sivunpituussuhdekombinaatioita ei ole olemassa. Yllättävää!

0

Rekursiivinen rekursio

|

Kollegani Petri Kuukkanen antoi minulle melkoisen pirulaisen ratkottavaksi. Näin se kuuluu:

Järjestä luvut 1, 2, 3, \ldots, 9 lukujonoksi a_1, a_2, a_3, \ldots, a_9 niin, että

  • a_2=2 ja
  • a_n=a_{a_{n-1}}-1, kun n=2, 3, \ldots, 9.

Kuva: Bird Eye/Flickr (CC BY 2.0)

Ratkaisu: Pulma on varsin originaali, en ole törmännyt aiemmin tällaiseen, eikä ole Petrikään, joka pulman on laatinut. Hän on myös tarkastanut, ettei pulmaan löydy kuin yksi ratkaisu. Tietenkinhän pulma voidaan ratkoa myös kokeilemalla, mahdollisia järjestyksiä on vain 8!=40320 kappaletta, mutta mekaaninen ratkaisu olisi vähän tylsä. Mennään siis loogisella päättelyllä tekemääni ratkaisuun.

Poimitaan helpot ensin. Jo tehtävänanto lupaa, että a_2=2. Tästä seuraa heti, että a_3=a_{a_2}-1=a_2-1=2-1=1.

Seuraavaksi joudutaan jo vähän pohtimaan. Koska rekursiokaavan mukaan a_n=a_{a_{n-1}}-1, kun n=2, 3, \ldots, 9, on a_n<a_{a_{n-1}}. Koska a_1 kuuluu rekursiokaavan ulkopuolelle, on tehtävä johtopäätös, että koko jonon suurin termi on a_1=9. Tämän perusteella puolestaan ratkeaa, että a_4=a_{a_3}-1=a_1-1=9-1=8. Edelleen, koska a_2=a_{a_1}-1=a_9-1, saadaan termiksi a_9=a_2+1=2+1=3.

Järjestämättä ovat vielä arvot 4, 5, 6 ja 7 termeiksi a_5, a_6, a_7 ja a_8. Koska a_5=a_{a_4}}-1=a_8-1 ja koska a_8=a_{a_7}-1, niin a_5=a_{a_7}-2. Nyt minulle tuli hetkeksi tenkkapoo, ja myönnänkin edenneeni seuraavaan vaiheeseen arvaamalla1. Käytettävissä olevien lukujen nojalla tämä jättää vaihtoehdot a_5=4 tai a_5=5. Näistä vaihtoehto a_5=4 johtaa ristiriitaan (kokeile vain!).

Kun a_5=5, on edellä olleen yhtälön nojalla a_8=6. Nyt myös a_6=a_{a_5}-1=a_5-1=5-1=4 ja vielä a_7=a_{a_6}-1=a_4-1=8-1=7.

Koko jono on siis

    \[a_1=9, a_2=2, a_3=1, a_4=8, a_5=5, a_6=4, a_7=7, a_8=6, a_9=3.\]

0

Pormestarinvaali

|

Tuomo ja Mikko ovat pormestarinvaalin toisella kierroksella. Mikko saa lopulta m ääntä ja Tuomo t ääntä. Oletetaan, että annetut äänet nostetaan vaaliuurnasta yksi kerrallaan ja pidetään jatkuvasti kirjaa laskennan edistymisestä. Millä todennäköisyydellä ensimmäisen nostetun äänen jälkeen äänet ovat jossain ääntenlaskennan vaiheessa tasan?

 

0

Numerot järjestykseen

|

Kahdeksannumeroisessa luvussa on kaksi ykköstä, kaksi kakkosta, kaksi kolmosta ja kaksi nelosta. Ykköset ovat yhden numeron päässä toisistaan, kakkoset kahden numeron, kolmoset kolmen numeron ja neloset neljän numeron päässä toisistaan. Mikä luku on kyseessä?

Ratkaisu: Luku on 41312432 tai tämän peilikuva 23421314. Tämän pulman lähde on Futility Closet.