IMLS Digital Collections & Content / Flickr (CC BY 2.0)
Kaksi jokilaivaa lähtee samaan aikaan joen vastakkaisilta rannoilta tasaisella nopeudella suoraviivaisesti kohti vastarantaa; toinen laivoista on nopeampi. Kun laivat kohtaavat, on lähempi ranta 720 metrin päässä. Molemmat laivat pysähtyvät rannalle kymmeneksi minuutiksi, ja kun ne kohtaavat seuraavan kerran, ovat ne 400 metrin päässä toisesta rannasta. Kuinka leveä joki on?
Martin Gardnerin ongelma, tietenkin. Ratkaisu löytyy tästä. Ensi viikolle keksin sitten jotain ihan muuta.
…
![\[\begin{array}{ccccccccc} 0&1&2&3&4&5&6&7&\ldots\\ \updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&\\ 0&2&4&6&8&10&12&14&\ldots \end{array}\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-1f03460f3520c9b3c77fbc8ab959fb81_l3.png "Rendered by QuickLaTeX.com")
![\[\begin{array}{c|cccccccc} &1&2&3&4&5&6&7&\ldots\\ \hline 1&\frac{1}{1}&\frac{1}{2}&\frac{1}{3}&\frac{1}{4}&\frac{1}{5}&\frac{1}{6}&\frac{1}{7}&\ldots\\ 2&\frac{2}{1}&\frac{2}{2}&\frac{2}{3}&\frac{2}{4}&\frac{2}{5}&\frac{2}{6}&\frac{2}{7}&\ldots\\ 3&\frac{3}{1}&\frac{3}{2}&\frac{3}{3}&\frac{3}{4}&\frac{3}{5}&\frac{3}{6}&\frac{3}{7}&\ldots\\ 4&\frac{4}{1}&\frac{4}{2}&\frac{4}{3}&\frac{4}{4}&\frac{4}{5}&\frac{4}{6}&\frac{4}{7}&\ldots\\ 5&\frac{5}{1}&\frac{5}{2}&\frac{5}{3}&\frac{5}{4}&\frac{5}{5}&\frac{5}{6}&\frac{5}{7}&\ldots\\ 6&\frac{6}{1}&\frac{6}{2}&\frac{6}{3}&\frac{6}{4}&\frac{6}{5}&\frac{6}{6}&\frac{6}{7}&\ldots\\ 7&\frac{7}{1}&\frac{7}{2}&\frac{7}{3}&\frac{7}{4}&\frac{7}{5}&\frac{7}{6}&\frac{7}{7}&\ldots\\ 8&\frac{8}{1}&\frac{8}{2}&\frac{8}{3}&\frac{8}{4}&\frac{8}{5}&\frac{8}{6}&\frac{8}{7}&\ldots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots\\ \end{array}\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-060a79d684e00cd5f286e13863768b8b_l3.png "Rendered by QuickLaTeX.com")
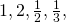(hypätään yli 
), 
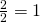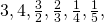(hypätään yli 
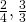ja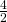 
), 
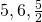ja niin edelleen.
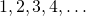välillä ilmeinen 1–1-vastaavuus. Pienellä vaivalla myös nolla sekä negatiiviset rationaaliluvut saadaan otettua mukaan luetteloon. Siis rationaalilukuja on ”yhtä monta” kuin luonnollisia lukuja.
pituuden tarkka arvo.
on ympyrän säde. Vastaus on siis tietenkin 10.![\[\frac{\frac{1}{50}}{1-\frac{1}{50}}=\frac{\frac{1}{50}}{\frac{49}{50}}=\frac{1}{49}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-85ac60ca0f81177206148d8b3f6654f3_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{1}{49}=\frac{1}{50}+\left(\frac{1}{50}\right)^2+\left(\frac{1}{50}\right)^3+\left(\frac{1}{50}\right)^4+\ldots .\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-86121ddf48677a00514675046b2d6e92_l3.png "Rendered by QuickLaTeX.com")
. Kerrotaan ensin osoittaja kahdella: 
. Luvun alku on siis 0,36. Edelleen 
, mutta koska 
, lisätään 1. Alku on siis 0,3673. Nyt 
, joten tästä jätetään ykkönen alusta pois. Olemme saaneet 0,367346. Ja kun tästä jatkamme, saamme ![\[\frac{18}{49}=0,367346938775510204081632\ldots.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-3833b0e1d3e5ffe2fae49091d7bde8e5_l3.png "Rendered by QuickLaTeX.com")
, 
ja 
.
, 
, 
, 
, 
ja 
. Huomaatko? Käytä apuna taitoasi 49:llä jakamisessa.
-koodauksen kanssa, enkä oikein meinaa löytää hyvää ratkaisua tähän. Tästä syystä lähiaikoina sivuilla nähtäneen monenlaisia kokeiluja sekä huonommin ja paremmin luettavaa matematiikkaa. Joka tapauksessa on selvää, että sivuston ulkoasu muuttuu sangen erilaiseksi, sillä nykyinen sivuteema ei taida tarpeisiini sittenkään kunnolla taipua. Kärsivällisyyttä, ystävät, kyllä tämä tästä ehkä.