Kahdestatoista samannäköisestä rahasta yksi on väärennetty. Se on joko hieman liian kevyt tai liian painava. Käytettävissä on tasapainovaaka. Mikä on vähin määrä punnituksia, jolla voit varmasti selvittää, mikä rahoista on väärä ja onko se liian kevyt vai liian painava?
Tarvittavien punnitusten määrä on kolme. Aloitetaan punnitsemalla molemmissa vaakakupeissa neljä kolikkoa. Jos punnitus on tasapainossa, on virheellinen kolikko neljän jäljelle jääneen joukossa. Näistä punnitaan kolme toisessa kupissa ja kolme oikeaa kolikkoa toisessa. Jos tämäkin on tasapainossa, on virheellinen kolikko löytynyt, ja kolmas punnitus osoittaa, onko se liian kevyt vai liian painava.
Jos taas kolme ”väärää” ja kolme oikeaa tuottaa epätasapainon, on löydetty se, onko haettu kolikko liian painava vai liian kevyt. Tämän jälkeen virheellinen yksilö löytyy laittamalla kolmesta mahdollisesta väärästä yksi kumpaankin vaakakuppiin. Tasapaino kertoo, että se kolmas on väärä, epätasapaino puolestaan sen, kumpi punnituista on väärän painoinen.
Tilanne muuttuu hankalammaksi, kun ensimmäinen 4+4-punnitus osoittaa epätasapainoa. Tämän jälkeen meillä on neljä ”painavaa”, neljä ”kevyttä” ja neljä varmasti oikeaa kolikkoa. Jatketaan nyt laittamalla kolme painavaa ja yksi kevyt toiseen kuppiin sekä yksi painava ja kolme oikeaa toiseen kuppiin. Mahdollisia tapauksia on nyt kolme.
Ensinnä, jos punnitus antaa tasapainon, on etsitty kolikko kolmen punnitsemattoman kevyen joukossa, joista se saadaan esille punnitsemalla yksi kolikko molemmissa kupeissa. Samaan tapaan virheellinen kolikko löytyy, mikäli punnitus osoittaa kolmen painavan kolikon puolen olevan edelleen painavampi.
Kolmas tapaus puolestaan on se, jos kolmen painavan kolikon puoli onkin nyt kevyempi. Tällöin joko yksinäinen painava kolikko on painavampi tai yksinäinen kevyt on kevyempi. Laittamalla kolmannessa punnituksessa nämä kaksi toiseen kuppiin ja kaksi oikeaa toiseen kuppiin ratkeaa epätasapainon suunnasta, kummasta kolikosta oli kyse.
Näin. Pirullinen ongelma sinänsä sangen yksinkertaisen tuntuisesta lähtötilanteesta.


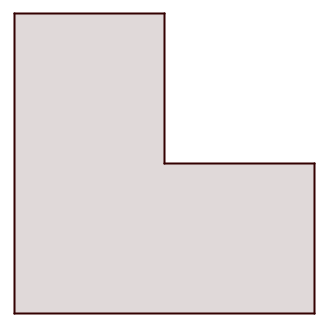

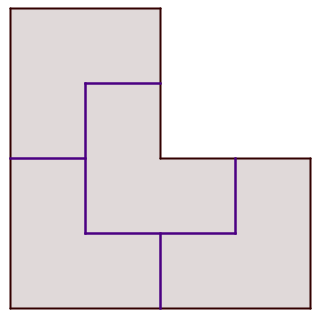

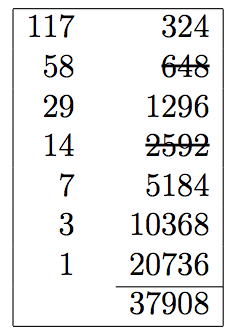
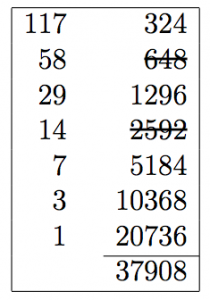 Otetaan esimerkiksi vaikkapa tulo
Otetaan esimerkiksi vaikkapa tulo