Pitkä pulmailutauko on hyvä katkaista Catriona Shearerin Twitterissä esittämällä kauniilla perusgeometrian ongelmalla. Oheisessa kuvassa on neljä neliötä. Vasemmassa alanurkassa olevan neliön pinta-ala on 5. Laske sinisen kolmion pinta-ala.
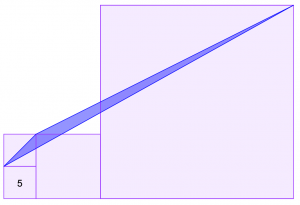
Ratkaisu: Aloitetaan piirtämällä korkeusjana kolmiolle, jonka kanta on pienen neliön lävistäjä. Nyt huomataan, että koska isoimman neliön (jonka sivun pituutta ei tarvitse tietää!) lävistäjä on kolmion kannan suuntainen, voidaan kolmion huippupistettä siirtää mihin tahansa ison neliön lävistäjällä, eikä kolmion ala muutu. Korkeusjana säilyy ennallaan. Kun huippu saavuttaa ison neliön alakulman, voidaan kolmion ala laskea jo helposti kahden lävistäjän avulla, mutta ollaanpa hieman ahneempia!
Kun huippu on siirretty ison kolmion alakulmaan, voidaan kolmion vasemmanpuolimmainen kärkipiste siirtää vastaavalla tavalla pitkin pienen neliön lävistäjää kohti keskikokoisen neliön kulmaa. Koska myös tässä tarvittavat lävistäjät ovat yhdensuuntaiset, voidaan kolmio muokata alan muuttumatta suorakulmaiseksi kolmioksi, jonka pinta-ala on selvästi puolet keskimmäisestä neliöstä, eli kaksi kertaa pienen neliön ala. Kysytty ala on siis 10.

10
Oikein!
Keskimmäinen neliö on alaltaan 20, koska sen sivu on 2*neliöjuuri(5), mutta isoin neliöhän voi olla ihan millainen vaan. Siis haluaisin kunnon lähtötiedot, en halua arvailla ison neliön kokoa (”onkohan sivultaan 3-kertainen”).
Vai voisiko tämä olla niin ovela tehtävä, että tulos ei riipu isoimman neliön koosta. Neliön kasvaessa sinisen kolmion kanta pitenee, mutta korkeus pienenee – mutta jos näin, on miksi isoin neliö on piirretty siten, että se näyttää sivultaan 3-kertaiselta viereiseen nähden.
Siis, alan miettiä tehtävää, kun saan tietää kumpi on oikea lähtötieto:
a) isoimman neliön sivu on 3-kertainen viereisen neliön sivuun
b) iso neliö voi olla minkäkokoinen hyvänsä (ehkei kuitenkaan viereistä pienempi – tai miksipä ehkä ei)
Toisaalta, jos valitsen b:n ja lasken alan tilanteessa, jos ”isoin” neliö on samankokoinen viereisen kanssa saan sinisen alaksi: 5*neliöjuuri(5)*neliöjuuri(5)/2=12,5 – siispä, jos kerran jossain tapauksessa saadaan sinisen alaksi 10, ei b-tulkinta ole oikea.
Menköön sitten a-tulkinnalla, vaikka protestoin: saan laskettua kaikki sinisen kolmion sivut Pythagoraan lauseella, ne ovat (J tarkoittaa neliöjuurta):
J(10), J(530) ja 20, minkä jälkeen saan todellakin Heronin kaavalla pinta-alaksi 10.
Mutta nyt kun tiedän, mitä kysytään, voin alkaa miettiä sitä kauniimpaa ratkaisua, jollain varmaankin on olemassa.
Lähtökohta on se, että isoimman neliön sivun pituutta ei tarvitse tietää.