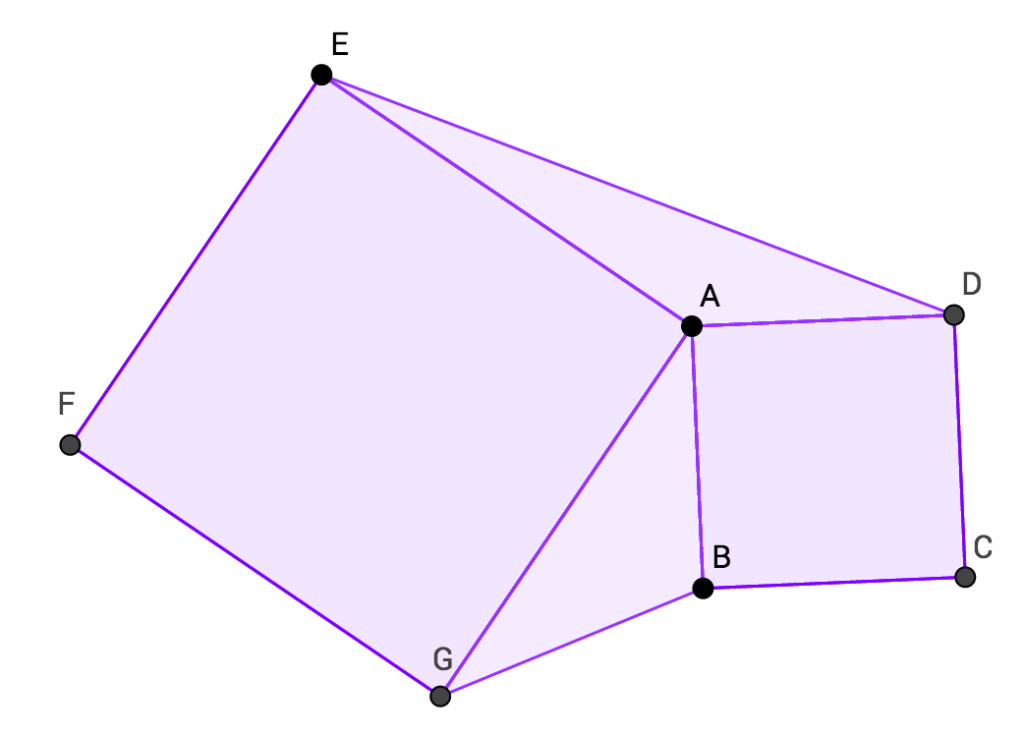
 Nyt on vuorossa perusgeometriaa! Oheisessa kuvassa
Nyt on vuorossa perusgeometriaa! Oheisessa kuvassa ![]() ja
ja ![]() ovat neliöitä. Osoita, että kolmioilla
ovat neliöitä. Osoita, että kolmioilla ![]() ja
ja ![]() on sama pinta-ala.
on sama pinta-ala.
Tämä pulma on Daniel Grillerin kirjasta Elastic Numbers. Löysin siihen helpon, mutta melko tylsän ratkaisun, joka on perusteltavissa lukiogeometrialla. Grillerin oma ratkaisu puolestaan on oleellisesti yksinkertaisempi ja kauniimpi. Sen ymmärtää alakoululainenkin! Siksipä tässä on sangen nätti viikon helppo pulma.
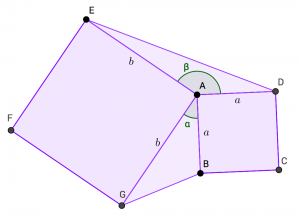
Kuva 1: Suplementtikulmat
Ratkaisu: Oma ideani perustui siihen, että koska kulmat ![]() ja
ja ![]() ovat suoria, ovat kulmat
ovat suoria, ovat kulmat ![]() ja
ja ![]() ovat suplementtikulmia, eli ne muodostavat yhdessä
ovat suplementtikulmia, eli ne muodostavat yhdessä ![]() kulman (kuva 1). Lukiotrigonometriassa opimme rakkaan työkalumme yksikköympyrän avulla, että kulmalla ja sen suplementtikulmalla on sama sini. Ja koska kolmion
kulman (kuva 1). Lukiotrigonometriassa opimme rakkaan työkalumme yksikköympyrän avulla, että kulmalla ja sen suplementtikulmalla on sama sini. Ja koska kolmion ![]() ala voidaan laskea kaavalla
ala voidaan laskea kaavalla ![]() , missä
, missä ![]() ja
ja ![]() ovat kulman
ovat kulman ![]() kyljet, ja yhtä lailla kolmion
kyljet, ja yhtä lailla kolmion ![]() ala on
ala on ![]() , niin selvästi kolmioiden alat ovat samat.
, niin selvästi kolmioiden alat ovat samat.
Joo, ei hirveän tyylikäs ratkaisu, mutta ratkaisu kuitenkin, ja itse tuloshan on varsin mukava.
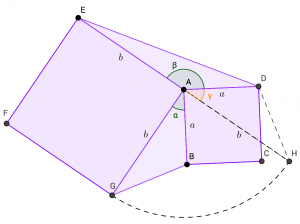
Kuva 2: Kierto pisteen A ympäri
Daniel Griller lähtee myös samasta ajatuksesta: ![]() . Mutta hän vie idean nokkelasti pidemmälle (Kuva 2). Koska
. Mutta hän vie idean nokkelasti pidemmälle (Kuva 2). Koska ![]() , voidaan kolmio
, voidaan kolmio ![]() kiertää 90 astetta pisteen
kiertää 90 astetta pisteen ![]() ympäri kolmioksi
ympäri kolmioksi ![]() , jossa
, jossa ![]() ja
ja ![]() (ja siis samalla
(ja siis samalla ![]() , joten pisteet
, joten pisteet ![]() ,
, ![]() ja
ja ![]() ovat samalla suoralla). Nyt meillä on kaksi kolmiota,
ovat samalla suoralla). Nyt meillä on kaksi kolmiota, ![]() ja
ja ![]() , joilla on sama kanta
, joilla on sama kanta ![]() ja sama korkeus, mistä ratkaisu välittömästi seuraa.
ja sama korkeus, mistä ratkaisu välittömästi seuraa.
