Seuraava pulma on Charles Lutwidge Dodgsonin alias Lewis Carrollin kirjasta Pillow-Problems vuodelta 1895. Kirjassa on 72 ongelmaa, jotka Dodgson kertoo kehitelleensä ja ratkoneensa päässänsä unettomina öinä. Kirjan ongelmien vaikeustaso vaihtelee hurjasta helpohkoihin, ehkäpä yläpäätä painottaen. Tämä ongelma on sieltä kevyemmästä päästä.
Viisi roistoa istuu ringissä ja jokaisella miehellä on yhtä monta penniä. Älykkäin heistä ehdottaa pientä pennipeliä. Ensinnäkin kaikki saavat numeron, älykkäin ykkösen, seuraava kakkosen, sitten kolmonen, nelonen ja vielä vitonen. Nyt älykkäin laittaa kaikki penninsä pussiin, antaa sen kolmoselle, jonka pitää ensin ottaa kummallekin naapurilleen pussista naapurin numeron osoittama määrä pennejä. Sitten kolmosen pitää laittaa pussiin puolet siitä määrästä pennejä, joka pussissa oli sen saapuessa hänelle. Sitten kolmonen antaa pussin vitoselle, joka antaa myös pussista pennit vierustovereille, lisää puolet siitä summasta, joka pussissa oli sen tullessa hänelle, ja antaa pussin kaksi paikkaa eteenpäin. Jos sattuisi käymään niin, että rahanlisäysvaiheessa itsellä ei olisi tarpeeksi rahaa pussin täydentämiseen, saisi kenen tahansa muun paitsi numero ykkösen pennipinosta täydentää puuttuvan määrän.
Kun pussi tulee takaisin ykköselle, hän nakkaa kaksi saamaansa rahaa pussiin, vetää pussin nyörit kiinni ja pakenee vauhdilla paikalta. Muut neljä roistoa jäävät hölmistyineinä katsomaan tyhjin käsin – ryökäle nappasi kaikki rahat! Kuinka monta penniä kullakin roistolla oli aluksi?
Ratkaisu: Olkoon kullakin konnalla aluksi ![]() kolikkoa. Peli etenee seuraavasti:
kolikkoa. Peli etenee seuraavasti:
- Numero
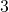 sai pussin jossa on
sai pussin jossa on 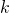 kolikkoa ja hän antoi pois
kolikkoa ja hän antoi pois 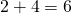 kolikkoa. Sitten hän laittaa pussiin
kolikkoa. Sitten hän laittaa pussiin 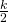 kolikkoa, joten pussiin jää
kolikkoa, joten pussiin jää 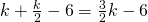 kolikkoa.
kolikkoa. - Numero
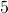 jakaa pois
jakaa pois 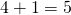 kolikkoa ja puolitoistakertaistaa pussissa olleen rahasumman. Loppusumma hänen vuoronsa jälkeen on siis
kolikkoa ja puolitoistakertaistaa pussissa olleen rahasumman. Loppusumma hänen vuoronsa jälkeen on siis 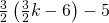 .
. - Numero
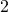 jakaa pois
jakaa pois 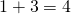 kolikkoa ja puolitoistakertaistaa pussin summan. Pussin rahamäärä on hänen jälkeensä
kolikkoa ja puolitoistakertaistaa pussin summan. Pussin rahamäärä on hänen jälkeensä 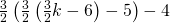 .
. - Numero
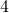 jakaa pois
jakaa pois 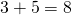 kolikkoa ja puolitoistakertaistaa pussin summan. Pussin rahamäärä on hänen jälkeensä
kolikkoa ja puolitoistakertaistaa pussin summan. Pussin rahamäärä on hänen jälkeensä 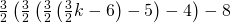 .
. - Numero
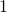 lisää pussiin kaksi kolikkoa, jonka jälkeen pussissa on
lisää pussiin kaksi kolikkoa, jonka jälkeen pussissa on 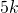 kolikkoa.
kolikkoa.
Tästä saadaan yhtälö
![]()
jonka ratkaisu on ![]() .
.
Sivumennen sanoen: olisi ehkä jäänyt ratkaisematta ilman kynän ja paperin apua. Eli onnea vain Lewis Carrollille, jos päässään yöllä tämän pyöritteli loppuun asti.
