Monthly Archives: maaliskuu 2016

0

Piste kolmiossa

|

Millä todennäköisyydellä umpimähkään valittu tasasivuisen kolmion sisällä oleva piste on lähempänä kolmion painopistettä kuin mitään kolmion sivuista?

Tämän pulman esitti Colin Beveridge Twitterissä. Pulma on hieman hankalampi kuin miltä se päälle päin näyttää, mutta se on ratkaistavissa ihan lukiotiedoilla.

Ratkaisu: 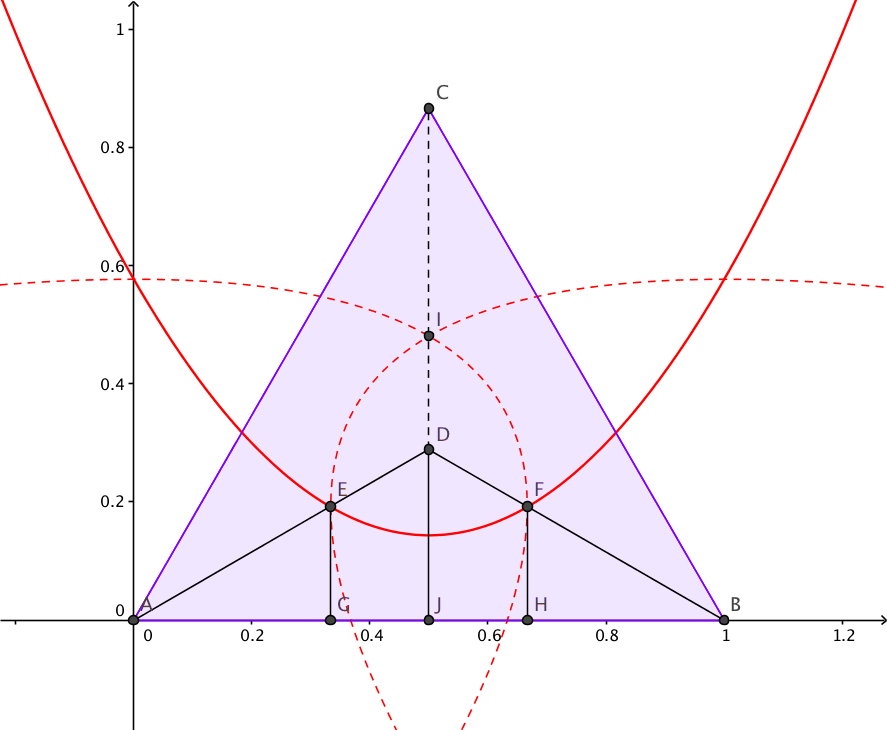pisteenetaisyysYleisyydestä luopumatta voimme sijoittaa kolmion yhden kärjen origoon ja asettaa sivun pituudeksi 1 yksikön. Tällöin painopisteen D koordinaatit ovat \left(\frac{1}{2},\frac{\sqrt{3}}{6}\right). Paraabeli on määritelmänsä mukaan niiden pisteiden joukko, jotka ovat yhtä etäällä annetusta pisteestä ja annetusta suorasta. Näin ollen kysyttyä aluetta rajaa kolme paraabelin kaarta, eli se jää pisteiden E, F ja I väliin. Symmetrian nojalla voidaan rajoittua kolmioon ABD. Tämän jälkeen tehtävä ratkeaa geometristä todennäköisyyttä soveltamalla.

Kolmion ABD ala on \frac{\sqrt{3}}{12}. Kolmioiden AGE ja BHF alat saadaan yhdenmuotoisuutta soveltamalla: Olkoon EG pystysuora. Nyt tasasivuisen kolmion puolikkaana kulmana kulma EAG=30^{\circ}, jolloin kulma GEA=60^{\circ}. Tästä seuraa, että \frac{EG}{EA}=\frac{1}{2}. Koska paraabelin määritelmän nojalla EG=ED, niin AE=\frac{2}{3}AD, jolloin kolmioiden AGE ja AJD yhdenmuotoisuuden vuoksi saadaan kolmion AGE alaksi (\frac{2}{3})^2\cdot \frac{1}{2}\cdot\frac{\sqrt{3}}{12}=\frac{\sqrt{3}}{54}. Symmetrian nojalla tämä on myös kolmion BHF ala.

Pisteiden E ja F kautta kulkevan paraabelin yhtälön selvittämiseksi huomataan ensin, että paraabelin huipun koordinaattien on oltava \left(\frac{1}{2},\frac{\sqrt{3}}{12}\right). Tästä saadaan paraabelille ns. huippumuotoinen yhtälö

    \[y-\frac{\sqrt{3}}{12}=a\left(x-\frac{1}{2}\right)^2,\]

Nyt, edellisen mittakaavatarkastelun perusteella saadaan paraabelin pisteelle E koordinaatit E=\left(\frac{1}{3},\frac{\sqrt{3}}{9}\right). Yllä olevan yhtälöön sijoittamalla saadaan, että a=\sqrt{3}. Pisteiden E, F, G ja H välinen ala saadaan määrättynä integraalina

    \[A_{EFGH}=\int_{\frac{1}{3}}^{\frac{2}{3}} \left(\sqrt{3}\left(x-\frac{1}{2}\right)^2+\frac{\sqrt{3}}{12}\right)dx=\frac{5}{54\sqrt{3}}.\]

Nyt siis kysytty todennäköisyys on

    \[\frac{A_{ABD}-A_{AGE}-A_{EFGH}-A_{BHF}}{A_{ABD}}=\frac{\frac{\sqrt{3}}{12}-\frac{\sqrt{3}}{54}-\frac{5}{54\sqrt{3}}-\frac{\sqrt{3}}{54}}{\frac{\sqrt{3}}{12}}=\frac{5}{27}.\]

Muokattu 31.3.2016: Lukijamme Kössi huomasi, että painopisteen y-koordinaatti oli kaksinkertainen oikeaan painopisteeseen verrattuna. Se on nyt korjattu oikeaksi, eli kolmion painopiste todella on \left(\frac{1}{2},\frac{\sqrt{3}}{6}\right). Lisäksi Kössi toivoi selvennystä siihen, miksi pisteet G ja H jakavat kannan AB suhteessa 1:1:1. Toivoakseni tämä muokattu ratkaisu vastaa nyt tuohonkin kysymykseen paremmin. Tarkempaa tehtävän analysointia ja vaihtoehtoisia ratkaisutapoja löytyy osoitteesta http://math.stackexchange.com/questions/1688936/what-is-the-probability-that-a-point-chosen-randomly-from-inside-an-equilateral.

0

Vedamatematiikkaa

|

Swāmī Bhāratī Kṛṣṇa Tīrtha (1884–1960) oli intialainen uskonoppinut ja matemaatikko, joka väitti kaiken matematiikan löytyvän muinaisista hindulaisista Veda-kirjoituksista johdetuista 16 suurasta ja 13 apusuurasta. Uskoo ken tahtoo (siis sen, mitä Swāmī Bhāratī Kṛṣṇa Tīrtha 1950-luvun lopulla kirjoittamassaan teoksessa väitti), mutta joka tapauksessa nämä yksinkertaiset säkeet antavat muutamia erittäin käyttökelpoisia – ja nopeita! – kikkoja päässälaskuun.

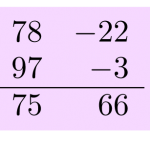Keskitytään nyt toiseen suuraan, jonka nimi on Nikhilam Navatashcaramam Dashatah1. Se tarkoittaa suunnilleen, että ”kaikki yhdeksästä ja viimeinen kymmenestä”. Siinä kerrotaan kaksi lukuavedamatikka keskenään käyttäen apuna niiden etäisyyttä lähimmästä kymmenen potenssista. Kaksinumeroisilla luvuilla laskettaessa käytetään referenssilukuna sataa, kolminumeroisilla tuhatta ja niin edelleen. Otetaan esimerkiksi tulo 78\cdot 97. Kirjoitetaan luvut allekkain ja laitetaan niiden viereen toiseen sarakkeeseen niiden etäisyydet luvusta 100. Nyt tulon kaksi viimeistä numeroa saadaan kertomalla oikeanpuoleisen sarakkeen luvut keskenään: -22\cdot (-3)=66. Jos tässä tulossa olisi enemmän kuin kaksi numeroa, menisivät sadat muistinumeroiksi alkuosuuteen, eli esimerkiksi jos oltaisiin saatu 840, olisivat viimeiset kaksi numeroa 40 ja 8 lisättäisiin tulon alkuosuuteen. Vastaavasti jos tässä tulossa olisi vähemmän kuin kaksi numeroa, lisättäisiin nollia eteen.

Toisessa vaiheessa voidaan edetä neljällä eri tavalla, jotka kaikki tuottavat saman tuloksen. Voidaan laskea saman diagonaalin luvut yhteen. Tai voidaan laskea yhteen vasemmanpuoleisen sarakkeen luvut ja vähentää 100. Tai edelleen voidaan laskea oikeanpuoleisen sarakkeen luvut yhteen ja lisätä 100. Kuinka tahansa toimitaankaan, tulos on aina sama: 78-3=97-22=78+97-100=-22-3+100=75. Tulon kaksi ensimmäistä numeroa ovat siis 75. Ja kaikkiaan 78\cdot 97=7566, kuten kuka tahansa voi tarkistaa.

Viikon helppona tehtävänä on osoittaa, miksi tämä menetelmä toimii aina kaksinumeroisille luvuille.

Entäpä jos tehtävänä olisikin laskea vaikkapa 103\cdot 87? Tai 514\cdot 522? Viikon vaikea pulma on miettiä, miten tätä samaa tekniikkaa voisi soveltaa myös näihin tuloihin.

Tämä temppu parin sukulaisensa kanssa tuli vastaan Alex Bellosin (ainakin ensimmäisen puoliskonsa perusteella aivan loistavassa) kirjassa Alex’s Adventures in Numberland (Bloomsbury, 2010).