Kulmanpuolittajien välinen kulma

Kuinka suuressa kulmassa suorakulmaisen kolmion terävien kulmien puolittajat leikkaavat? Entä yleistyykö tämä tulos myös muihin kolmioihin?

Ratkaisu: 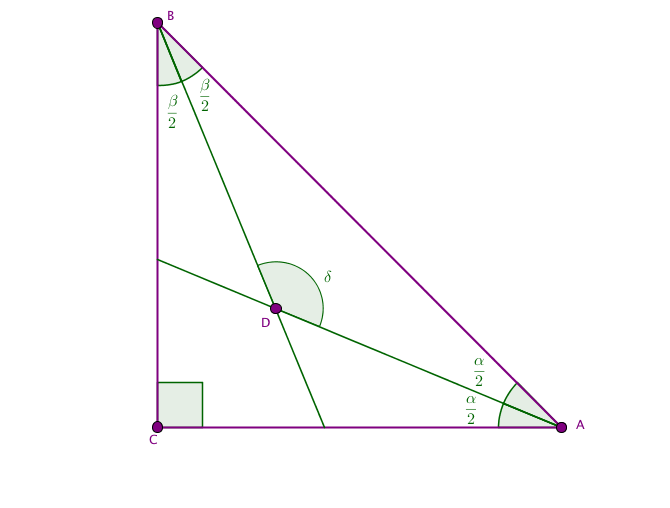kulmanpuolittajat

Tutkitaan kolmiota $ABC$ , jonka kulma $C$ on suora. Olkoot kulman $A$ suuruus $\alpha$ ja kulman $B$ vastaavasti $\beta$ . Näin ollen $\alpha + \beta = 90^{\circ}$ . Tutkitaan sitten kulmanpuolittajien ja hypotenuusan rajaamaa kolmiota $ABD$ . Nyt koska $\frac{\alpha}{2}+\frac{\beta}{2}+\delta=180^{\circ}$ , ja koska $\frac{\alpha}{2}+\frac{\beta}{2}=\frac{90^{\circ}}{2}=45^{\circ}$ , niin välttämättä $\delta=135^{\circ}$ . Toinen kulmanpuolittajien välisistä kulmista on tämän vieruskulma, eli $45^{\circ}$ .

Tulos on aika hauska ja toimii selvästi kaikissa suorakulmaisissa kolmioissa. Ihan yhtä nätisti tämä tulos ei kaikkiin kolmioihin yleisty, sillä jos alkuperäisen kolmion kolmas kulma olisi $\gamma$ , jäisi kulmanpuolittajien välisiksi kulmiksi tällöin $90^{\circ}+\frac{\gamma}{2}$ ja $90^{\circ}-\frac{\gamma}{2}$ .

Opettaja H:n pulmakulma

OpettajaH.fi

Vastaa Peruuta vastaus