 Pythagoras (n. 585–496 eaa.) oli antiikin Kreikan tunnetuimpia matemaatikkoja. Hän perusti esoteerisen koulukunnan, jossa matematiikkaan sotkettiin uskonnollisia elementtejä. Pythagoralaisesta koulukunnasta on peräisin paljon tiedettä – filosofiaa, matematiikkaa, uskontotiedettä ja musiikkia.
Pythagoras (n. 585–496 eaa.) oli antiikin Kreikan tunnetuimpia matemaatikkoja. Hän perusti esoteerisen koulukunnan, jossa matematiikkaan sotkettiin uskonnollisia elementtejä. Pythagoralaisesta koulukunnasta on peräisin paljon tiedettä – filosofiaa, matematiikkaa, uskontotiedettä ja musiikkia.
Ehkäpä tunnetuin matemaattinen tulos on Pythagoraan lause. Se ei ole Pythagoraan keksimä, sillä tulos tunnettiin jo satoja vuosia aiemmin monissa Välimeren alueen ja Lähi-Idän kulttuureissa. Pythagoraan lauseen mukaan suorakulmaisessa kolmiossa suoraa kulmaa vastaavan sivun (hypotenuusan) pituuden neliö on yhtä suuri suoran kulman kylkien (kateettien) neliöiden summan kanssa. Tai siis tutummin (ks. kuva): 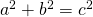 .
.
Pythagoraan lauseen toteuttavia lukukolmikoita kutsutaan Pythagoraan luvuiksi. Esimerkiksi 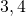 ja
ja 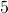 ovat Pythagoraan lukuja, sillä
ovat Pythagoraan lukuja, sillä 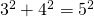 .
.
Pythagoraan luvuiksi kelpaavat melkein mitkä tahansa luvut, mutta eivät aivan mitkä tahansa. Osoita, että 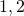 ja
ja 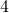 ovat ainoat luvut, jotka eivät voi olla lyhimpiä sivuja suorakulmaisessa kolmiossa, jonka kaikki sivut ovat kokonaislukuja.
ovat ainoat luvut, jotka eivät voi olla lyhimpiä sivuja suorakulmaisessa kolmiossa, jonka kaikki sivut ovat kokonaislukuja.
Ratkaisu: Tämä ongelma tuli mieleeni ihan äkkiseltään kesken matematiikan oppituntini, kun äkkäsin, kuinka mikä tahansa pariton luku ykköstä lukuunottamatta saadaan Pythagoraan kolmikon pienimmäksi luvuksi. Aloin tutkia aivan tietynlaisia lukukolmikkoja, joista pienin luku on pariton. 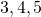 . Tai
. Tai 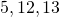 . Tai
. Tai 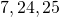 . Ja niin edelleen. Äkkiä tajusin, että tässä oleva kuvio yleistyy: mikä tahansa pariton luku voidaan laittaa pienimmäksi luvuksi sellaisessa Pythagoraan kolmikossa, jossa kaksi suurempaa lukua ovat peräkkäisiä. Tämä toimii, koska jokaisen parittoman luvun neliö on pariton, eli kahden peräkkäisen luvun summa. Ja juuri nämä ovat ne kaksi peräkkäistä lukua, jotka muodostavat pienimmän lukumme kanssa Pythagoraan kolmikon. Siis vaikkapa
. Ja niin edelleen. Äkkiä tajusin, että tässä oleva kuvio yleistyy: mikä tahansa pariton luku voidaan laittaa pienimmäksi luvuksi sellaisessa Pythagoraan kolmikossa, jossa kaksi suurempaa lukua ovat peräkkäisiä. Tämä toimii, koska jokaisen parittoman luvun neliö on pariton, eli kahden peräkkäisen luvun summa. Ja juuri nämä ovat ne kaksi peräkkäistä lukua, jotka muodostavat pienimmän lukumme kanssa Pythagoraan kolmikon. Siis vaikkapa 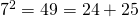 ja edelleen
ja edelleen 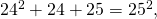 ja Pythagoraan lauseen mukainen tulos
ja Pythagoraan lauseen mukainen tulos 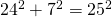 on valmis. Nyt voidaan heti sanoa, että koska
on valmis. Nyt voidaan heti sanoa, että koska 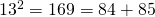 , niin varmasti
, niin varmasti 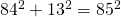 .
.
Tämän jälkeen tajusin nopeasti, että koska mikä tahansa Pythagoraan kolmikon monikerta on myös Pythagoraan kolmikko, ainoat mahdolliset luvut, jotka eivät voi olla Pythagoraan luvuista pienimpiä, ovat kakkosen potensseja. Nyt sain hieman apua kollegaltani Antti Saariselta, joka löysi kokeilemalla pari vastaesimerkkiä ensimmäiselle hypoteesilleni, että kakkosen potenssit jäävät kolmikoiden ulkopuolelle. Niinpä oli löydettävä vielä pienin kakkosen potenssi, joka sopii Pythagoraan kolmikkoon pienimmäksi.
Olkoon kolmiossa voimassa 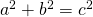 . Tällöin
. Tällöin 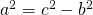 , joka puolestaan voidaan kirjoittaa muotoon
, joka puolestaan voidaan kirjoittaa muotoon 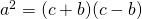 . On siis yritettävä löytää sellaiset luvut
. On siis yritettävä löytää sellaiset luvut 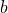 ja
ja  , että niiden summan ja erotuksen tulo olisi jokin kakkosen potenssi. Ja nyt
, että niiden summan ja erotuksen tulo olisi jokin kakkosen potenssi. Ja nyt 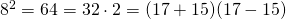 , mutta
, mutta 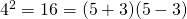 ei kelpaa. Myöskään luvuille
ei kelpaa. Myöskään luvuille 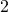 ja
ja 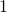 ei tällaista tuloa voida löytää.
ei tällaista tuloa voida löytää.
Näin ollen voidaan todeta, että 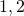 ja
ja 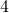 todellakin ovat ainoat positiiviset kokonaisluvut, jotka eivät voi olla lyhimpiä sivuja suorakulmaisessa kolmiossa, jonka kaikkien sivujen pituudet ovat kokonaislukuja. Se, onko tästä mitään hyötyä, on eri asia. Minun mielestäni tulos on kuitenkin sangen hauska.
todellakin ovat ainoat positiiviset kokonaisluvut, jotka eivät voi olla lyhimpiä sivuja suorakulmaisessa kolmiossa, jonka kaikkien sivujen pituudet ovat kokonaislukuja. Se, onko tästä mitään hyötyä, on eri asia. Minun mielestäni tulos on kuitenkin sangen hauska.
![]() . Sitten kysyt, mistä kaikista lapuista hänen lukunsa löytyy. Tämän jälkeen pamautat välittömästi hänen ajattelemansa luvun. Saat luvun helposti laskemalla yhteen ensimmäisen luvun jokaisesta lapusta, jonka toverisi mainitsee. Jos siis vaikka hän olisi ajatellut lukua
. Sitten kysyt, mistä kaikista lapuista hänen lukunsa löytyy. Tämän jälkeen pamautat välittömästi hänen ajattelemansa luvun. Saat luvun helposti laskemalla yhteen ensimmäisen luvun jokaisesta lapusta, jonka toverisi mainitsee. Jos siis vaikka hän olisi ajatellut lukua ![]() , hän olisi sanonut, että luku löytyy tauluista 1, 3 ja 4, jonka jälkeen laskisit vain
, hän olisi sanonut, että luku löytyy tauluista 1, 3 ja 4, jonka jälkeen laskisit vain ![]() .
.![]() nelibittiset binääriesitykset. Esimerkiksi
nelibittiset binääriesitykset. Esimerkiksi ![]() , eli se saadaan laskemalla
, eli se saadaan laskemalla ![]() . Jokainen luku, jossa viimeinen bitti on ykkönen, on lapussa 1. Vastaavasti toiseksi viimeistä ykköstä tarvitsevat luvut ovat lapussa 2, toisen bitin ykköset lapussa 3 ja ensimmäisen bitin ykköset lapussa 4.
. Jokainen luku, jossa viimeinen bitti on ykkönen, on lapussa 1. Vastaavasti toiseksi viimeistä ykköstä tarvitsevat luvut ovat lapussa 2, toisen bitin ykköset lapussa 3 ja ensimmäisen bitin ykköset lapussa 4.
 Pythagoras (n. 585–496 eaa.) oli antiikin Kreikan tunnetuimpia matemaatikkoja. Hän perusti esoteerisen koulukunnan, jossa matematiikkaan sotkettiin uskonnollisia elementtejä. Pythagoralaisesta koulukunnasta on peräisin paljon tiedettä – filosofiaa, matematiikkaa, uskontotiedettä ja musiikkia.
Pythagoras (n. 585–496 eaa.) oli antiikin Kreikan tunnetuimpia matemaatikkoja. Hän perusti esoteerisen koulukunnan, jossa matematiikkaan sotkettiin uskonnollisia elementtejä. Pythagoralaisesta koulukunnasta on peräisin paljon tiedettä – filosofiaa, matematiikkaa, uskontotiedettä ja musiikkia.

![Rendered by QuickLaTeX.com \[2016=\binom{2^{\binom{2^2}{2}}}{2}.\]](http://www.opettajah.fi/wp-content/ql-cache/quicklatex.com-e42b356b55fac6ad6d6138d0673f90f3_l3.png)