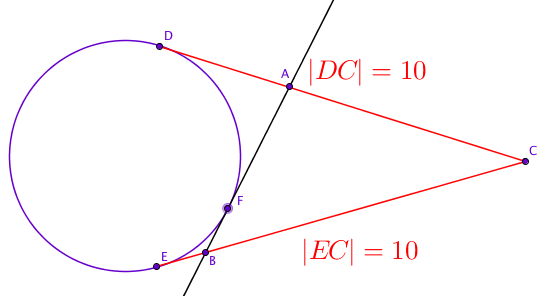
Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä . Tangenttien sivuamispisteet ja ovat etäisyydellä pisteestä . Piirretään ympyrälle vielä yksi tangentti pisteiden ja välisellä kaarella olevan pisteen kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet ja . Laske kolmion piiri.

Martin Gardner ainakin on tätä ongelmaa esitellyt.

Ratkaisu: Aivan vastaavasti kuin piste on tangenttikulman kärki, myös pisteet ja ovat. Voidaan helposti osoittaa, että tangenttikulman kärki on aina yhtä etäällä molemmista tangenttipisteistä, eli samaan tapaan kuin , voidaan myös todeta, että ja . Siis kolmion piiri on .