Buffonin neula

27.12.2015 | Opettaja H.

Gianluigi Buffon. Kuva: Nazionale Calcio/Flickr (CC BY 2.0)

Ei, jutun otsikko ei hauku Gigi Buffonia seulaksi. Otetaan sen sijaan käsittelyyn pulma, josta olin kuullut aiemminkin, muistaakseni noin vuonna 2009 Päivölän kansanopiston matematiikkalinjan Pythagoraan polku -kilpailun vierailuluennolla professori Robert Pichéltä. Mieleeni sen palautti Jordan Ellenbergin kirja How Not To Be Wrong. Ellenbergin kirja on myös tämän pulman ratkaisun lähteenä.

Nyt puhutaan nimittäin Georges-Louis LeClercistä, Buffonin kreivistä, joka vuonna 1733 toi ensi kerran geometrian ja todennäköisyyslaskennan yhteen. Lämmittelyksi voit tutustua vaikkapa tähän aiempaan ongelmaamme. Kolikonheitto-ongelman yleisen ratkaisun esitettyään kreivi Buffon lataa kovat piippuun.

Ajatellaan tasalevyisistä pitkistä lankuista koostuvaa lattiaa. Lattialle pudotetaan ohut neula, joka on täsmälleen lankkujen levyinen. Millä todennäköisyydellä neula putoaa lankun reunan päälle?

Kreivi Buffonin oma ratkaisu ongelmaan on tiukkaa matemaattista analyysiä, mutta pulma ratkeaa myös eräällä toisella tavalla, jossa tarvitaan vain hyvin yksinkertaisia matemaattisia apuvälineitä. Nimittäin yli sata vuotta Buffonin jälkeen Joseph-Émile Barbier esitti ratkaisun, joka perustuu odotusarvon käsitteeseen ja erityisesti sen additiivisuuteen, eli siihen, että useamman tapahtuman yhteinen odotusarvo on erillisten odotusarvojen summa. Otapa tästä vinkistä kiinni ja yritä ratkaista pulma!

Tämä on vuoden 2015 viimeinen Pulmakulman pulma, joten käytän samalla tilaisuuteni kiittää seurasta tämän blogin ensimmäisten kuukausien aikana. Minulla on ollut hauskaa, toivottavasti teilläkin!

Buffonin kreivin patsas Pariisin Jardin des Plantes’ssa. Kuva: Jean-Pierre Dalbéra/Flickr (CC BY 2.0)

Ratkaisu: On mahdollista, että neula joko putoaa reunan päälle tai sitten ei. Olkoon $p$ todennäköisyys sille, että neula putoaa reunalle. Tämän vastatapahtuma on se, että neula ei osu reunalle. Tämän todennäköisyys on $1-p$ . Näin pääsemme laskemaan odotusarvon reunan ja neulan leikkauspisteiden määrästä: $0\cdot (1-p)+1\cdot p=p$ ¹.

Koska odotusarvo on additiivin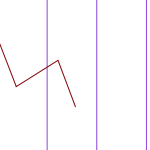en, eli $E(X+Y)=E(X)+E(Y)$ , voidaan päätellä, että kahden neulan pudottamisessa leikkauskohtien lukumäärän odotusarvo on $2p$ . Edelleen, jos pudotetaan vaikkapa kolme yhteenliitettyä neulaa, on odotusarvo leikkauspisteille $3p$ , sillä liittäminen ei vaikuta yksittäisen neulan osumatodennäköisyyteen.

Voidaan päätellä, että jos lankkujen väli on $a$ , niin miten tahansa väännellyn neulan, jonka pituus on $k\cdot a$ , leikkauskohtien odotusarvo on $k\cdot p$ . Eli esimerkiksi jos neulan pituus olisi $\pi\cdot a$ , olisi leikkauskohtien odotusarvo $\pi\cdot p$ . Ongelman loppuratkaisu onkin tässä.
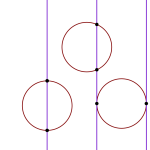Neula, jonka pituus on $\pi\cdot a$ , voidaan taivuttaa ympyräksi, jonka säde on $\frac{1}{2}a$ . Tällainen ympyrä osuu välttämättä lankkujen reunoille täsmälleen kahdesti. Siispä $\pi\cdot p =2,$ josta välittömästi

$p=\frac{2}{\pi}\approx 0,637.$

Tuomaan talo

21.12.2015 | Opettaja H.

Tuomas asuu kadulla, jonka talonnumerot ovat väliltä $8-100$ . Kössi tahtoo saada selville, mikä Tuomaan talon numero on.

Kössi kysyy, onko numero suurempi kuin $50$ . Tuomas vastaa, mutta valehtelee.

Seuraavaksi Kössi kysyy, onko numero jaollinen neljällä. Tuomas vastaa, mutta valehtelee taas.

Sitten Kössi kysyy, onko numero jonkin luvun neliö. Nyt, kaikkien hämmästykseksi, Tuomas vastaa totuudenmukaisesti.

Kössi sanoo, että jos Tuomas vielä kertoisi, onko ensimmäinen numero $3$ , hän tietäisi oikean talonnumeron. Tuomas vastaa Kössille, mutta emme tiedä, puhuiko hän totta. Tämän jälkeen Kössi ilmoittaa vastauksensa, joka valitettavasti on väärä.

Missä numerossa Tuomas oikeasti asuu?

Kuva: Bert Kaufmann/Flickr (CC BY-SA 2.0)

Ratkaisu: Kössi ei tietenkään tiedä, että Tuomas puhuu suurimman osan ajasta puhdasta palturia. Siksi Kössi perustaa veikkauksensa siihen, mitä Tuomas vastaa, ja se puolestaan vie meidät ratkaisun jäljille.

Koska ensimmäiseen kysymykseen Tuomas valehteli ja lopuksi Kössi haluaa tietää, onko ensimmäinen numero $3$ , on oikea talonnumero tietenkin suurempi kuin $50$ . Koska välillä $8-50$ on vain kaksi neljällä jaollista neliötä ( $16$ ja $36$ ) ja lukuisia sellaisia lukuja, jotka eivät ole joko jaollisia neljällä tai neliöitä tai kumpaakaan näistä, on Tuomas vastannut sekä neljälläjaollisuuskysymykseen (valheellisesti) että neliökysymykseen (todenmukaisesti) kyllä.

Tämä kaikki tarkoittaa sitä, että todellisuudessa Tuomas asuu talossa, jonka numero on suurempi kuin $50$ , ei ole neljällä jaollinen ja on jonkin luvun neliö. Ainoa kyseeseen tuleva talonnumero on $81$ .

Piraattien haaksirikko

16.12.2015 | Opettaja H.

Viimekertaisessa viikon vaikeassa viisi piraattia yritti päästä sopuun aarteen jakamisesta. Tämä aiheutti ymmärrettävästi pientä närää miesjoukon kesken. Niinpä tunteet olivatkin valmiiksi pinnassa, kun heitä kohtasi onnettomuus: heidän laivansa oli vuoro ajaa karille ja upota. Piraatit onnistuivat ajelehtimaan laudankappaleen varassa pienelle saarelle, jossa he lopen väsyneinä huomasivat, että saari oli täysin autio lukuunottamatta apinaa, joka leikki kookospähkinöillä. Kookospähkinöiden ohella muuta ravintoa ei ollut saatavilla. Piraatit sopivat, että kookospähkinät jaettaisiin aamulla tasan kaikkien kesken.

Ensimmäinen piraatti kuitenkin heräsi keskellä yötä. Hän ajatteli, että kukaan ei huomaisi, jos hän ottaisi oman osuutensa kookoksista jo nyt. Hän jakoi kookokset viiteen osaan, piilotti omansa ja palautti loput kasaan. Yksi kookospähkinä jäi ylitse, ja hän antoi sen apinalle. Sitten piraatti meni takaisin nukkumaan.

Toinen piraatti heräsi vähän myöhemmin. Hänkin jakoi kookokset viiteen osaan ja hautasi oman osuutensa syrjemmälle. Myös nyt jäi yksi kookospähkinä ylitse, ja hän antoi sen apinalle.

Kuva: Loke Seng Hon/Wikimedia Commons (CC BY-SA 3.0)

Ja kuten arvata saattaa, vuorollaan yön mittaan myös kolmas, neljäs ja viides piraatti kävivät erottelemassa oman osuutensa. Myös jokainen heistä antoi yhden ylimääräisen kookoksen apinalle.

Aamulla piraatit heräsivät ja huomasivat, että kookospähkinäkasa oli yön mittaan hieman vajunut. He eivät kuitenkaan sanoneet mitään, vaan jakoivat kookokset viiteen osaan. Apinakaan ei jäänyt ilman: yksi kookos jäi ylitse.

Kuinka monta kookospähkinää saarella vähintään oli?

Ratkaisu: Tämä ongelma voidaan ratkaista ainakin parilla eri tavalla. Puhdas kokeileminen eri kookospähkinämäärillä on tietenkin yksi mahdollisuus, mutta luulenpa, että kärsivällisyyden rajat tulevat vastaan…

Lähdetään mieluummin mallintamaan tilannetta. Olkoon kookospähkinöiden lukumäärä $n$ . Apina saa siis jokaisella jakokierroksella yhden pähkinän, jolloin eri jakokerroista saadaan seuraava taulukko.

$\begin{array}{|l|l|l|} \hline &\mbox{Piraatille}&\mbox{Kasaan}\\ \hline 1&\frac{1}{5}(n-1)&\frac{4}{5}(n-1)\\ 2&\frac{1}{5}(\frac{4}{5}(n-1)-1)&\frac{4}{5}(\frac{4}{5}(n-1)-1)\\ 3&\frac{1}{5}(\frac{4}{5}(\frac{4}{5}(n-1)-1)-1)&\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(n-1)-1)-1)\\ 4&\frac{1}{5}(\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(n-1)-1)-1)-1)&\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(n-1)-1)-1)-1)\\ 5&\frac{1}{5}(\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(n-1)-1)-1)-1)-1)&\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(\frac{4}{5}(n-1)-1)-1)-1)-1)\\ \hline \end{array}$

No niin. Aamulla tilanne on siis tämä, eikä yhdelläkään unenpöpperöisellä merirosmolla ole enää mukavaa näiden lausekkeiden kanssa. Tilanne ei ole ollenkaan niin paha kuin miltä se näyttää, sillä voidaan sanoa, että jollakin kokonaisluvulla $k$ pätee

$\frac{4}{5}\left(\frac{4}{5}\left(\frac{4}{5}\left(\frac{4}{5}\left(\frac{4}{5}\left(n-1\right)-1\right)-1\right)-1\right)-1\right)=5k+1,$

eli jos apina saa yhden kookoksen, on jaettava kookoskasa viidellä jaollinen. Nyt yhtälön vasemmalle puolelle muodostuu geometrinen summa, jonka suhdeluku on $\frac{4}{5}$ :

$\left(\frac{4}{5}\right)^5 n-\left(\frac{4}{5}\right)^5-\left(\frac{4}{5}\right)^4-\left(\frac{4}{5}\right)^3-\left(\frac{4}{5}\right)^2-\frac{4}{5}\right=5k+1,$

josta geometrisen summan laskukaavaa hyödyntäen saamme

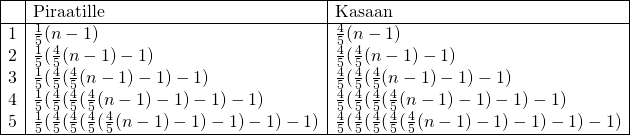
$\left(\frac{4}{5}\right)^5 n-\frac{4}{5}\cdot\frac{1-\left(\frac{4}{5}\right)^5 }{1-\frac{4}{5}}=5k+1.$

Kun tätä yhtälöä kerrotaan puolittain luvulla $5^5=3125$ ja siirrellään hieman termejä yhtäsuuruusmerkin ylitse, saamme seuraavan Diofantoksen yhtälön:

$1024n=15625k+11529.$

Diofantoksen yhtälöllä tarkoitetaan kokonaislukukertoimista vähintään kahden muuttujan yhtälöä, jolle etsitään kokonaislukuratkaisuja. Ne ovat saaneet nimensä noin 200-luvulla eläneen Diofantos aleksandrialaisen mukaan, joka oli aikansa merkittävimpiä matemaatikkoja. Yleistä ratkaisukaavaa näille yhtälöille ei ole olemassa, mutta joitakin erikoistapauksia voidaan ratkaista mekaanisin menetelmin. Onneksi meidän yhtälömme osuu yhteen näistä ”helpoista” tapauksista: nimittäin Diofantoksen yhtälöllä $xa+yb=c$ on aina ääretön määrä ratkaisuja, mikäli lukujen $a$ ja $b$ suurin yhteinen tekijä jakaa luvun $c$ .

Tehdään tekninen muuttujanvaihto $m=-k$ , jolloin yhtälömme voidaan kirjoittaa muotoon $1024n+15625m=11529.$ Koska $1024=2^{10}$ ja $15625=5^6$ , on varmasti näiden suurin yhteinen tekijä $1$ , joten ratkaisuja on olemassa. Riittää löytää pienin sellainen positiivinen arvo luvulle $n$ , että $m$ on negatiivinen.¹

Ensin tarvitaan yksi ratkaisu yhtälölle. Tämä voidaan tehdä joko Eukleideen algoritmin avulla tai sitten ihan vain löytämällä. Äskeisestä yhtälön sievennyksestä voidaan nähdä, että jos $n_0=-4$ ja $m_0=1$ , on yhtälö tosi. Tällöin yleinen ratkaisu saadaan kaavalla

$\begin{cases} n=-4+15625t\\ m=1-1024t \end{cases}, t\in\mathbb{Z}.$

Nyt sijoittamalla $t=1$ saadaan $n=15621$ , joka on pienin mahdollinen kookospähkinöiden määrä.

Tangenttikolmio

15.12.2015 | Opettaja H.

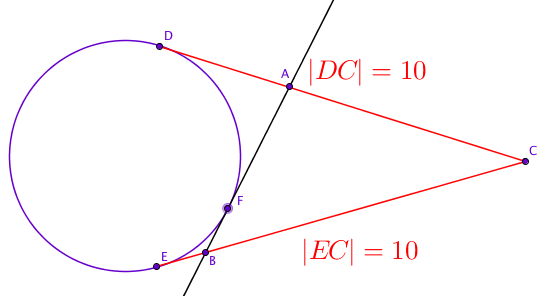Näyttökuva 2015-12-11 kello 15.46.15 Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä $C$ . Tangenttien sivuamispisteet $D$ ja $E$ ovat etäisyydellä $10$ pisteestä $C$ . Piirretään ympyrälle vielä yksi tangentti pisteiden $C$ ja $D$ välisellä kaarella olevan pisteen $F$ kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet $A$ ja $B$ . Laske kolmion $ABC$ piiri.

Martin Gardner ainakin on tätä ongelmaa esitellyt.

Ratkaisu: Aivan vastaavasti kuin piste $C$ on tangenttikulman kärki, myös pisteet $A$ ja $B$ ovat. Voidaan helposti osoittaa, että tangenttikulman kärki on aina yhtä etäällä molemmista tangenttipisteistä, eli samaan tapaan kuin $|DC|=|EC|$ , voidaan myös todeta, että $|AD|=|AF|$ ja $|BE|=|BF|$ . Siis kolmion $ABC$ piiri on $20$ .

Vaarin elukat

11.12.2015 | Opettaja H.

Koska viikon vaikea merirosvopulma ratkesikin perusteellisesti ja tyylikkäästi alta aikayksikön kommentaattorimme Tonin toimesta (mutta älä heti katso sinne kommenttiosion ratkaisuun – yritä itse!), laitetaan peliin vielä yksi ongelma, joka kuuluu kategoriaan viikon vitsi. Voi olla, että jatkossa nämä ajoittaiset huumoripalat joko yleistyvät tai sitten eivät. Joka tapauksessa Martin Gardnerin ehtymättömillä laareilla jälleen lusikoidaan.

Vaarin maatilalla oli 20 kanaa, 40 lehmää ja 60 hevosta. Montako hevosta vaarilla on, jos lehmät lasketaan hevosiksi?

Kuva: Eduardo Amorim/Flickr (CC BY-SA 2.0)

Ratkaisu: Hevosia on 60. Ei lehmästä tule hevosta, vaikka se hevoseksi laskettaisiinkin.

Lentävän hollantilaisen aarre

11.12.2015 | Opettaja H.

Johann Gehrts (1887): Lentävä hollantilainen/Wikimedia Commons (Public Domain)

Tämänkertainen viikon vaikea vie meidät merta edemmäs, tarkkaan ottaen Itämerta edemmäs, sillä pulma löytyi hollantilaiselta The Ultimate Puzzle Site -sivustolta.

Lentävä hollantilainen haaksirikkoutui, ja viiden merirosvon kopla on saanut haltuunsa 1000 kultarahan aarteen. Nämä eivät olekaan mitään aivan tavanomaisia piraatteja, vaan heillä kaikilla on kolme yhtenevää piirrettä:

He ovat ahneita. He haluavat niin paljon rahaa kuin vain ikinä saavat.
He ovat verenhimoisia. He vaikka tappavat toverinsa, jos hyötyvät siitä.
He ovat täydellisen loogisia optimoijia. He tekevät aina itselleen tuottoisimmat päätökset.

Nyt merirosvojen pitäisi siis jakaa 1000 rahan aarre. He menettelevät seuraavasti. Merirosvot on järjestetty tiukkaan arvojärjestykseen ensimmäisestä viidenteen ja jokaisella merirosvolla on vuorollaan yksi mahdollisuus ehdottaa omasta mielestään sopivaa rahanjakoa. Jos enemmistö merirosvoista hyväksyy jaon, rahat jaetaan esityksen mukaan. Jos taas ehdotus ei saa enemmistöä taakseen, heitetään ehdottaja armotta yli laidan haita kuhisevaan mereen.

Mitä ensimmäinen merirosvo ehdottaa?

Touko-tontun toivekierros

8.12.2015 | Opettaja H.

Touko-tonttu lähtee Korvatunturilta keräämään lapsukaisten joululahjatoiveita. Hän tarvitsee koko kierrokseensa kuusi päivää, jonka jälkeen hän on jälleen takaisin Korvatunturilla.

Valitettavasti Touko-tontun tarvitsee myös syödä matkalla. Koska silkohapsien kirjeet vievät paljon tilaa, ja koska tontun ruoka on melko painavaa, ei Touko voi kantaa mukanaan kuin neljän päivän ruokavarat. Tontunruokaa saa vain Korvatunturilta, joten Touko on vaarassa nääntyä nälkään!

Ellei sitten.

Toukohan voi ottaa mukaansa tonttukavereita Korvatunturilta! Jokainen tonttu pystyy kuitenkin kantamaan vain neljän päivän ruokavarat mukanaan ja jokainen syö päiväannoksen ruokaa joka päivä. Yhtäkään tonttua ei saa näännyttää nälkään eikä jättää matkan varrelle ja kukin tonttu saa lähteä Korvatunturilta vain kerran. Sosiaalisena eläimenä tonttu voi jakaa omista ruokavaroistaan (kokonaisia päiväannoksia) muille.

Kuinka monta tonttua Touko vähintään tarvitsee mukaansa Korvatunturilta?

Tämä ongelma osui silmiini Alex Bellosin pulmapalstalta The Guardianissa. Se on ilmeisesti saksalaista alkuperää.

Ratkaisu: On selvää, ettei Touko selviä yksin. Pienellä kokeilulla huomataan myös, että yksi kaveri ei riitä. Kaksi aputonttua sen sijaan on tarpeeksi.

Touko ja kaksi aputonttua starttaavat Korvatunturilta kontit täynnnä ruokaa. Ensimmäisen päivän jälkeen ensimmäinen aputonttu antaa yhden appeen Toukolle ja toisen toiselle tontulle. Nyt ensimmäiselle tontulle jää yksi ruoka kotimatkaa varten, Toukon ja toisen tontun ruokavarastot ovat jälleen täynnä. Toisen päivän jälkeen toinen tonttu antaa yhden päivän sapuskat Toukolle ja suuntaa kahden oman ruokapakettinsa kanssa kohti kotia. Toukolla on nyt ruokaa neljäksi päiväksi, joten loppumatkan hän selviää yksinään.

Ympyrä säännöllisen monikulmion ympärillä

1.12.2015 | Opettaja H.

Säännöllisellä monikulmiolla tarkoitetaan monikulmiota, jonka kaikki sivut ovat yhtä pitkät ja kaikki kulmat yhtä suuret. Niitä on tutkittu käytännössä niin kauan kuin matematiikkaa yleensäkin on tutkittu.

Yksi hyvin tunnettu säännöllisten monikulmoiden sovelluskohde on ympyrän piirin ja pinta-alan arviointi. Jo ammoin ymmärrettiin, että kaikkien ympyröiden piirin ja halkaisijan suhde oli sama: piiri on hieman yli kolminkertainen halkaisijaan nähden. Nykyään tätä suhdetta merkitään symbolilla $\pi$ . Luku $\pi$ on irrationaaliluku, eli päättymätön jaksoton desimaaliluku. Sitä on vuosituhansien saatossa arvioitu monin tavoin, josta tässä paneudumme nyt ympyrän sisään piirrettyihin säännöllisiin monikulmioihin.

Ympyrän sisään piirretyllä monikulmiolla tarkoitetaan monikulmiota, jonka kaikki kärjet ovat ympyrän kehällä. Säännöllisen monikulmion ympäri voidaan aina piirtää ympyrä, vaikka yleisesti kaikilla monikulmioilla tätä ominaisuutta ei ole. Säännöllisen monikulmion keskipiste ja sen ympäri piirretyn ympyrän keskipiste yhtyvät.

Jos säännöllisen monikulmion sivujen lukumäärää kasvatetaan, saadaan yhä parempia arviota ympyrän pinta-alalle ja sitä kautta myös luvulle $\pi$ . Voidaan (melko) helposti osoittaa, että kun monikulmion sivujen lukumäärä kasvaa rajatta, monikulmion alan raja-arvo on ympyrän ala $\pi r^2$ . Kuvia katsomalla tämä toki näyttää ilmeiseltä, mutta matematiikassa mikään ei ole varmaa ennen kuin se on oikeasti todistettu.

Viikon vaikea kysymys on seuraava. Kuinka monisivuinen ympyrän sisään piirretty säännöllinen monikulmio tarvitaan, jotta monikulmion ala olisi korkeintaan $0,1$ prosenttia pienempi kuin ympyrän ala?

PS. Arkhimedes pääsi jo 200-luvulla eaa. huiman hyvään arvioon $3\frac{10}{71}<\pi<3\frac{1}{7}$ . Hän käytti tiettävästi apunaan ympyrän ympäri ja sisään piirrettyä säännöllistä 96-kulmiota!

Ratkaisu: Säännöllinen $n$ -kulmio voidaan aina jakaa $n$ yhtenevään tasakylkiseen kolmioon, joiden kanta on monikulmion sivu ja kylkinä monikulmion keskipisteen ja kärjen yhdysjana. Tässä tapauksessa tämä yhdysjana on tietenkin ympyrän säde. Kolmioiden huippukulma on $\frac{360^{\circ}}{n}$ , joten kolmioiden yhteenlasketuksi pinta-alaksi saadaan

$A_{kolmiot}=n\cdot\frac{1}{2}r^2\cdot \sin \frac{360^{\circ}}{n}.$

Tehdään tässä vaiheessa muutama muutos käytettäviin lukuihin. Ensinnäkin, muutetaan kulman suuruus radiaaneiksi. $360^{\circ}=2\pi$ (rad), joten alan lausekkeeksi saadaan nyt $A_{kolmiot}=n\cdot\frac{1}{2}r^2\cdot \sin \frac{2\pi}{n}.$ Tehdään vielä toinen tekninen vaihdos vähäksi aikaa: olkoon $\frac{2\pi}{n}=x,$ joten $\frac{2\pi}{x}=n$ , josta edelleen

$A_{kolmiot}=\frac{2\pi}{x}\cdot\frac{1}{2}r^2\cdot \sin x=\pi r^2\cdot \frac{\sin x}{x}.$

Ympyrän ala on tietenkin $\pi r^2$ , joten kysytty suhde

$\frac{A_{kolmiot}}{A_{ympyrä}}=\frac{\pi r^2\cdot \frac{\sin x}{x}}{\pi r^2}=\frac{\sin x}{x}.$

Tutkitaan seuraavaksi lausekkeen $\frac{\sin x}{x}$ käyttäytymistä. Koska $\frac{2\pi}{n}=x,$ niin sivujen lukumäärän $n$ kasvaessa rajatta $x\to 0$ . On tilanneyhteydestä ilmeistä, että nyt $\frac{\sin x}{x}\to 1$ , kun $x\to 0$ mutta kuinka se todistetaan? Ja edelleen (ja tässä onkin varsinainen kysymyksemme): kuinka suuri luvun $n$ on oltava, tai siis kuinka pieni luvun $x$ on oltava, jotta $\frac{\sin x}{x}>0,999$ . Vastaus molempiin kysymyksiin voidaan etsiä monin tavoin. Niistä yksi hienoimmista on ns. Taylorin sarja.

Sinifunktio voidaan esittää päättymättömänä summana eli sarjana

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots,$

joten lauseke $\frac{\sin x}{x}$ voidaan sieventää muotoon

$\frac{\sin x}{x}=\frac{x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots$

Tämän lausekkeen arvo lähestyy selvästi arvoa $1$ , kun $x\to 0$ . Edelleen tätä lauseketta voidaan arvioida vain paria ensimmäistä termiä käyttäen. Siis lähellä nollaa

$\frac{\sin x}{x}\approx 1-\frac{x^2}{3!}.$

Näin ollen oikea suuruusluokka ratkaisulle saadaan epäyhtälöstä $1-\frac{x^2}{3!}>0,999$ , josta $0<x<\sqrt{0,006}.$ (Ei-positiivinen osa epäyhtälön ratkaisusta voidaan nyt sivuuttaa.) Takaisin alkuperäiseen muuttujaan $n$ palaten saamme

$\frac{2\pi}{n}<\sqrt{0,006},$

josta edelleen $n>81,11\ldots$ . Koska tämä oli alkujaankin likiarvo, tarkistetaan vielä saadut arvot sijoittamalla lausekkeeseen $\frac{\sin x}{x}$ luvun $n$ arvoja $81$ ja $82$ vastaavat arvot $x=\frac{2\pi}{81}$ ja $x=\frac{2\pi}{82}$ :

$\frac{\sin \frac{2\pi}{81}}{\frac{2\pi}{81}}\approx 0,99897<0,999; \quad \quad \frac{\sin \frac{2\pi}{82}}{\frac{2\pi}{82}}\approx 0,99902>0,999.$

Näin ollen vastaus kysymykseen on siis vähintään säännöllinen $82$ -kulmio.

Ratkaisuun liittyvää Geogebra-applettia voi tutkia tämän linkin kautta.

Opettaja H:n pulmakulma

OpettajaH.fi

Monthly Archives: joulukuu 2015

Buffonin neula

Tuomaan talo

Piraattien haaksirikko

Tangenttikolmio

Vaarin elukat

Lentävän hollantilaisen aarre

Touko-tontun toivekierros

Ympyrä säännöllisen monikulmion ympärillä

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon:

Pistä kiertoon: