Ystäväni Tuomas Salo törmäsi Moskovan-vierailullaan viime vuosituhannen lopulla seuraavaan oivallisen kauniiseen pulmaan.
Valitaan mielivaltaisesti piste ![]() positiiviselta
positiiviselta ![]() -akselilta väliltä
-akselilta väliltä ![]() ja piste
ja piste ![]() positiiviselta
positiiviselta ![]() -akselilta väliltä
-akselilta väliltä ![]() . Valitaan piste
. Valitaan piste ![]() mistä tahansa origokeskisen yksikköympyrän kehältä koordinaatiston ensimmäisestä neljänneksestä. Osoita, että kolmion
mistä tahansa origokeskisen yksikköympyrän kehältä koordinaatiston ensimmäisestä neljänneksestä. Osoita, että kolmion ![]() piiri on enemmän kuin
piiri on enemmän kuin ![]() .
.
Ellet muuten usko, voit liikutella pisteitä oheisessa Geogebra-appletissa. Jos appletti ei näy tässä, voit leikkiä sillä Geogebratubessakin.
Ratkaisu: Tämän ongelman voinee ratkaista algebrallakin – Pythagoraan lausetta ja muutamia luotaantyöntäviä yhtälöitä ja niin edelleen. Seuraava ratkaisu on kuitenkin kauneudessaan ilmiömäinen ja, mikä tärkeintä, täysin riittävä.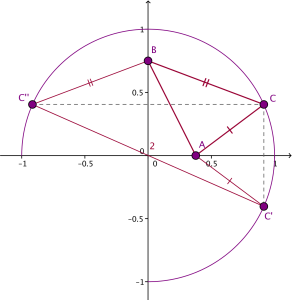
Peilataan piste ![]()
![]() – ja
– ja ![]() -akseleiden suhteen pisteiksi
-akseleiden suhteen pisteiksi ![]() ja
ja ![]() .Nyt symmetrian nojalla janat
.Nyt symmetrian nojalla janat ![]() ja
ja ![]() ovat keskenään yhtä pitkät, samoin janat
ovat keskenään yhtä pitkät, samoin janat ![]() ja
ja ![]() . Näin ollen kolmion
. Näin ollen kolmion ![]() piiri on sama kuin murtoviivan
piiri on sama kuin murtoviivan ![]() pituus. Koska
pituus. Koska ![]() on ympyrän halkaisija, ja siis pituudeltaan
on ympyrän halkaisija, ja siis pituudeltaan ![]() , on kysytty piiri selvästi tätä pidempi.
, on kysytty piiri selvästi tätä pidempi.
