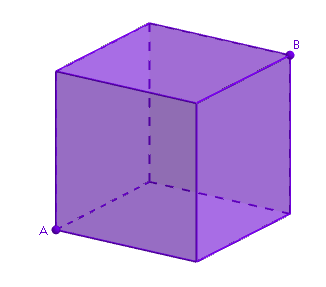
 Muurahainen lähtee liikkeelle kuution kärjestä
Muurahainen lähtee liikkeelle kuution kärjestä ![]() ja etenee kuution särmiä pitkin. Kun muurahainen tulee johonkin kärkeen, se valitsee sattumanvaraisesti seuraavan särmän, jota pitkin se lähtee kulkemaan (se voi siis myös palata takaisin kohti kärkeä, josta se juuri lähti). Millä todennäköisyydellä muurahainen päätyy kärkeen
ja etenee kuution särmiä pitkin. Kun muurahainen tulee johonkin kärkeen, se valitsee sattumanvaraisesti seuraavan särmän, jota pitkin se lähtee kulkemaan (se voi siis myös palata takaisin kohti kärkeä, josta se juuri lähti). Millä todennäköisyydellä muurahainen päätyy kärkeen ![]() täsmälleen kolme särmää kuljettuaan?
täsmälleen kolme särmää kuljettuaan?
Ratkaisu: Jokaisessa kärjessä muurahaisella on kolme vaihtoehtoa seuraavalle suunnalle, joten erilaisia kolmen särmän reittejä on tuloperiaatteen mukaan ![]() .
.
Mietitään sitten, kuinka moni reiteistä vie kolmea särmää pitkin kärkeen ![]() . Kärki
. Kärki ![]() on ainoa kärki, josta etäisyys kärkeen
on ainoa kärki, josta etäisyys kärkeen ![]() on
on ![]() särmää. Kustakin kärjestä, johon kärjestä
särmää. Kustakin kärjestä, johon kärjestä ![]() pääsee, etäisyys on
pääsee, etäisyys on ![]() särmää. On samantekevää, mikä suunta valitaan ensin – sopivia vaihtoehtoja on siis
särmää. On samantekevää, mikä suunta valitaan ensin – sopivia vaihtoehtoja on siis ![]() . Toisessa kärjessä on aivan sama, minne muurahainen jatkaa matkaansa, kunhan se ei palaa takaisin. Vaihtoehtoja on siis
. Toisessa kärjessä on aivan sama, minne muurahainen jatkaa matkaansa, kunhan se ei palaa takaisin. Vaihtoehtoja on siis ![]() . Kolmannesta kärjestä on yksi reitti kärkeen
. Kolmannesta kärjestä on yksi reitti kärkeen ![]() . Näin ollen suotuisia reittejä on
. Näin ollen suotuisia reittejä on ![]() .
.
Klassisen todennäköisyyden mukaan kysytty todennäköisyys on siis ![]()
No niin, tämä oli helppo. Nyt mars mars Muurahaisen vaikean juoksun pariin. Eiköhän tästä ainakin yksi tai kaksi vihjettä sen ratkaisemiseksi tullut.
