Monthly Archives: lokakuu 2015

0

Muurahaisen vaikea juoksu

|

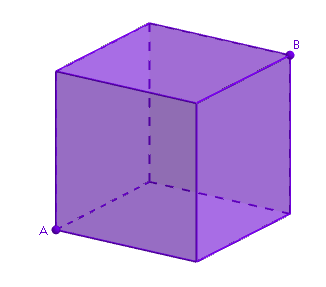
KuutioMuurahainen lähtee liikkeelle kuution kärjestä A ja etenee kuution särmiä pitkin. Kun muurahainen tulee johonkin kärkeen, se valitsee sattumanvaraisesti seuraavan särmän, jota pitkin se lähtee kulkemaan (se voi siis myös palata takaisin kohti kärkeä, josta se juuri lähti). Millä todennäköisyydellä muurahainen päätyy kärkeen B kuljettuaan täsmälleen seitsemän särmää?

(HUOM! Muurahaisen ei tarvitse olla seitsemännen särmän jälkeen ensimmäistä kertaa kärjessä B.)

Tämä ongelma on huomattavasti haastavampi kuin Muurahaisen helppo juoksu, joten suosittelen tutustumaan tähän vasta helpolla juoksulla lämmiteltyäsi.

Ratkaisu: Harva ongelma (edes tässä blogissa) on saanut minut innostumaan yhtä paljoa kuin tämä. Syy siihen on seuraavassa kerrassaan hurmaavassa tavassa ratkaista pulma.

Koska kaikki kulkureitit ovat yhtä todennäköisiä, päästään ongelman ratkaisussa soveltamaan klassista todennäköisyyttä. Kun liikutaan seitsemän särmää, ja jokaisessa kärjessä on kolme vaihtoehtoa seuraavaksi suunnaksi, on erilaisia kulkureittejä tuloperiaatteen nojalla 3^7=2187 kappaletta. Selvitetään seuraavaksi, kuinka moni näistä reiteistä on suotuisia tapauksia muurahaisellemme.

Olkoon piste A=(0,0,0) ja piste B=(1,1,1). Jokaisen särmän liikkuminen muuttaa täsmälleen yhtä pisteen kolmesta koordinaatista, nollasta ykköseksi tai ykkösestä nollaksi. Tavoitteemme olisi siis se, että kaikkia koordinaatteja olisi seitsemän särmän jälkeen muutettu pariton määrä kertoja. Tämä voidaan tehdä kahdella ja vain kahdella erilaisella tavalla:

  1. Yhtä koordinaattia muutetaan viidesti ja kahta muuta kerran.
  2. Kahta koordinaattia muutetaan kolmesti ja yhtä kerran.

Lasketaan sitten, montako erilaista reittiä tapauksiin 1 ja 2 sisältyy. Viidesti muutettava koordinaatti voidaan valita kolmella tavalla. Edelleen kombinatoriikkaa soveltaen viisi vaihtoa seitsemästä voidaan valita \binom{7}{5}=\frac{7!}{5!2!}=21 tavalla. Jäljelle jäävien koordinaattien vaihdoista ensimmäinen voidaan valita kahdesta jäljellä olevasta vaihtopaikasta, jolloin viimeiselle koordinaatin vaihdolle jää vain yksi paikka. Näin ollen tapaukselle 1 suotuisia reittejä on

    \[3\cdot\binom{7}{5}\cdot 2\cdot 1=126.\]

Vastaavaa päättelyä noudattaen tapaukseen 2 sisältyy 3\cdot\binom{7}{3}\cdot \binom{4}{3}\cdot 1=420 mahdollista reittiä. Koska tapaukset 1 ja 2 ovat erilliset, eli niihin ei sisälly samoja reittejä, on reittien kokonaismäärä 126+420=546 Näin ollen todennäköisyys sille, että seitsemännen särmän jälkeen ollaan kärjessä B on klassisen todennäköisyyden mukaan

    \[\frac{546}{2187}=\frac{182}{729}=0,2496\ldots\approx 0,25.\]

Tästäkin ongelmasta iso kiitos Thomas Poveylle, jonka pulmakirjaa Professor Povey’s Perplexing Problems olen nyt pari viikkoa iltaisin jatkuvasti selaillut. Kirjassa on kymmeniä tiukkoja matematiikan ja fysiikan tehtäviä, jotka on suunnattu korkeakouluopintojen kynnyksellä oleville ongelmanratkaisusta innostuneille opiskelijoille. Tai sitten heidän opettajilleen. Erittäin suositeltava opus.

PS. Eräs opiskelijani heitti suunnilleen välittömästi ongelman kuultuaan arvauksen, että vastaus ei varmaankaan ole \frac{1}{4}, mutta että se on sinnepäin. Aivan oikein. Parittomalla siirtomäärällä kuutiossa on vain neljä kärkeä, joissa muurahainen voi olla. Mitä suuremmaksi siirtojen määrä kasvaa – kunhan niitä on vain pariton määrä – sitä lähempänä todennäköisyys päätyä kärkeen B on arvoa \frac{1}{4}.

0

Muurahaisen helppo juoksu

|

KuutioMuurahainen lähtee liikkeelle kuution kärjestä A ja etenee kuution särmiä pitkin. Kun muurahainen tulee johonkin kärkeen, se valitsee sattumanvaraisesti seuraavan särmän, jota pitkin se lähtee kulkemaan (se voi siis myös palata takaisin kohti kärkeä, josta se juuri lähti). Millä todennäköisyydellä muurahainen päätyy kärkeen B täsmälleen kolme särmää kuljettuaan?

Ratkaisu: Jokaisessa kärjessä muurahaisella on kolme vaihtoehtoa seuraavalle suunnalle, joten erilaisia kolmen särmän reittejä on tuloperiaatteen mukaan 3\cdot 3\cdot 3=27.

Mietitään sitten, kuinka moni reiteistä vie kolmea särmää pitkin kärkeen B. Kärki A on ainoa kärki, josta etäisyys kärkeen B on 3 särmää. Kustakin kärjestä, johon kärjestä A pääsee, etäisyys on 2 särmää. On samantekevää, mikä suunta valitaan ensin – sopivia vaihtoehtoja on siis 3. Toisessa kärjessä on aivan sama, minne muurahainen jatkaa matkaansa, kunhan se ei palaa takaisin. Vaihtoehtoja on siis 2. Kolmannesta kärjestä on yksi reitti kärkeen B. Näin ollen suotuisia reittejä on 3\cdot 2\cdot 1=6.

Klassisen todennäköisyyden mukaan kysytty todennäköisyys on siis \frac{6}{27}=\frac{2}{9}.

No niin, tämä oli helppo. Nyt mars mars Muurahaisen vaikean juoksun pariin. Eiköhän tästä ainakin yksi tai kaksi vihjettä sen ratkaisemiseksi tullut.

6

Kaksi rahakuorta

|

Tämä ongelma liittyy oleellisesti kolmen rahakuoren pulmaan, joten suosittelen tutustumaan siihen ja sen ratkaisuun ensin. Luvassa on ensinäkemältä hämmästyttävä paradoksi.

Saat kirjekuoren, jossa on tietty määrä rahaa. Minulla on suljettu kirjekuori, jossa on joko kaksi kertaa enemmän rahaa kuin sinun kuoressasi tai vain puolet rahoistasi. Kannattaako sinun vaihtaa?

Päätellään kuten kolmen kuoren ongelmassa, että vaihtaminen kannattaa:

  1. Olkoon kuoressasi X euroa.
  2. Rahasumma X voi olla joko suurempi tai pienempi kuin toisen kuoren rahasumma.
  3. Toisen kuoren rahasumma on siis \frac{X}{2} todennäköisyydellä \frac{1}{2} tai 2X todennäköisyydellä \frac{1}{2}.
  4. Näin ollen rahasumman odotusarvoksi saadaan \frac{1}{2}\cdot \frac{X}{2}+\frac{1}{2}\cdot 2X=\frac{5}{4}X.

Uskomaton tulos! Tämä sotii vahvasti arkista järkeilyä vastaan. Onko vika päättelyssä vai arkijärjessä?

Ratkaisu: Tällä kerralla ongelma todella on päättelyssä, tarkemmin sanottuna kohdassa 3. Emme voi lähteä siitä, että toisessa kuoressa olisi 2X tai \frac{1}{2}X ja laskea odotusarvoa kuten kolmen kuoren ongelmassa. Tämä siksi, että ne molemmat eivät ole mahdollisia tapauksia.

Oikeaa päättelyä olisi todeta, että on kaksi rahakuorta, joissa on rahasummat X ja 2X, mutta emme tiedä, kumpi niistä on hallussamme. Nyt hallussamme olevan rahasumman odotusarvo on \frac{1}{2}\cdot X+\frac{1}{2}\cdot 2X=\frac{3}{2}X, mikä puolestaan tarkoittaa, että on yhdentekevää, vaihtaako vai ei. On yhtä todennäköistä, että hallussa on iso tai pieni rahasumma, eikä se vaihtamalla muutu.

Tämänkin pulman lähteenä oli Thomas Poveyn matematiikka- ja fysiikkaongelmia käsittelevä opus Professor Povey’s Perplexing Problems.

2

Kolme rahakuorta

|

Seuraava pulma on jälleen Thomas Poveyn peruja. Se on sukua kuuluisalle Monty Hallin ongelmalle, mutta siinä on oma pieni lisämausteensa.

Saat kirjekuoren, jossa on tietty summa rahaa. Tämän jälkeen näytän sinulle kaksi muuta kuorta, joista toisessa on kaksinkertainen rahasumma ja toisessa puolet kirjekuoresi rahasummasta. Suljen kaksi muuta kuorta ja sekoitan ne niin, ettei niistä voi mitenkään päätellä, kumpi oli kumpi. Nyt sinulla on kaksi vaihtoehtoa: voit joko pitää nykyisen kuoresi tai vaihtaa jompaan kumpaan toisista kuorista. Mitä sinun kannattaisi tehdä?

Ratkaisu: Tutkitaan ongelmaa odotusarvon käsitteen kautta. Odotusarvo tarkoittaa eräänlaista satunnaisilmiön jakauman keskiarvoa, jota laskettaessa satunnaismuuttujan arvot painottuvat niiden todennäköisyyksien suhteessa.

Olkoon nyt kirjekuoressasi oleva rahasumma X. Näin ollen kahdessa muussa kuoressa olevat rahasummat ovat 2X sekä \frac{1}{2}X. Nyt on kaksi mahdollista tapausta.

  1. Et vaihda kuoria. Tällöin saamasi rahasumman odotusarvo on varmasti X.
  2. Vaihdat. Nyt voit todennäköisyydellä \frac{1}{2} saada kuoren, jossa on 2X, ja samoin todennäköisyydellä \frac{1}{2} kuoren, jossa on \frac{1}{2}X. Saamasi rahasumman odotusarvo on nyt \frac{1}{2}\cdot 2X+\frac{1}{2}\cdot\frac{1}{2}X=\frac{5}{4}X.

Näin ollen vaihto kannattaa.

 

0

Kaarien rajaama ala

|

Sain viimein käsiini Thomas Poveyn pulmakirjan nimeltä Professor Povey’s Perplexing Problems (Oneworld Publications, 2015). Jo nopealla ensi silmäilyllä ja todella pintapuolisella selailulla kävi selväksi, että nyt on käsissä helmi. Poveyn mukaan kirjan ongelmat eivät vaadi mitään lukiotason matematiikkaa kummempia menetelmiä, mutta luovaa kykyä ongelmanratkaisuun kyllä kaivataan. Tässä yksi maistiainen kirjan sisällöstä. Näyttää ihan helpolta, mutta –

Neliön sivun pituus on 2a. Sen vastakkaisista kärjistä piirretään ympyränkaaret, joiden säteet ovat a ja 2a. Mikä on kaarien rajaaman alueen pinta-ala?Näyttökuva 2015-10-9 kello 18.39.21

 

 

2

Laskut sekaisin

|

Kiireinen yrittäjä lähettää kuudelle asiakkaalleen laskun ja sulkee ne kirjekuoriin. Äkkiä hän huomaa, että osoitetarrat unohtuivat kuorien päältä. Millä todennäköisyydellä hän saa sattumanvaraisesti lätkimistään tarroista täsmälleen viisi oikeisiin kuoriin?

Kirjuri Ezra (n. 700-l.) Kuvalähde: Wikimedia Commons/Public domain

Kirjuri Ezra (n. 700-l.) Kuvalähde: Wikimedia Commons/Public domain

Ratkaisu: Todennäköisyys on nolla. Jos viisi osoitetta menee oikein, myös kuudes menee.

0

Omenapora

|

Pitkän matematiikan syksyn 2015 ylioppilaskokeessa tehtävänä 7 kysyttiin seuraavaa:

Täysin pyöreän geenimanipuloidun omenan säde on 5,0 cm. Omenan läpi porataan sen keskeltä kulkeva reikä, jonka säde on 1,0 cm. Kuinka monta prosenttia omenan tilavuudesta tällöin häviää? Anna vastaus prosenttiyksikön kymmenesosan tarkkuudella.

Tehtävä on ihan hauska ja hyvä, mutta vielä hauskempi on tehtävän ilkeä äitipuoli. Jos olisin Martin Gardner, olisin kysynyt abiturienteilta näin:

Pallon muotoisen omenan läpi porataan kuusi senttimetriä pitkä reikä, joka kulkee pallon keskipisteen kautta. Kuinka suuri on jäljelle jäävän omenan tilavuus?

Kuva: Alan Levine/Flickr (CC BY 2.0)

Kuva: Alan Levine/Flickr (CC BY 2.0)

Ratkaisu:

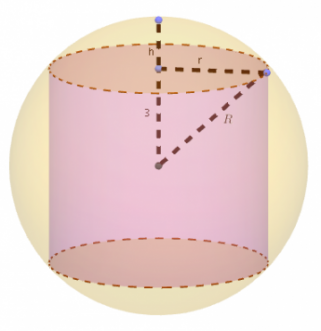
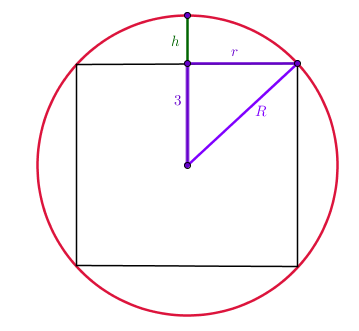
Lieriö pallossaPallo ja lieriö – poikkileikkaus

Omenapora leikkaa omenasta kappaleen, joka muodostuu suorasta ympyrälieriöstä, jonka korkeus on mainittu 6 cm, sekä kahdesta pallosegmentistä. Olkoon omenan säde R, lieriön säde r ja pallosegmentin korkeus h. Lieriö sijaitsee symmetrisesti omenan keskipisteen ylä- ja alapuolella, joten voimme piirtää oheisen poikkileikkauksen mukaisen kuvan. Nyt Pythagoraan lauseen nojalla R^2=3^2+r^2, eli r^2=R^2-3^2. Edelleen havaitaan, että pallosegmentin korkeus on h=R-3. Näistä huomioista saadaankin jo laskettua sekä lieriön että pallosegmentin tilavuudet:

    \[\begin{array}{rcl} V_l & = &\pi r^2\cdot 6=\pi(R^2-3^2)\cdot 6\\ & = & 6\pi R^2-54\pi;\\ V_{ps} & = & \pi h^2\left(R-\frac{h}{3}\right)\\ &=&\pi (R-3)^2\left(R-\frac{R-3}{3}\right)\\ & =&\frac{2}{3}\pi R^3-6\pi R^2+18\pi. \end{array}\]

Tämän jälkeen loppu on pelkkää sievennystä:

    \[\begin{array}{rcl} V_{omena} & =&V_{pallo}-V_l-2V_{ps}\\ &=&\frac{4}{3}\pi R^3-\left(6\pi R^2-54\pi\right)-2\left(\frac{2}{3}\pi R^3-6\pi R^2+18\pi\right)\\ &=&36\pi. \end{array}\]

Vastaus on siis – ehkä hieman yllättäen – omenan säteestä riippumaton vakio.

Jälkikirjoitus: Annoin tämän ongelman viime keväänä pohdittavaksi parille opiskelijalleni. Eräs heistä esitti ongelmaan sangen ketterän ratkaisun. Hän totesi, että pienentämällä reiän sädettä kohti nollaa on päädyttävä samaan ratkaisuun kuin missä muussa tapauksessa tahansa. Reiän ja pallosegmenttien hävitessä raja-arvona on pallo, jonka halkaisija on 6. Siispä jäljelle jäävä tilavuus on sama kuin 3-säteisen pallon, eli \displaystyle\frac{4}{3}\pi\cdot 3^3=36\pi. Ratkaisu on sinänsä ovela oikotie, mutta se perustuu ehkä vähän kyseenalaiseen lisäoletukseen: voimmeko tehtävänannon perusteella luotettavasti päätellä, että kyseessä on ongelma, johon on olemassa yksikäsitteinen ratkaisu?