Pyöreä kolikko pudotetaan sattumanvaraisesti suurelle shakkilaudalle. Shakkilaudan ruudun sivu on kaksinkertainen kolikon halkaisijaan verrattuna. Millä todennäköisyydellä kolikko putoaa sekä mustan että valkean ruudun päälle?
Tämä hauska pikku pulma tuli vastaan Alex Bellosin The Guardianissa pitämää pulmapalstaa selatessani. Hän puolestaan sanoi löytäneensä ongelman kirjasta, jolla on hieno nimi: Professor Povey’s Perplexing Problems. Tämä Thomas Poveyn kirja lähtikin heti tilaukseen. Pitäkää siis varanne jatkossakin, rakkaat pulmakulman lukijat!
Ratkaisu:
Tarkastellaan shakkilautaa, jonka ruudun sivun pituus on ![]() . Tällöin kolikon halkaisija on
. Tällöin kolikon halkaisija on ![]() , ja kolikkoja mahtuu kerralla yhden ruudun sisälle neljä. Tässä asetelmassa kolikkojen keskipisteet muodostavat neliön, jonka sivun pituus on
, ja kolikkoja mahtuu kerralla yhden ruudun sisälle neljä. Tässä asetelmassa kolikkojen keskipisteet muodostavat neliön, jonka sivun pituus on ![]() .
. 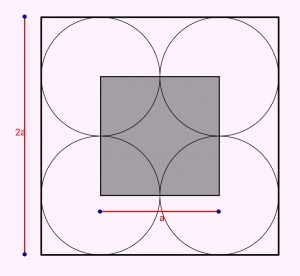
Jos nyt pudotamme kolikon shakkiruudulle, ei se ulotu toisen ruudun puolelle, mikäli sen keskipiste jää tummennetun neliön sisälle. Tämän tummennetun neliön ala on ![]() koko ruudun alasta, joten vastaus kysymykseen on tietenkin
koko ruudun alasta, joten vastaus kysymykseen on tietenkin ![]() .
.
