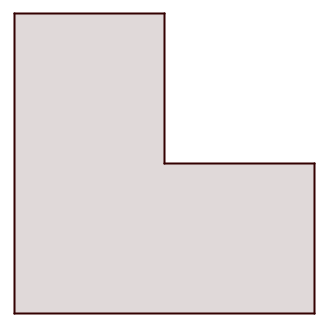
Tarkastellaan ensiksi kuviota, joka muodostuu, kun neliöstä leikataan oikeanpuoleinen yläneljännes pois. Pystytkö jakamaan sen neljäksi yhteneväksi (samankokoiseksi ja samanmuotoiseksi) kuvioksi?
Otetaan sitten sama neliö, mutta nyt leikkaamattomana. Pystytkö jakamaan sen viideksi yhteneväksi kuvioksi?
Tämä ongelma on vanha klassikko, josta minua muistutti matemaatikko James Grime Twitterissä. Grime on mainio esiintyjä, joka on poikennut Suomessakin kertoilemassa mm. Alan Turingista ja Enigma-salakirjoituslaitteen murtamisesta.
Neliö, josta on yksi neljännes leikattu, voidaan jakaa neljäksi yhteneväksi kuvioksi näin:
Toinen kysymys johtikin sitten jälleen puujalkavitsiosastolle. Sama neliö voidaan jakaa viiteen yhtenevään palaan esimerkiksi näin:


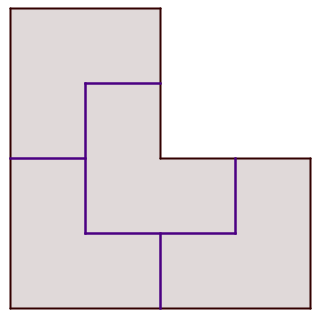

Kuvio on samanmuotoinen kuin lähtökuvio. Ensimmäinen vasempaan alanurkkaan samoin päin kuin lähtökuvio, toinen vasempaan ylänurkkaan 90 astetta oikealle kierrettynä, kolmas oikeaan alanurkkaan 90 astetta vasemmalle kierrettynä ja neljäs tulee samoin päin kuin lähtökuvio ensimmäisen sisäkulmaan.
Neliö voidaan jakaa tylsästi viideksi samanlevyikseksi soiroksi.